С бесконечными пределами интегрирования

Теоремы о сходимости несобственных интегралов

В практических задачах часто достаточно определить только сходимость интеграла, а не его величину.

Теорема 5.2. Если непрерывные функци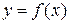и и 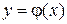на промежутке 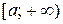удовлетворяют соотношению 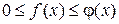, то если 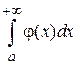сходится, то и 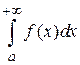сходится; если же 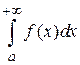расходится, то 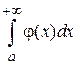расходится.

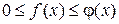
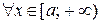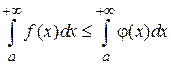Д о к а з а т е л ь с т в о. По свойству 5 определенных интегралов, если , то . Если 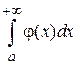сходится, т. е. существует конечный предел 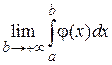, то интеграл 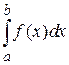ограничен. Ввиду того, что при возрастании b увеличивается интервал интегрирования и подынтегральная функция , то 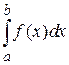монотонно возрастает и, следовательно, имеет предел .

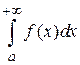Теперь обоснуем, что если 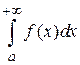расходится, то 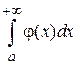расходится. От противного. Предположим, что интеграл 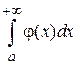сходится. Тогда по первому утверждению теоремы должен сходиться и интеграл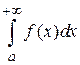. В этом и состоит противоречие.

Пример 5.6. Исследовать сходимость интеграла .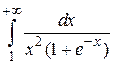

Для использования теоремы 5.2 основная трудность состоит в том, чтобы решить, какую функцию надо подбирать 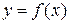или 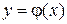, т. е. что мы хотим доказать, сходится интеграл или расходится. В данном примере, очевидно, . 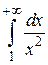сходится, так как степень 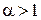(см. пример 5.5). Следовательно, исходный интеграл сходится.

Пример 5.7. Исследовать сходимость интеграла .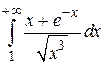

Подбираем функцию , .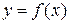

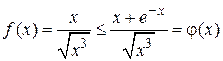
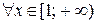Интеграл 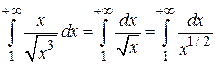расходится, так как 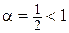(см. пример 5.5). Следовательно, исходный интеграл расходится.

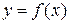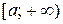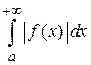Теорема 5.3. Если функция непрерывна на промежутке и сходится, то также сходится .

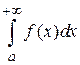Если сходятся одновременно интегралы 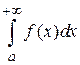и 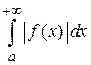, то интеграл 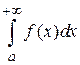называется абсолютно сходящимся.

Д о к а з а т е л ь с т в о. Для любого значения х из промежутка 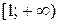справедливо неравенство 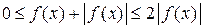. На основании свойства 5 для определенных интегралов 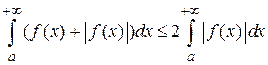. Так как по условию теоремы интеграл от функции 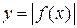сходится, то также сходится (по теореме 5.2) . Следовательно, сходится разность интегралов .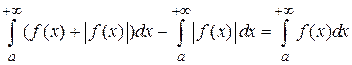

Пример 5.8. Исследовать сходимость интеграла .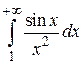

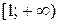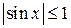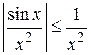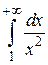Для любых значений х, принадлежащих промежутку , справедливы неравенства и . сходится, так как степень (см. пример 5.5). На основании теоремы 5.2 интеграл 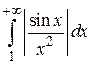сходится. На основании теоремы 5.3 интеграл 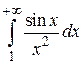сходится абсолютно.

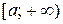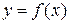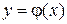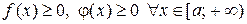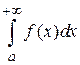Теорема 5.4. Если на промежутке для непрерывных неотрицательных функции и (), существует конечный предел отношения функций , неравный нулю, то оба интеграла от этих функций и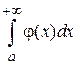либо сходятся, либо расходятся одновременно.

Д о к а з а т е л ь с т в о. Пусть 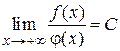, , 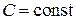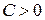. По определению предела .

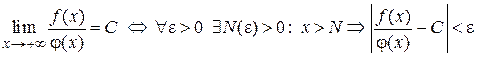Здесь e сколь угодно малое положительное число.

Справедливы соотношения

.

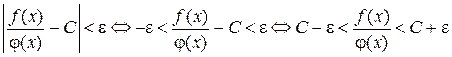Так как 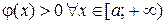, , 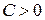а e сколь угодно малое число, то 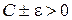и справедливо

.

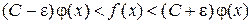Используем это неравенство и теорему 5.2. Если интеграл 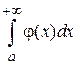сходится, то интеграл 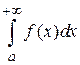также сходится. И наоборот, если интеграл 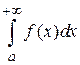расходится, то и интеграл 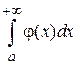расходится.

Пример 5.9. Исследовать на сходимость интеграл .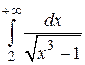

Подынтегральную функцию 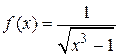сравним с функцией 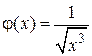. Находим предел отношения функций

.

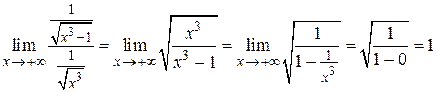Предел является конечной величиной, поэтому интегралы от этих функций сходятся или расходятся одновременно. Интеграл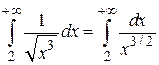сходится, так как степень х в подынтегральной функции 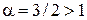(см. пример 5.5). Следовательно, исходный интеграл также сходится.

Пример 5.10. Исследовать на сходимость интеграл .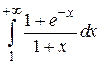

Найдем предел отношения функци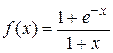й и .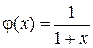

.

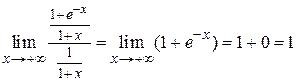Предел является конечной величиной, поэтому интегралы от этих функций сходятся или расходятся одновременно.

Интеграл 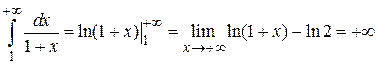расходится.

Следовательно, исходный интеграл также расходится.

Дата добавления: 2014-01-11