
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ чувствительности схем
|
|
|
|
Нестабильность схемных параметров (схемных функций, параметров частотных и временных характеристик, отдельных токов и напряжений и т.д.) оценивается их чувствительностью к вариациям значений параметров компонентов схемы.
Чувствительность (относительная) определяется как отношение относительного изменения схемного параметра (схемной функции и др.) к относительному изменению i одного из параметров компоненты схемы:
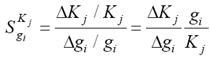 . (7.1)
. (7.1)
При малых изменениях gi, когда можно считать, что 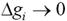 и значит
и значит  , можно перейти к дифференциальной, или логарифмической, форме записи чувствительности:
, можно перейти к дифференциальной, или логарифмической, форме записи чувствительности:
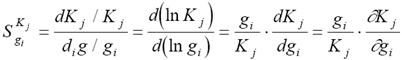 . (7.2)
. (7.2)
Из последнего выражения ясен способ вычисления чувствительности по известному выражению для 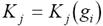 . Он основан на вычислении частных производных от схемных параметров (схемных функций и др.).
. Он основан на вычислении частных производных от схемных параметров (схемных функций и др.).
Для чувствительностей схемных параметров характерны некоторые соотношения, которые имеют важное практическое значение. Так:
1. Сумма чувствительностей некоторого схемного параметра к вариациям параметров всех компонентов пассивной схемы является величиной постоянной во всем диапазоне частот и остается инвариантной при любых эквивалентных преобразованиях схемы, т. е.
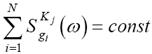 . (7.3)
. (7.3)
Указанное свойство инвариантности, как видим, остается справедливым и для активных схем с зависимыми источниками тока, управляемыми напряжением, или зависимыми источниками напряжения, управляемыми током. Тогда их управляющие параметры имеют размерность проводимости или сопротивления.
2. Сумма чувствительностей схемной функции к вариациям параметров всех реактивных компонентов (L, C) инвариантна для всех схем, описываемых такой же схемной функцией, и равна чувствительности той же схемной функции к вариациям комплексной переменной (комплексной частоты) p:
|
|
|
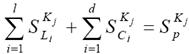 , (7.4)
, (7.4)
где l - число индуктивных компонентов в схеме;
d - число емкостных компонентов в схеме;
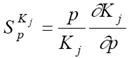 . (7.5)
. (7.5)
Для определения чувствительности модуля и фазы передаточной функции к изменениям варьируемого параметра запишем следующее представление функции чувствительности:
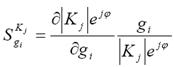 (7.6)
(7.6)
или
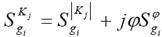 . (7.7)
. (7.7)
Тогда чувствительность модуля передаточной функции к изменениям варьируемого параметра определится:
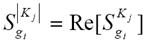 , (7.8)
, (7.8)
а чувствительность фазы передаточной функции к изменениям варьируемого параметра определится:
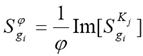 . (7.9)
. (7.9)
Абсолютная чувствительность схемной функции y к параметру схемы 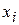 определяется как
определяется как
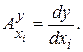 (7.10)
(7.10)
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 699; Нарушение авторских прав?; Мы поможем в написании вашей работы!