Параметрической цепи

Импульсная характеристика и передаточная функция

Для определения импульсной характеристики g (t,τ), где τ - время воздействия, t - время появления и действия отклика, непосредственно по заданным параметрам цепи необходимо использовать дифференциальное уравнение цепи.

Чтобы проанализировать методику нахождения g (t,τ), рассмотрим простую цепь, описываемую уравнением первого порядка:

где f (t) - воздействие, y (t) - отклик.

По определению, импульсная характеристика является откликом цепи на одиночный дельта-импульс δ(t -τ), подаваемый на вход в момент t =τ. Из этого определения следует, что если в правой части уравнения положить f (t)=δ(t -τ), то в левой части можно принять y (t)= g (t,t).

Таким образом, приходим к уравнению

.

Так как правая часть этого уравнения равна нулю всюду, кроме точки t =τ, функцию g (t) можно искать в виде решения однородного дифференциального уравнения:

при начальных условиях, вытекающих из предыдущего уравнения, а также из условия, что к моменту приложения импульса δ(t -τ) в цепи отсутствуют токи и напряжения.

В последнем уравнении переменные разделяются:

Откуда

где - значения импульсной характеристики в момент воздействия.

Для определения начального значения вернемся к исходному уравнению. Из него следует, что в точке функция g (t) должна совершить скачок на величину 1/ а ₁(τ), поскольку только при этом условии первое слагаемое в исходном уравнении a ₁(t)[ dg / dt ] может образовывать дельта-функцию δ(t -τ).

Так как при , то в момент

.

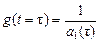Заменяя неопределенный интеграл определенным с переменным верхним пределом интегрирования, получаем соотношения для определения импульсной характеристики:

.

Зная импульсную характеристику, нетрудно определить передаточную функцию линейной параметрической цепи, поскольку обе оси связаны парой преобразования Фурье:

где a = t -τ - задержка сигнала. Функция g ₁(t, a) получается из функции заменой τ= t-a.

Наряду с последним выражением, можно получить еще одно определение передаточной функции, в котором импульсная характеристика g ₁(t, a) не фигурирует. Для этого используем обратное преобразование Фурье для отклика S _ВЫХ(t):

.

Для случая, когда входной сигнал является гармоническим колебанием, S (t)=cosω_0 t. Соответствующий S (t) аналитический сигнал есть .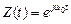

Спектральная плоскость этого сигнала

Подставляя вместо в последнюю формулу, получаем

.

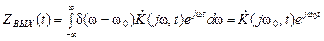Отсюда находим:

.

Здесь Z _ВЫХ(t) - аналитический сигнал, соответствующий выходному сигналу S _ВЫХ(t).

Таким образом, выходной сигнал при гармоническом воздействии

определяется так же, как и для любых других линейных цепей.

Если передаточная функция K (j ω₀, t) изменяется во времени по периодическому закону с основной частотой Ω, то ее можно представить в виде ряда Фурье:

где - не зависящие от времени коэффициенты, в общем случае комплексные, которые можно трактовать как передаточные функции некоторых четырехполюсников с постоянными параметрами.

Произведение

можно рассматривать как передаточную функцию каскадного (последовательного) соединения двух четырехполюсников: одного с передаточной функцией , не зависящей от времени, и второго с передаточной функцией , изменяющейся во времени, но не зависящей от частоты ω₀ входного сигнала.

Основываясь на последнем выражении, любую параметрическую цепь с периодически изменяющимися параметрами можно представить в виде следующей эквивалентной схемы:

Откуда понятен процесс образования новых частот в спектре выходного сигнала.

Аналитический сигнал на выходе будет равен

где φ₀, φ₁, φ₂… - фазовые характеристики четырехполюсников .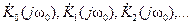

Переходя к вещественному сигналу на выходе, получаем

Этот результат указывает на следующее свойство цепи с переменными параметрами: при изменении передаточной функции по любому сложному, но периодическому закону с основной частотой

Ω, гармонический входной сигнал с частотой ω₀ образует на выходе цепи спектр, содержащий частоты ω₀, ω₀±Ω, ω₀±2Ω и т. д.

Если на вход цепи подается сложный сигнал, то все сказанное выше относится к каждой из частот ω и к входному спектру. Разумеется, что в линейной параметрической цепи никакого взаимодействия между отдельными компонентами входного спектра не существует (принцип суперпозиции) и на выходе цепи не возникает частот вида n _ω₁± m ω₂ где ω₁ и ω₂ - различные частоты входного сигнала.

Дата добавления: 2014-11-06