Выборка и её характеристики

Любая группа однородных данных, собранных при измерении параметров – это с т а т и с т и ч е с к а я с о в о к у п н о с т ь или более кратко: в ы б о р к а, т.е. часть генеральной совокупности.

Каждая выборка характеризуется показателями (оценками) нахождения центра распределения данных в группе и характеристиками рассеяния этих данных.

а) Характеристики положения центра группирования данных

Таких характеристик несколько:

- Выборочное среднее арифметическое - это сумма всех данных,

делённая на их число: 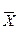= Σ Х _i / n, где 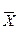– среднее, Х _i – каждое значение в группе, Σ – знак суммирования, а n – объём выборки.

Например, получены девять чисел: 6, 7, 3, 5, 8, 4, 9, 7, 5. Для них среднее арифметическое 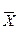= 6.

Выборочное среднеарифметическое – наиболее широко используемая мера центра распределения группы данных. Достоинства этой меры – это «центр тяжести» всех данных, в ней используются все данные, не нужна их сортировка. Недостатки – резко выделяющиеся значения иногда портят картину, часто требуется значительное время для расчёта, часто среднее не совпадает ни с одним из фактических значений.

- Мода - это то значение, которое встречается в группе данных

наиболее часто.

Например, из девяти чисел 6, 7, 3, 5, 8, 4, 5, 7, 5 модой будет = 5.

Для групп данных может существовать более чем одна мода. Достоинства этой меры – не надо ни вычислять, ни сортировать данные, резко выделяющиеся значения не влияют на результат, это одно из фактических значений, его можно отыскать визуально на графике распределения данных. Недостаток – данные могут и не иметь моды.

- Медиана - это срединное значение данных упорядоченных

(или ранжированных) по возрастанию или по убыванию. Для чётного числа данных медиана – среднее из двух ближайших к центру значений.

Например, из десяти чисел 2, 2, 3, 3, 5, 7, 7, 7, 8, 8 медианой будет число (или ) = 6.

Достоинства медианы – позволяет представить, где расположена бо'льшая часть, требуется относительно мало вычислений. Недостатки – данные надо сортировать, используются не все данные. Резко выделяющиеся значения могут быть существенными.

б) Характеристики изменчивости (рассеяния) данных в группе

Наиболее используемы в практике четыре характеристики:

- Размах - в группе данных R – это разность между наибольшим и наименьшим значениями: R = Х _max – Х _min.

Например, из девяти чисел 5, 3, 7, 9, 8, 5, 4, 5, 8 - R = 9 – 3 = 6.

Размах, как меру рассеяния, используют для малых выборок.

- Выборочная дисперсия - σ - равна сумме квадратов отклоне-

ний от среднего, делённой на объём выборки.

Расчётная формула: σ = Σ (Х _ί – 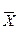) ² / n.

При решении практических задач часто используется исправленная выборочная дисперсия:

S² = Σ (Х _ί – 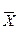) ² / (n – 1).

Для предыдущей группы значений σ = 4,25.

Исправленное выборочное среднее квадратическое отклонение:

.

Это отклонение называют также стандартным.

Дисперсия наилучшим образом характеризует разбросанность случайной величины.

К дисперсии применимо правило аддитивности, т.е. дисперсия суммы или разности выборок равна сумме дисперсий каждой выборки (рис. 1.)

Z =X + Y Z = X – Y

μ _z = μ _x + μ _y μ _z = μ _x – μ _y

σ _z = σ _x + σ _y (S ²_z = S ²_x + S ²_y) σ _z = σ _x + σ _y (S ²_z = S ²_x + S ²_y)

Рис. 4.

Соотношение средних и дисперсий для суммы и разности выборок

Дисперсия равна квадрату стандартного отклонения: σ = S ².

Для генеральной совокупности в знаменателе приведённых формул берётся n, а для выборки: n – 1 (когда оценивание надо сделать по выборке для генеральной совокупности).

- Коэффициент вариации - равен стандартному отклонению, делённому на среднее, и выражается в процентах: v = S ּ 100 / , %.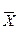

Дата добавления: 2014-10-15