Сравнение выборок

При предварительном анализе данных наблюдений часто возникает необходимость сравнения двух или нескольких выборок данных, полученных в относительно разных условиях, чтобы решить одинаковы ли они, принадлежат ли одной генеральной совокупности, и тогда эти выборки при необходимости можно объединять для последующего анализа более мощного массива данных; или же выборки неодинаковы, а значит разница между ними не случайна и выборки не могут быть объединены.

Сравнивают выборки по их средним значениям [ 2 ]. Однако это сравнение производится по-разному в зависимости от того, как соотносятся между собой дисперсии этих выборок. Поэтому вначале определяют равны или не равны эти дисперсии.

а) Сравнение двух дисперсий

В качестве характеристики проверки гипотезы о равенстве дисперсий используется частное несмещённых оценок дисперсий генеральной совокупности:

,

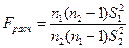где в числителе должна быть бо'льшая из двух оценок рассеяния (для того, чтобы значение F_расч всегда было больше 1).

Доказано, что характеристика F имеет F-распределение с (n ₁ – 1) и (n ₂ – 1) степенями свободы. Критическая область для проверяемой гипотезы при уровне значимости α является односторонней и определяется соотношением F _расч и F _α. Величину F _α определяем при уровне значимости α = 0,05 или α = 0,01 из Приложения 1.

Если F _расч < F _α, значит дисперсии равны (при этом не значит, чтобы были одинаковыми их численные выражения); если же F _расч > F _α, то дисперсии считаются не равными, и значит разница между выборками не случайна, и существуют какие-то для этого причины.

Например, сравним работу за месяц двух смен цеха флоут-стекла по производительности (съёму) процесса. Показатели работы смены № 1 – 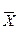₁ = 101,29 т/сут; S²₁ = 0,0729 т/сут; n ₁ = 16 смен; соответственно у смены № 2 - 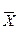₂ = 101,69; S²₂ = 0,1369; n ₂ = 14. Каждую группу можем считать случайной выборкой из нормальной генеральной совокупности.

По таблице F-распределения найдём при уровне значимости α = 0,05 и 16-1=15 и 14-1=13 степенях свободы F _0,05 = 2,53. Подсчитаем величину F _расч = 14ּ15ּ0,1369 / 16ּ13ּ0,0729 = 1,896. Поскольку F _расч < F _0.05, то делаем вывод: существенной разницы между дисперсиями генеральных совокупностей не обнаружено и, следовательно, для сравнения средних арифметических можно применить t-критерий

б) Сравнение среднеарифметических при равных дисперсиях.

В качестве характеристики сравнения рассчитывают величину

.

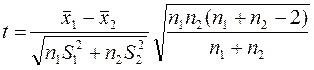Выборки считаются равными, если расчётная величина t оказывается больше, чем (- t _α), и меньше, чем (t _α), т.е. находится внутри диапазона: - t _α < t _расч < t _α.

Величина t _α находится по таблице для t – распределения (см. Приложение 2) при уровне значимости α и числе степеней свободы

n ₁ + n ₂ – 2.

Продолжим сравнение выборок из предыдущего примера. По таблице t-распределения при α = 0,05 и 16 + 14 – 2 = 28 степенях свободы

t _0.05 = 2,048. Следовательно, критическая область определяется t < -2,048 и t >2,048. На основании данных выборок рассчитаем величину характеристики 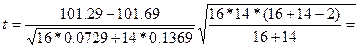-1,353. Поскольку эта величина попадает в критическую область (t = -1,353 < -2,048), значит сравниваемые выборки равны по своим средним арифметическим, разница между ними случайна и причины её не существенны.

в) Сравнение среднеарифметических при неравных дисперсиях.

При неравных дисперсиях среднеарифметические двух выборок сравнивают способом, также основанном на t – распределении, для которого двусторонняя симметричная критическая область определяется следующим образом.

Сначала рассчитывают величину t^' по формуле:

,

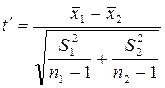которую сравнивают с величиной t", определяющей критическую область и рассчитываемой по формуле:

,

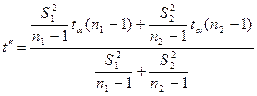где t _α (n ₁ – 1) – значение при n ₁ – 1 степенях свободы и уровне значимо-

сти α; t _α (n ₂ – 1) – значение при n ₂ – 1 степенях свобо-

ды и уровне значимости α. Эти значения находят в таб-

лице (см. Приложение 2).

В результате, если расчётная величина t^' < t^", то с полным основанием можно говорить о равенстве сравниваемых среднеарифметических.

В качестве примера сравним выработки листового стекла марки М-1 дневной (с 8-00 до 20-00 час) и ночной (с 20-00 до 8-00 час) смен в течении месяца. Параметр выражается в процентах полученного сортового стекла от сформованного. Характеристики работы дневной смены: 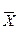₁= 48,35 %; S²₁ = 289; n ₁ = 31; соответственно у ночной - 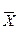₂ = 50,63 %; S²₂ = 150; n ₂ = 31.

Сначала сравним выборки по дисперсиям. По таблице F-распреде –

ления находим при уровне значимости α = 0,05 и 31-1=30 и 31-1=30 степенях свободы F _0,05 = 1,84. F _расч = 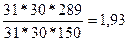. Поскольку F _расч > F _α , то дисперсии считаются неравными и сравнение средних арифметических производят по приближённому t- критерию.

По таблице t – распределения при 5%-ном уровне значимости t _0,05 для обоих выборок одинакова и равна 2,042. Определим критическую область:

t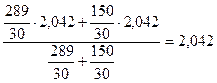^" = , а t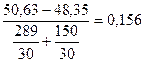^' = , то есть

t' < t" и значит средние арифметические сравниваемых выборок одинаковы.

Общий вывод: хотя в дневную смену есть причины для большей вариации технологического процесса, в среднем за данный месяц практически не отстала от ночной смены.

Примером анализа работы цеха можно взять сравнение выборок результатов работы смен и бригад (пример 4 из «Практикума»).

Сравнение результатов работы бригад показывает

Бригада	Ср. знач. съёма, %	Станд.отклон.
	71.286	9.619
	69.8	17.827
	63.344	19.772
	68.714	16,504

что хуже всех работает 3 бригада.

Среди других версий была сделана попытка оценить, каковы результаты работы 3 бригады после приёма смены от 1, 2 и 4 бригад. В нижеприведённой таблице представлены данные работы цеха за 2 месяца:

После 1 бр.			20,5						Сред.
После 2 бр.									70,2
После 4 бр.									65,2

Таким образом, 3 бригада работает хуже после 1 бригады. Причины этого следует искать дальше, в том числе в социальной сфере.

Дата добавления: 2014-10-15