Комбинаторика и бином Ньютона

Тема №4

Правило произведения. Пусть элемент х₁ строки (х₁, х₂, …, х_k) можно выбрать n₁ способами; после каждого выбора х₁ элемент х₂ можно выбрать n₂ способами; после выборов х₁ и х₂ элемент х₃ можно выбрать n₃ способами и т.д.; после выборов х₁, х₂, …, х_k-1 элемент х_k можно выбрать n_k способами. Тогда строку (х₁, х₂, …, х_k) можно образовать n₁ × n₂ × … × n_k способами.

Пример 1. Сколькими способами можно выбрать четырехзначное число, все цифры которого различны?

Решение. Каждому четырехзначному числу можно поставить во взаимно однозначное соответствие строку (х₁, х₂, х₃, х₄), где х₁, х₂, х₃, х₄ – соответственно 1, 2, 3 и 4-я цифры. Элемент х₁ этой строки можно выбрать 9 способами (любую из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9); элемент х₂ можно выбрать также 9 способами (теперь можно использовать и цифру 0, но первую выбранную цифру повторить нельзя); элемент х₃ можно выбрать 8 способами (уже выбранные первые две цифры повторить нельзя); наконец, элемент х₄ можно выбрать 7 способами. Согласно правилу произведения искомое число способов выбора четырехзначного числа с различными цифрами равно: 9 × 9 × 8 × 7 = 4536.

Размещения с повторениями. Пусть Х – множество, состоящее из n элементов (n-членное множество). Тогда любая строка длиной k, составленная из элементов множества Х, называется размещением с повторениями из n элементов по k.

Число всех размещений с повторениями из n элементов по k равно n^k.

Пример 2. Сколькими способами можно выбрать четырехзначное число, в десятичной записи которого нет нуля?

Решение. Четырехзначные числа указанного вида можно рассматривать как строки длиной 4, составленные из элементов множества Х = {1, 2, 3, 4, 5, 6, 7, 8, 9}, т.е. как размещения с повторениями из 9 элементов по 4. Следовательно, искомое число способов равно: 9⁴ = 6561.

Размещения без повторений. Перестановки. Пусть Х по-прежнему n -членное множество. Тогда любая строка длиной k, составленная из различных элементов множества Х, называется размещением без повторений из n элементов по k. Число всех таких размещений обозначается 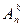и равно:

.

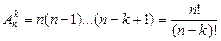В случае, когда k = n, размещения без повторений называются перестановками из n элементов. Число всех перестановок из n элементов обозначается P_n и равно:

P_n = = n!.

Пример 3. 10 спортсменов разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами?

Решение. Предположим, что спортсмены пронумерованы числами от 1 до 10 и х₁, х₂, х₃ – номера спортсменов, получивших золотую, серебряную и бронзовую медали. Каждому такому распределению медалей соответствует строка (х₁, х₂, х₃), состоящая из различных чисел (номеров спортсменов). Обратно каждой строке (х₁, х₂, х₃) соответствует способ распределения медалей. Следовательно, число способов распределения медалей равно числу размещений без повторений из 10 элементов по 3, т.е.

Сочетания и бином Ньютона. Всякое k -членное подмножество n-членного множества называется сочетанием из n элементов по k.

Число различных сочетаний из n элементов по k обозначается 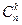. Справедлива формула

.

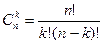Числа , , 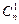,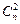…,,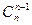 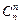являются коэффициентами в разложении бинома Ньютона:

(a + b) ⁿ = 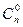a⁰ bⁿ + 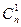a b^n-1 + … + 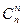aⁿ b⁰.

Пример 4. Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?

Решение. Очевидно, команда из 6 человек является 6-членным подмножеством 10-членного множества, т.е. сочетанием из 10 элементов по 6. Следовательно, искомое число способов равно

Размещения данного состава. Полиномиальная формула. Размещением данного состава (k₁, k₂,…, k_m) из элементов m -членного множества Х = { x₁, x₂,…, x_m } называется всякая строка длинной k₁ + k₂ + … + k_m = n, составленная из элементов множества Х, так, что элемент х₁ повторяется k₁ раз, элемент x₂ – k₂ раз и т.д., элемент x_m – k_m раз. Например, если Х= { x₁, x₂,x₃ }, то (x₁, x₂, x₂, х₁, х₁) есть размещение состава (3,2,0).

Количество различных размещений заданного состава (k₁, k₂,…, k_m) обозначается А(k₁, k₂,…, k_m) и равно:

.

Следующая формула, обобщающая формулу бинома Ньютона, называется полиномиальной:

,

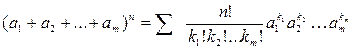где суммирование проводится по всевозможным наборам целых неотрицательных чисел k₁, k₂,…, k_m, для которых k₁ + k₂ + … + k_m = n.

Пример 5. Сколькими способами можно поставить на книжной полке 3 экземпляра учебника по алгебре, 2 экземпляра учебника по геометрии и один экземпляр учебника по математическому анализу?

Решение. Очевидно, всякой расстановке указанных учебников взаимно однозначно соответствует строка длиной 3 + 2 + 1 = 6 состава (3, 2,1). Следовательно, искомое число способов равно числу размещений состава (3, 2, 1).т.е.

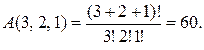
Пример 6. Вычислите (1 + х + х²)³.

Решение. По полиномиальной формуле имеем:

,

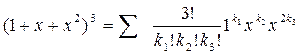где суммирование производится по всем наборам неотрицательных целых чисел k₁, k₂, k₃, для которых k₁ + k₂ + k₃ = 3. Выпишем все такие наборы: (0,0,3), (0,3,0), (3,0,0), (0,1,2), (1,2,0), (2,0,1), (1,0,2), (0,2,1), (2,1,0), (1,1,1). Теперь находим:

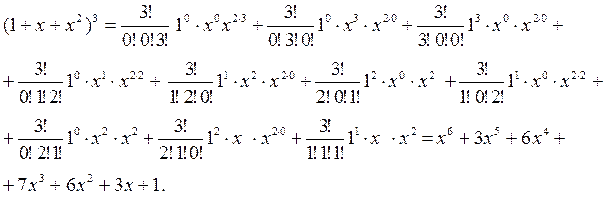
Контрольное задание №4

1. Имеется 5 видов конвертов без марок и 4 вида марок одинаковой стоимости. Сколькими способами можно выбрать конверт с маркой для посылки письма?

2 Сколько словарей надо издать, чтобы можно было непосредственно выполнить переводы с любого из 5 языков: русского, английского, французского, немецкого, итальянского – на любой другой из этих 5 языков?

3 У одного студента 5 книг, у другого – 9. Все книги различные. Сколькими способами студенты могут произвести обмен: а) одной книги на книгу? 2 книги на 2 книги?

4. На вершину горы ведут 5 тропинок. Сколькими способами турист может подняться в гору и потом спуститься с нее? Решите эту задачу с дополнительным условием: подъем и спуск должны происходить по разным тропинкам.

5. Сколькими способами на шахматной доске можно указать: а) 2 клетки? б) 2 клетки одного цвета? в) 2 клетки разного цвета?

6. Имеются 3 письма, каждое из которых можно послать по 6 различным адресам. Сколькими способами можно осуществить рассылку писем, если: а) никакие 2 письма не посылать по одному адресу; б) по одному можно адресу посылать более одного письма.

7. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при условии, что все они должны ехать в различных вагонах?

8. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых состоит не более чем из 3 цифр. Сколько таких чисел можно составить, если: а) повторение цифр в числах не разрешается; б) разрешается повторение цифр?

9. Сколькими способами 3 различных подарка А, В и С можно сделать каким-то 3 из 15 лиц, если: а) никто не должен получать более одного подарка; б) подарок А должно получить определенное лицо?

10. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

Дата добавления: 2014-10-22