Программирования

СПЕЦИАЛЬНЫЕ ЗАДАЧИ ЛИНЕЙНОГО

3.1. Транспортная задача (задача оптимального планирования перевозок груза)

Имеется m пунктов отправления (производства, поставщиков): А₁,..., А_m, в которых сосредоточены запасы некоего однородного груза в объемах a₁,..., а_m соответственно. Величины a_i определяют максимально возможные размеры вывоза груза с пунктов отправления. Суммарный запас груза поставщиков составляет .

Кроме того, имеется n пунктов назначения (потребления): B₁..., В_n, которые подали заявки на поставку груза в объемах b₁,..., b_n соответственно. Величины b_j определяют максимально возможные размеры ввоза груза в пункты назначения. Суммарная величина заявок составляет 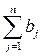. Стоимость перевозки 1 ед. груза от поставщика А_i к потребителю B_j – с_ij ден. ед. (транспортный тариф).

Требуется разработать оптимальный план перевозок таким образом, чтобы общая стоимость всех перевозок груза была минимальной при условии, что весь груз от поставщиков будет вывезен и все заявки потребителей удовлетворены.

В общем виде модель задачи оптимального планирования перевозок груза можно записать следующим образом:

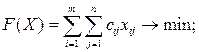(3.1)

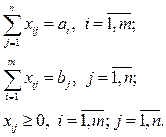(3.2)

где х_ij - количество однородного груза, перевозимого от поставщика A_i к потребителю B_j, .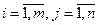

Таким образом, необходимо составить такой план перевозки груза, при котором целевая функция (3.1) принимала бы наименьшее значение и выполнялись бы условия (3.2).

Любое неотрицательное решение системы ограничений (3.2), определяемое матрицей Х =(х_ij), называется допустимым планом транспортной задачи. Допустимый план транспортной задачи, имеющий не более n + m- 1 отличных от 0 величин x_ij, называется опорным. Если в опорном плане число отличных от 0 компонент равно в точности n + m- 1, то план является невырожденным; если меньше этого числа, то план является вырожденным.

Условия транспортной задачи можно записать в виде распределительной таблицы (табл. 3.1).

Таблица 3.1

	Bj	B1	B2	…	Bn
Ai		b1	b2	…	bn
A1	a1	c11 x11	c12 x12	…	c1n x1n
A2	a2	c21 x21	c22 x22	…	c2n x2n
…	…	…	…	…	…
Am	am	cm1 xm1	cm2 xm2	…	cmn xmn

В моделях оптимального планирования перевозок груза должно выполняться балансовое равенство:

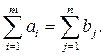(3.3)

Равенство (3.3) означает, что суммарный запас груза должен равняться суммарным потребностям. Модели, в которых выполняется балансовое равенство, называются закрытыми, в которых не выполняется - открытыми.

Уравнение баланса (3.3) выступает обязательным условием решения закрытой транспортной задачи; поэтому, когда в исходных условиях дана открытая задача, ее необходимо привести к закрытой форме.

Транспортные задачи могут решаться симплексным методом, однако перечисленные особенности позволяют применять для транспортных задач более простые методы решения.

Наиболее распространенным графо-аналитическим методом решения транспортных задач является метод потенциалов.

Алгоритм решения транспортных задач методом потенциалов

Шаг 1. Проверка балансового равенства (3.3).

Шаг 2. Разработка исходного опорного плана (опорного решения). Существуют два метода построения исходного опорного плана:

1) Метод северо-западного угла. Заполнение таблицы начинается с левой верхней ячейки, куда дается максимально возможная поставка. Объем поставки выбирается так, чтобы полностью закрыть либо потребность по столбцу b_j либо запас по строке а_i, т.е. в качестве х_ij выбирается минимум между запасами груза на первом складе и потребностями в грузе у первого потребителя: х₁₁ =min(a₁; b₁). Дальнейшее заполнение таблицы происходит слева направо, сверху вниз;

2) Метод наименьшего тарифа. Заполнение таблицы начинается с ячейки с наименьшим тарифом. Если таких ячеек несколько, то заполняется та, у которой объем перевозок больше. Объем поставки определяется так же, как и в методе северо-западного угла. Заполнив первую ячейку, среди оставшихся ячеек снова выбираем ячейку с наименьшим тарифом и т.д.

Если транспортная задача является открытой и введены фиктивные поставщики или фиктивные потребители, то распределение осуществляется сначала для действительных поставщиков и потребителей.

Шаг 3. Проверка вырожденности плана. Если число занятых ячеек в опорном плане меньше, чем m + n -1, т.е. план является вырожденным, то не будет хватать количества уравнений для определения потенциалов. В этом случае целесообразно поменять местами поставщиков и потребителей или ввести в свободную ячейку с наименьшим тарифом нулевую (фиктивную) поставку.

Фиктивная перевозка может появиться также при перераспределении поставок, если окажется, что существует несколько наименьших объемов перевозок, стоящих в «минусовых» ячейках цикла. Тогда любую одну ячейку считаем свободной, а остальные - занятыми фиктивными объемами перевозок.

Шаг 4. Определение значения целевой функции путем суммирования произведений тарифов на объем перевозимого груза по всем занятым ячейкам распределительной таблицы.

Шаг 5. Проверка опорного плана на оптимальность:

1) расчет потенциалов. Для каждой занятой объемами перевозок клетки распределительной таблицы записываем уравнение

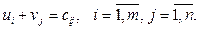(3.4)

Получим систему уравнений относительно чисел u_i и v_j, называемых потенциалами. Эта система имеет m + n -1 уравнений с m + n переменными. Так как число уравнений меньше числа переменных, то система является неопределенной и имеет бесконечное число решений. Поэтому полагаем u₁ = 0;

2) расчет оценок свободных ячеек. Для ячеек, не занятых объемами перевозок (свободные ячейки), считаем оценки:

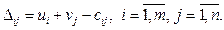(3.5)

Если все D_ij < 0, то опорный план является оптимальным. Если хотя бы одна оценка свободной ячейки положительна, то план не является оптимальным. Тогда необходимо осуществить перераспределение поставок груза, чтобы построить новый опорный план.

Шаг 6. Перераспределение груза.

Из ячейки, которой соответствует наибольшая положительная оценка, начинаем строить цикл, поставив в этой ячейке знак «+». Цикл - это замкнутая ломаная линия, звенья которой параллельны строкам и столбцам таблицы, а вершины лежат в занятых ячейках. Вершинам цикла поочередно присваиваем знаки «+» и «-». Из объемов груза, стоящих в «минусовых» ячейках, выбирают наименьший и обозначают d. В новой таблице прибавляют d к объемам груза в «плюсовых» ячейках и вычитают d из объемов «минусовых» ячеек.

Шаг 7. Получение нового опорного плана. Описанная процедура повторяется несколько раз (итераций), пока не будет найдено оптимальное решение. Если в оптимальном плане среди оценок свободных ячеек нет нулевых оценок, то найденный оптимальный план является единственным. Если же среди оценок свободных ячеек есть нулевая оценка, то задача имеет множество оптимальных планов (множество решений). Для ячейки с нулевой оценкой можно построить цикл и перераспределить груз. В результате полученный оптимальный план будет иметь то же значение целевой функции.

Пример 1. По данным о запасах груза на трех складах, потребностях в грузе у четырех магазинов и тарифах на перевозки, приведенных в таблице 3.2, определить оптимальный план перевозок груза с наименьшей стоимостью.

Таблица 3.2

Bj	В1	В2	В3	В4
Ai
А1
А2
А3

Решение. Обозначим через х_ij количество груза, перевозимого из пункта i в пункт j, где .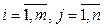

Балансовое равенство выполняется (суммарная потребность в грузе равняется суммарным запасам: 7 + 8 + 6 = 3 + 6 + 7 + 5), значит, транспортная задача - закрытая. Тогда экономико-математическая модель задачи выглядит следующим образом:

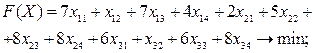
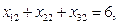
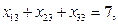
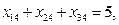
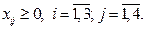
Вариант 1. Построим исходный опорный план методом северо-западного угла. В левую верхнюю ячейку делаем максимально возможную поставку х₁₁ =min(a₁; b₁) = min(7; 3) = 3. Тем самым на первом складе остается 4 ед. груза, а потребности первого магазина удовлетворены полностью, поэтому следующую перевозку будем осуществлять с первого склада ко второму потребителю: x₁₂ = min(a₁- 3; b₂) = min(4; 6) = 4. Так как при этом на первом складе запас груза исчерпан, а потребности второго магазина удовлетворены не полностью, то производим поставку со второго склада второму магазину: х₂₂ = min(a₂; b₂- 4) = min(8; 2) = 2. Продолжаем до тех пор, пока все запасы не будут исчерпаны, а потребности магазинов не удовлетворены полностью. В итоге получаем (табл. 3.3).

Таблица 3.3

bj аi
			-	-
	-			-
	-	-

или

.

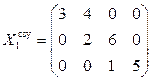Проверим найденный опорный план на вырожденность. Вычислим m + n -1= 3+4-1 = 6; число занятых ячеек равно 6. Так как эти значения совпадают, то найденный опорный план является невырожденным. Посчитаем стоимость перевозки:

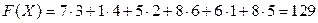ден. ед.

Вариант 2. Построим исходный опорный план методом наименьшего тарифа. На первом шаге заполняется ячейка с наименьшим тарифом 1. Заметим, что таких ячеек две, но, так как максимальные объемы поставок в обе ячейки одинаковы, заполнение таблицы можно начать как с той, так и с другой ячейки. Будем осуществлять поставку с первого склада ко второму потребителю: х₁₂ =min(a₁; b₂)=min(7;6) =6. Тем самым на первом складе осталась 1 ед. груза, а потребности второго магазина удовлетворены полностью. Поэтому далее выбираем ячейку с наименьшим тарифом из первого, третьего и четвертого столбцов таблицы. Будем осуществлять поставку со второго склада к первому потребителю: х₂₁ = min(a₂; b₁) = min(8;3)=3. Далее заполнение таблицы происходит следующим образом:

х₁₃ = min(a₁- 6; b₃) = min(1;5) = 1;

х₃₃ = min(a₃; b₃) = min(6;7) = 6;

х₂₃ =min(a₂- 3; b₃- 6)=min(5;1)=1;

х₂₄ =min(a₂- 3-1; b₄- 1)=min(4;4)=4.

Исходный опорный план, построенный методом наименьшего тарифа, следующий (табл. 3.4).

Таблица 3.4

bj аi
	-		-
		-
	-	-		-

или

.

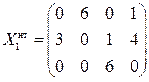Проверим найденный опорный план на вырожденность. Вычислим m + n -1=6; число занятых ячеек равно 6. Так как эти значения совпадают, то найденный опорный план является невырожденным.

Стоимость перевозки:

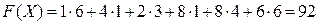ден. ед.

Практически всегда метод наименьшего тарифа дает более приближенный к оптимальному опорный план, чем метод северо-западного угла. Проверим план, построенный методом наименьшего тарифа, на оптимальность. Для этого по занятым объемами перевозок ячейкам составим систему уравнений по формуле (3.4):

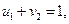
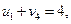
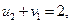
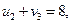
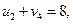
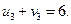
Неизвестные потенциалы u₁, u₂, u₃, v₁, v₂, v₃, v₄ находим из этой системы уравнений, полагая u₁ =0. Тогда из первого и второго уравнений: v₂ =1, v₄ =4; далее из предпоследнего: u₂ =4; затем из третьего и четвертого уравнений: v₁ =-2, v₃ =4; наконец, из последнегоуравнения: u₃ =2. Перепишем матрицу перевозок, добавив справа столбец с потенциалами u_i, а внизу - строку с потенциалами v_j (табл. 3.5).

Таблица 3.5

bj аi					ui
	-		-
		-
	-	-		-
vj	-2

Посчитаем оценки свободных ячеек по формуле (3.6):

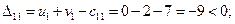
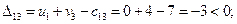
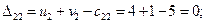
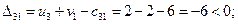
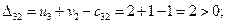
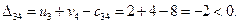
План не оптимальный, так как оценка D₃₂ положительна, поэтому ставим в этой ячейке знак «+» и строим цикл (табл. 3.6). Заметим, что такой цикл всегда существует и он единственный.

Таблица 3.6

bj аi					ui
	-	1 6	-	4 1
		-	8 1	8
	-	1 -	6	-
vj	-2

Наименьший объем груза в «минусовых» ячейках: d = 4. Новую таблицу перевозок составляем с учетом следующих изменений: в ячейках со знаком «+» объем перевозок увеличится на 4 ед., в ячейках со знаком «-» уменьшится на 4 ед., а в остальных останется без изменений (табл. 3.7).

Таблица 3.7

bj аi					ui
	-		-
		-		-
	-			-
vj

или

.

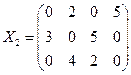Для проверки полученного плана на оптимальность по формуле (3.4) составляем систему уравнений:

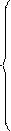
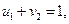
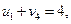
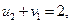
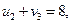
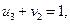
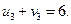
Решив систему, получаем новые значения для потенциалов u_i, v_j, которые заносим в таблицу перевозок (таблица 3.7).

По формуле (3.5) определим оценки свободных ячеек:

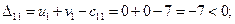
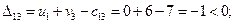
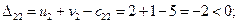
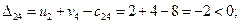
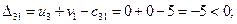
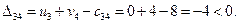
Проверяя план на оптимальность, замечаем, что все оценки свободных ячеек не положительны, т.е. полученный план перевозок является оптимальным. Стоимость перевозки: min F (X^*) = 84 ден. ед.

Открытая транспортная задача

В открытой транспортной задаче сумма запасов не совпадает с суммой потребностей, т.е.

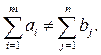
1. Если 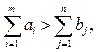то объем запасов превышает объем потребления, все потребители будут удовлетворены полностью и часть запасов останется невывезенной. Для решения задачи вводят фиктивного (n +1)-го потребителя, потребности которого

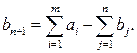
Модель такой задачи будет иметь вид

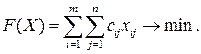
2. Если 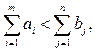то объем потребления превышает объем запасов, часть потребностей останется неудовлетворенной. Для решения задачи вводим фиктивного (m +1)-го поставщика:

Модель такой задачи будет иметь вид

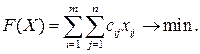
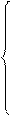
После введения фиктивного поставщика (потребителя) открытая транспортная задача становится закрытой и решается по рассмотренному алгоритму для закрытых транспортных задач, причем тариф, соответствующий фиктивному поставщику (потребителю), принимается больше или равным максимальному из всех транспортных тарифов, иногда его считают равным нулю. В значении целевой функции фиктивный поставщик (потребитель) не учитывается.

Пример 2. Составить оптимальный план перевозки грузов от трех поставщиков с грузами 240, 40, 110 т к четырем потребителям с запросами 90, 190, 40 и 130 т. Стоимость перевозок единицы груза от каждого поставщика к каждому потребителю с_ij задана матрицей

.

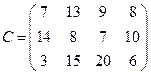Решение. Равенство (3.3) не выполняется, поэтому задача открытая, так как суммарная потребность в грузе превышает суммарный запас на 60 т. Для решения этой задачи вводим фиктивного поставщика с запасом груза 60 т.

Модель задачи запишется следующим образом: х_ij - количество груза, перевозимого из пункта i в пункт j, где .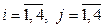

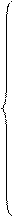
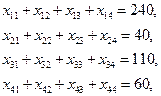
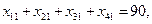
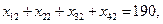
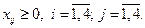
Построение исходного опорного плана, проверка плана на оптимальность и переход в случае неоптимального плана к новому для открытой транспортной задачи осуществляются точно так же, как и для закрытой.

Исходное опорное решение, найденное методом наименьшего тарифа, следующее (табл. 3.8).

Таблица 3.8

bj аi
	-		-
	-	0		-
		-	-
	-		-	-

или

.

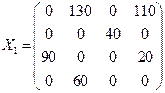Проверим исходный опорный план на вырожденность. Вычислим m + n -1= 4+4-1 = 7; число занятых ячеек равно 6. Так как эти значения не совпадают, найденный опорный план является вырожденным. Для исключения вырожденности поместим нулевую поставку в ячейку (2,2).

Оценки свободных ячеек равны:

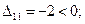
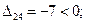
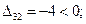
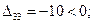
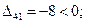
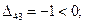
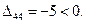
План не оптимальный, так как оценка D₁₃ больше нуля, перераспределим грузы (табл. 3.9).

Таблица 3.9

bj аi					ui
	-	13 130	9 -
	-	8 0	7	-	- 5
		-	-		- 2
	-		-	-
vj

Запишем полученное перераспределение грузов в таблицу 3.10.

Оценки свободных ячеек: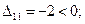

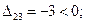
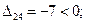
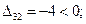
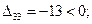
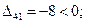
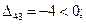
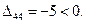
Таблица 3.10

bj аi					ui
	-
	-	40	-	-	- 5
		-	-		- 2
	-		-	-
vj

или

.

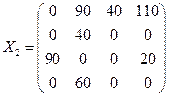Так как все оценки свободных ячеек положительные, получили оптимальное решение. Чтобы получить оптимальный план исходной задачи, нужно отбросить последнюю строку, соответствующую фиктивному поставщику:

.

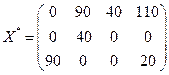Отброшенная строка плана Х^* означает, сколько единиц груза недополучат потребители, а именно второй потребитель недополучит 60 т груза.

Решение транспортных задач с использованием MSExcel

Решим задачу примера 1 в MS Excel.

Экранная форма, задание переменных, целевой функции и ограничений задачи и ее решение представлены на рис. 3.1-3.3 и в таблице 3.11.

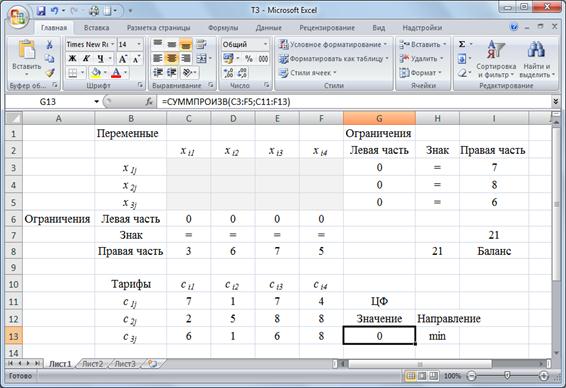
Рисунок 3.1 – Экранная форма

Таблица 3.11

Объект математической модели	Выражение в MS Excel
Переменные задачи	C3:F5
Формула в целевой ячейке G13	=CУMMПРOИЗB(C3:F5;C11:F13)
Ограничения по строкам в ячейках G3, G4, G5	=CУMM(C3:F3) =CУMM(C4:F4) =CУMM(C5:F5)
Ограничения по столбцам в ячейках С6, D6, Е6, F6	=СУММ(С3:С5) =CУMM(D3:D5) =СУММ(Е3:Е5) =CУMM(F3:F5)
Суммарные запасы и суммарные потребности в ячейках I7, Н8	=СУММ(I3:I5) =CУMM(C8:F8)

Ограничения неотрицательности переменных () можно задать в виде ограничения $C$3:$F$5>=0 или установить флажок «Неотрицательные значения» в окне «Параметры поиска решения».

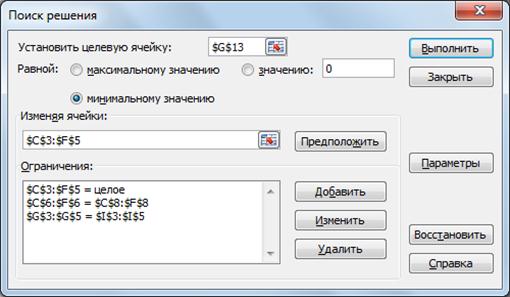
Рисунок 3.2 – Ограничения

Требование целочисленности ($C$3:$F$5=целое) задается, если это требуется по условию задачи.

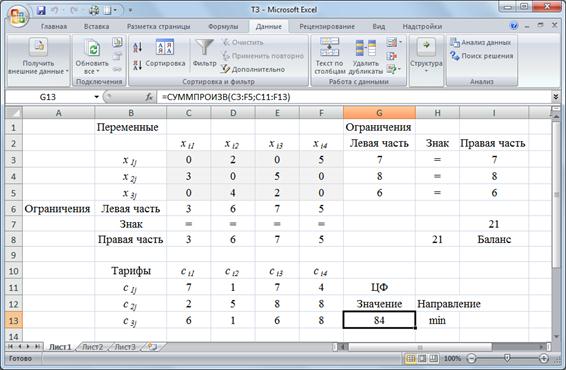
Рисунок 3.3 – Экранная форма после получения решения

Дата добавления: 2014-10-22