II. Дисперсия дискретной случайной величины

Опр.: Дисперсия случайной величины (дискретной или непрерывной) – это математическое ожидание квадрата ее отклонения от математического ожидания :

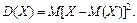
Замечание 1: Для дискретной случайной величины из определения математического ожидания следует формула для вычисления дисперсии:

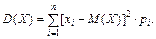
Замечание 2: «Дисперсия» в переводе означает «рассеяние» и является характеристикой разброса значений дискретной случайной величины вокруг среднего.

Задача 5.8: Найти дисперсию для дискретных случайных величин и 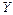из условия задачи 5.5.

Решение:

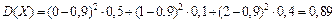
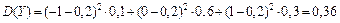
Свойства дисперсии:

1.

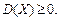
2.

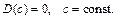
3.

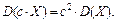
4.

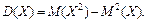
5.

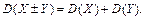
Замечание: Свойство 4 более удобно для вычисления дисперсии, чем определение.

Задача 5.9: 1) найти дисперсию дискретной случайной величины 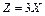из задачи 5.5; 2) найти дисперсии дискретных случайных величин 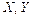из задачи 5.5 с помощью 4 свойства дисперсии; 3) найти дисперсию для величины 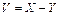из задачи 5.5.

Решение:

1)

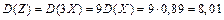
2)

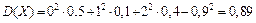
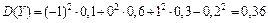
3)

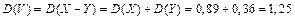
III. Среднее квадратическое отклонение дискретной случайной величины

Опр.: Среднее квадратическое отклонение дискретной случайной величины – это арифметическое значение квадратного корня из ее дисперсии:

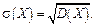
Замечание: Среднее квадратическое отклонение, как и дисперсия, характеризует разброс значений случайной величины вокруг ее математического ожидания, но имеет ту же размерность, что и случайная величина, в отличие от дисперсии.

Задача 5.10: Найт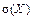и и 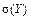для СВ 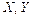из задачи 5.5.

Решение:

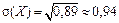
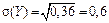
IV. Мода дискретной случайной величины

Опр.: Мода дискретной случайной величины – это ее наиболее вероятное значение, которое обозначается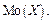

Замечание: Некоторые случайные величины полимодальны (то есть имеют несколько значений моды).

Свойства моды:

1. 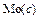не существует,

2.

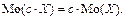
3. В общем случае

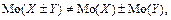
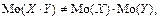
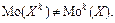
Задача 5.11: Найти моды дискретных случайных величин 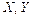из примера 5.5.

Решение:

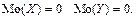
6.1. Моменты случайных величин

Опр.: Начальным моментом порядка дискретной или непрерывной случайной величины называется математическое ожидание этой случайной величины, возведенной в степень :

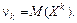
Замечание 1: Из определений математического ожидания и степени дискретной случайной величины следует, что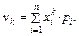

Замечание 2: Первый начальный момент случайной величины есть ее математическое ожидание: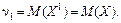

Задача 6.1: Найти начальные моменты 1–4 порядков для дискретной случайной величины из задачи 5.5.

Решение: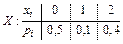

Опр.: Центральным моментом порядка 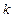дискретной или непрерывной случайной величины называется математическое ожидание возведенного в степень отклонения случайной величины от ее математического ожидания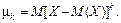

Замечание 1: Из определения математического ожидания и операций над дискретными случайными величинами следует формула:

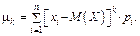
Замечание 2:

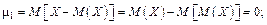
Замечание 3: Центральные моменты случайной величины можно выразить через начальные:

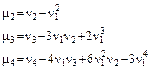
Задача 6.2: Найти центральные моменты для дискретной случайной величины из задачи 5.5.

Решение:

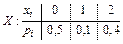
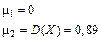
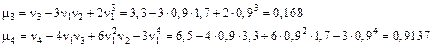
Опр.: Коэффициентом асимметрии дискретной или непрерывной случайной величины называется число, вычисляемое по формуле:

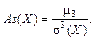
Коэффициент асимметрии характеризует асимметрию (скошенность) распределения случайной величины:

– если 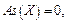то распределение симметрично относительно математического ожидания;

– если 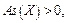то асимметрия правосторонняя (то есть случайная величина чаще принимает значения, которые больше );

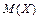– если 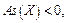то асимметрия левосторонняя (то есть случайная величина чаще принимает значения, меньшие ).

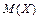Задача 6.3: Найти коэффициент асимметрии для дискретной случайной величины из задачи 5.5.

Решение: 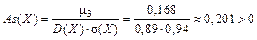– асимметрия правосторонняя.

Ответ: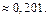

Опр.: Коэффициентом эксцесса дискретной или непрерывной случайной величины называется число, вычисляемое по формуле:

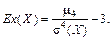
Коэффициент эксцесса характеризует крутость (остро- или туповершинность) распределения случайной величины по сравнению с нормальным:

– – крутость распределения такая же, как и у нормального;

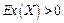– – вершина графической формы закона распределения более острая, чем у нормального;

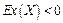– – вершина графической формы закона распределения тупее, чем у нормального.

Задача 6.4: Найти коэффициент эксцесса для дискретной случайной величины из задачи 5.5.

Решение: 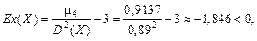поэтому вершина многоугольника распределения более тупая, чем у нормального.

Ответ: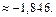

6.2. Непрерывная случайная величина

и её функция распределения

Опр.: Случайная величина называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

Замечание: Возможные значения непрерывной случайной величины нельзя пересчитать, поэтому для нее нельзя построить ряд распределения. Кроме того, табличная форма закона распределения не годится для непрерывной случайной величины, так как верна следующая теорема.

Теорема 6.1: Вероятность того, что непрерывная случайная величина в результате опыта примет конкретное изолированное значение, равна нулю: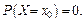

Следствие: Вероятность того, что значение непрерывной случайной величины в результате опыта попадет в промежуток, не зависит от того, открытый он или закрытый:

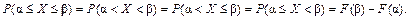
6.3. Плотность вероятности

непрерывной случайной величины

Опр.: Производная от функции распределения 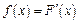непрерывной случайной величины называется плотностью распределения вероятностей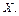

Замечание: Функция 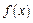является еще одной аналитической формой закона распределения непрерывной случайной величины. Ее график, в свою очередь, представляет собой еще одну графическую форму закона и называется кривой распределения.

Задача 6.5: Непрерывная случайная величина задана функцией распределения:

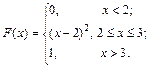
Найти плотность вероятности. Построить графики обеих функций.

Решение: Плотность вероятности найдем по определению:

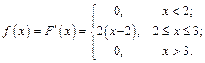
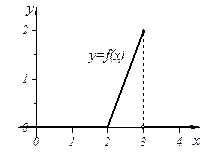
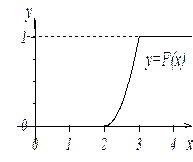
Свойства плотности вероятности:

1.

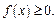
2. Вероятность попадания значений непрерывной случайной величины в промежуток от 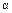до 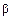равна определенному интегралу от

ее плотности вероятности на отрезке

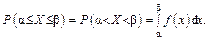
Задача 6.6: Найти вероятность попадания значений непрерывной случайной величины из задачи 6.5 в интервал (2,5; 2,75).

Решение: Искомую вероятность можно получить двумя способами: с помощью свойства 2 плотности вероятности:

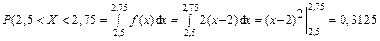
или формулы – следствия из теоремы 6.1.

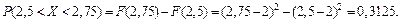
Ответ: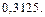

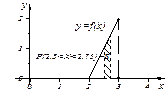Замечание: Для НСВ вероятность 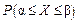принять значение на отрезке численно равна площади криволинейной трапеции, которая ограничена кривой распределения, осью 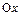и прямыми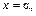

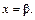
3. По заданной плотности вероятности непрерывной случайной величины можно найти ее функцию распределения:

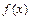Замечание: В случае если некоторая интегрируемая на отрезке функция задана на части этого отрезка аналитическим выражением 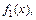а на другой части 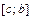отрезка аналитическим выражением 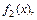то интеграл 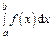нужно представить в виде суммы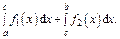

Задача 6.7: Для непрерывной случайной величины восстановить функцию распределения по заданной плотности вероятности:

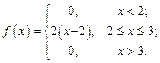
Решение: Используем для восстановления функции 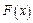формулу 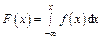на каждом промежутке, где функция 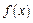задана различными аналитическими выражениями.

1. Если 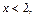то на 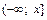по условию 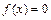и 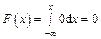на этом промежутке. Таким образом, при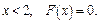

2. Если 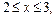то промежуток 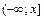надо разбить на части, поскольку 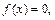на а на 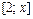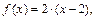и у каждой из функций своя первообразная, тогда для любого значения аргумента .

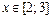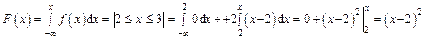
Таким образом, при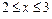

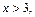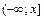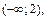
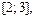
3. Если то промежуток придется разбить на три части: так как на каждой из частей плотность вероятности 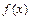задается разными аналитическими выражениями, и имеет, соответственно, различные первообразные:

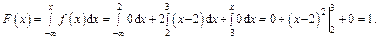
Таким образом, при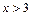

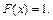
Обобщим результаты в виде формулы:

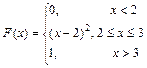
Она совпадает с исходной формулой из задачи 6.5, с помощью которой была найдена плотность вероятности.

Замечание: В геометрическом смысле в любой точке 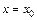значение функции 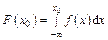равно площади фигуры, ограниченной кривой распределения 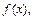осью 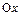и прямой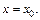

4.

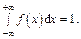
Замечание: Геометрически свойства 1 и 4 означают, что площадь криволинейной трапеции, ограниченной кривой распределения и осью 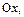равна единице.

Задача 6.8: Доказать, что функция 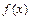из задачи 6.5 является плотностью вероятности для некоторой непрерывной случайной величины.

Решение: данная функция будет плотностью вероятности некоторой случайной величины, если для нее будут выполняться свойства 1 и 4. Проверим их выполнение.

Очевидно, что 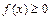на любом из промежутков 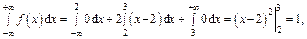поэтому заданная функция обладает свойствами плотности вероятности.

Дата добавления: 2014-10-23