Задачи линейного программирования

К задачам линейного про­граммирования относится поиск оптимума целевой линейной функции при наличии ограничений в виде линейных уравнений и неравенств. Некоторые задачи после ряда допущений могут быть приведены к форме, допускающей их решение этими методами.

В общем виде формулировка задачи сводится к следующему. Найти оптимум (максимум или минимум) целевой функции

F = c ₁ x ₁ + c ₂ x ₂ +…+ c _n x _n (Г.1)

при выполнении ограничений:

a ₁₁ x ₁ + a ₁₂ x ₂ +…+ a _1n x _n = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ +…+ a _2n x _n = b ₂

............ (Г.2)

a _m1 x ₁ + a _m2 x ₂ +…+ a _mn x _n = b _m ,

где коэффициенты a_ij, b_i, c_j – заданные постоянные величины, а число уравнений m меньше числа переменных n. Значение X = (x ₁, х ₂, …, x _n), при котором функция F имеет оптимум, называется оптимальным решением.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, например вида

a ₁₁ x ₁ + a ₁₂ x ₂ +…+ a _1n x _n£ b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ +…+ a _2n x _n£ b ₂

............ (Г.3)

a _m1 x ₁ + a _m2 x ₂ +…+ a _mn x _n£ b _m.

Однако любую систему ограничений можно привести к системе уравнений вида (Г.2). Для этого достаточно к левой части каждого неравенства добавить какое-то неотрицательное число x _n+1, x _n+2, x _n+m - добавочную переменную, чтобы неравенства обратились в уравнения. В результате вместо системы неравенств (Г.3) получим эквивалентную систему уравнений вида

a ₁₁ x ₁ + a ₁₂ x ₂ +…+ a _1n x _n+ x _n+1 = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ +…+ a _2n x _n+ x _n+2 = b ₂

............ (Г.4)

a _m1 x ₁ + a _m2 x ₂ +…+ a _mn x _n+ x _n+m = b _m,

т. е. систему ограничений, аналогичную системе (Г.2).

Таким образом, как бы ни были первоначально заданы огра­ничения задачи линейного программирования, их всегда можно привести к системе линейных уравнений, используя для этой цели добавочные переменные. Число добавочных переменных меньше m и равно m-t, где t – число ограничений в виде уравнений. Отсюда следует, что формулировка задачи (Г.1) - (Г.2) является формулировкой общей задачи линейного программирования. Ниже приведены примеры двух типовых задач линейного программирования.

Задача об оптимальном использовании ресурсов. Предприятие выпускает n различных изделий, и для их производства требуется m различных видов ресурсов (сырья, вспомогательных материалов, рабочего времени и т. д.). Эти ресурсы ограничены и составляют в планируемый период соответственно b ₁, b ₂,..., b _m условных единиц. Известны также технологические коэффициенты а_ij, которые указывают, сколько единиц i -го ресурса требуется для производства единицы изделия j -гo вида (i = 1, 2,..., m; j = 1, 2, …, n). Пусть прибыль, получаемая предприятием при реализации единицы изделия j -гo вида, равна c_j. Требуется составить такой план выпуска продукции x ₁, х ₂, …, x _n, чтобы на ее производство хватило имеющихся в распоряжении ресурсов и при реализации которого прибыль F = c ₁ x ₁ + c ₂ x ₂ +…+ c _n x _n была бы наибольшей. Математически эта задача сводится к поиску максимума функции F при ограничениях (Г.3).

Задача о смесях. Свойства смеси обеспечиваются наличием m различных компонентов в количествах не ниже заданных b ₁, b ₂,..., b _m, а сами компоненты являются составными частями n исходных материалов. Коэффициенты а_ij показывают удельный вес i -гo компонента (i = 1,…, m) в единице j -гo материала (j = 1,…, n). Необходимо отыскать наиболее дешевый набор x ₁, х ₂, …, x _n из n исходных материалов c ценой единицы j -гo материала с _j, обеспечивающий получение смеси. Задача сводится к отысканию минимума функции F = c ₁ x ₁ + c ₂ x ₂ +…+ c_nx _nпри ограничениях, аналогичных (Г.3), но со знаком «³».

Методы решения задач линейного программирования основываются на ряде положений (теорем), суть которых может быть сведена к следующему: оптимальное решение задачи линейного программирования совпадает с одной из угловых точек выпуклого множества решений для системы ограничений задачи. Общепризнанным универсальным методом решения задач линейного программирования в настоящее время является симплексный метод Данцига, алгоритм которого имеется в программном пакете MATLAB [24].

Если система ограничений задачи линейного программирования задана в виде системы линейных неравенств с двумя переменными или в виде системы линейных уравнений, в которой число переменных на два превышает число уравнений, то такие задачи могут быть решены геометрически. Геометрический метод представляет определенный интерес для выработки наглядных представлений о задачах линейного программирования.

Сущность этого метода заключается в построении области ограничений задачи на плоскости и поиске оптимального решения среди угловых точек этой области. Например, требуется найти максимум F = 4 x ₁ + 3 x ₂ при ограничениях x ₁ + 2 x ₂ £ 16 2 x ₁ + 3 x ₂ £ 28 3 x ₁ + 3 x ₂ £ 30 x ₁£ x ₂ x ₁³ 0; x ₂³ 0  

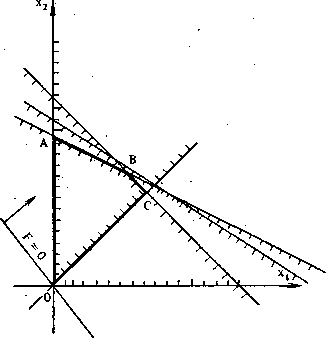
На рисунке изображена область решений системы ограничений в виде многоугольника ОАВС. Он образован прямыми линиями, соответствующими неравенствам системы ограничений, каждое из которых определяет отмеченную штриховкой полуплоскость допустимых значений переменных x ₁и x ₂. Отметим, что второе неравенство системы оказалось лишним, и соответствующая прямая 2 х ₁ + 3 х ₂ = 28 не участвовала в образовании четырехугольника ОАВС. Исходная линия уровня F = 4 x ₁ + 3 x ₂ = 0 показана прямой, проходящей через начало координат и точку (-3; 4).

Двигая исходную линию уровня в направлении стрелки, можно достигнуть максимума F,расположенного в точке С. Решив совместно уравнения для 3-й и 4-й прямых системы, получим координаты точки их пересечения С (x ₁ = 5; x ₂ = 5). Это оптимальное решение дает F_max = 35.

Библиографический список

1. Абдулин С.Ф. Автоматизация химических производств. – Омск: Изд-во ОмГТУ, 2002. –144 с.

2. Шувалов В.В., Огаджанов Г.А., Голубятников В.А. Автоматизация производственных процессов в химической промышленности. – М.: Химия, 1991. – 480 с.

3. Голубятников В.А., Шувалов В.В. Автоматизация производственных процессов в химической промышленности. – М.: Химия, 1985. – 350 с.

4. Автоматическое управление в химической промышленности: Учеб­ник для вузов / Под ред. Е.Г. Дудникова. – М.: Химия, 1987. – 368 с.

5. Кафаров В.В., Макаров В.В. Гибкие автоматизированные производст­венные системы в химической промышленности: Учебник для вузов. – М.: Химия, 1990. – 320 с.

6. Кафаров В.В., Мешалкин В.П. Анализ и синтез химико-технологи­ческих систем: Учебник для вузов. – М.: Химия, 1991. – 432 с.

7. Клюев А.С., Лебедев А.Т., Миф Н.П. Метрологическое обеспечение АСУТП. – М.: Энергоатомиздат. 1995. – 160 с.

8. Копысицкий Т.И. и др. Системы управления установками первичной переработки нефти. – М.: ЦНИИТЭнефтехим, 1997. – 47 с.

9. Степанов С.А. Теория систем автоматического управления (Цифровые системы управления): Учеб. пособие / Под ред. М.Н. Каткова. – СПб.: ГГЭТУ, 1994. – 159 с.

10. Полоцкий Л.М., Лапшенков Г.И. Автоматизация химических производств. Теория, расчет и проектирование систем автоматизации. – М.: Химия, 1982. – 296 с.

11. Техника чтения схем автоматического управления и технологическо­го контроля. 3-е изд., перераб. и доп. /А.С.Клюев, Б.В. Глазов, М.Б. Миндин, С.А. Клюев; Под ред. А.С. Клюева. М.: Энергоатомиздат. 1991. 432 с.

12. Технические средства автоматизации химических производств: Спра­вочное издание / B.C. Балакирев, Л.А. Барский, А.В. Багров и др. – М.: Химия, 1991. – 272 с.

13. Приборы для измерения и регулирования температуры: Каталог 1.1. Приборы и средства автоматизации. – М.: Информприбор. Ч. I-II. 2001.

14. Приборы для измерения и регулирования уровня жидкостей и сыпу­чих сред. Ката-лог 1.4. Приборы и средства автоматизации. – М.: Информ­прибор. 2001.

15. Приборы для нефтяной и газовой промышленности: Каталог 4. При­боры и средства автоматизации. – М.: Информприбор. 2001.

16. Вторичные приборы: Каталог 1.6. "Приборы и средства автоматиза­ции". – М.: Информприбор. 1998.

17. Датчики теплотехнических и механических величин: Справочник / А.Ю. Кузин, П.П. Мальцев, И.А. Шапортов, И.А. Беспалов. – М.: Энерго­атомиздат, 1996. – 128 с.

18. Багдадьев Е.Е. и др. Датчики теплофизических и механических па­раметров: Справочник / Общ. ред. Ю.Н. Коптев. – М.: Радиотехника. 1998. Т.1. Кн. 1-2. – 456 с.

19. Никонов А.В. Измерительные приборы со средствами вычислитель­ной техники: Учеб. пособие. – Омск: Изд-во ОмГТУ, 1996. – 123 с.

20. Ситников Д.В. Теория автоматического управления: Учеб. пособие. – Омск: Изд-во ОмГТУ, 2003. – 40 с.

21. Бернацкий Ф.И. и др. Автоматизированное управление процессами химической технологи­и. – М.: Наука, 1981. – 216 с.

22. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. - М.: Мир, 1985. - 509 с.

23. Автоматизированная система управления крупнотоннажным производством этилена / Под ред. Ю.М. Жорова. – М.: Химия, 1986. – 240 с.

24. Дьяконов В.П., Абраменкова И.В., Круглов В.В. MATLAB 5.3.1 с пакетами расширений. – М.: Нолидж, 2001.– 880 с.

25. Дьяконов В.П. MATLAB 6/ 6.1/ 6.5 + Simulink 4/5 в математике и моделировании. Полное руководство пользователя. – М.: СОЛОН-Пресс, 2003.– 576 с.

Редактор В.А. Маркалева

ИД № ________ от _______

Подписано к печати 25.10. 2004. Формат 60х84 ¹/₁₆. Бумага офсетная.

Отпечатано на дупликаторе. Усл. печ. л. 9. Уч.-изд. л. 9.

Тираж 100. Заказ

Издательство ОмГТУ. Омск, пр. Мира 11. Тел.: 23-02-12

Типография ОмГТУ

Дата добавления: 2014-10-23