И бароклинные течения

Для разных случаев движения. Баротропные

Интегралы уравнения движения жидкости

Если во всей области движения , то существует потенциал скорости , т.е.

(6.11)

или

. (6.12)

Тогда уравнение Эйлера в форме Громека примет вид

. (6.13)

Следовательно, выражение в скобках может зависеть только от времени, а от координат не зависит. Интеграл этого уравнения будет

, (6.14)

где определяется из граничных условий. Этот интеграл уравнения Эйлера называется интегралом Коши для потенциального движения идеальной несжимаемой жидкости.

Когда массовые силы являются только силами тяжести, потенциал этих сил принимает вид U = gz, а интеграл Коши

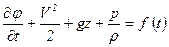. (6.15)

В уравнении (6.15) имеется два неизвестных и р, поэтому для решения задачи следует воспользоваться уравнением неразрывности

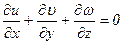. (6.16)

Подставляя в это уравнение значения проекций скорости, получим

. (6.17)

Уравнение (6.17) является уравнением Лапласа, решая которое можно найти . Подставив значение в уравнение (6.15) и имея в виду, что

, (6.18)

определим давление р. Произвольная функция будет найдена по величине р(t) в некоторой точке.

Если движение стационарно, т.е. , то уравнение (6.15) примет вид

. (6.19)

Этот интеграл уравнений Эйлера называется интегралом Бернулли для потенциального стационарного потока идеальной несжимаемой жидкости. Постоянная будет одной и той же для всей области потенциального потока.

Из уравнения Бернулли видно, что во всей области безвихревого потока энергия жидкости в единице массы остается постоянной. Первое слагаемое выражения (6.19) является кинетической энергией, второе - потенциальной и третье - работой сил давления.

Умножив все слагаемые уравнения (6.19) на величину плотности, получим интеграл Бернулли в виде суммы слагаемых, имеющих размерность давления

, (6.20)

где р - пьезометрический напор;

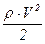- скоростной или динамический напор;

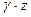- геометрический напор;

- полный напор.

В соответствии с уравнением (6.20) сумма динамического, пьезометрического и геометрического напоров во всей области потенциального потока остается величиной постоянной.

Разделив обе части уравнения (6.19) на g, получим уравнение Бернулли в виде

. (6.21)

Каждый член, входящий в уравнение (6.21), имеет размерность длины. Величину называют динамической высотой, - пьезометрической и z - геометрической высотой.

Согласно уравнению (6.21) сумма динамической, геометрической и пьезометрической высот во всей области потенциального потока остается величиной постоянной.

При отсутствии массовых сил интеграл Бернулли запишется в виде

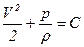(6.22)

или

. (6.23)

Если в уравнении (6.19) скорость V будем считать равной нулю, то получим интеграл уравнения Эйлера для гидростатики

. (6.24)

Для того чтобы проинтегрировать уравнения Эйлера (6.2) вдоль линии тока, проделаем некоторые преобразования. Умножим уравнения (6.2) соответственно на dx, dy, dz

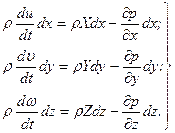. (6.25)

Затем, сложив почленно и разделив на , получим

. (6.26)

Отдельные слагаемые левой части уравнения, имея в виду стационарность потока, представим в виде

(6.27)

Уравнение (6.26) будет справедливо лишь на линии тока, если между элементами дуги и скоростью будут соблюдаться соотношения

(6.27)

или

. (6.28)

Используя последние равенства, получим

;

(6.29)

так как выражение в скобках представляет собой полный дифференциал. Окончательно левая часть уравнения (6.26) может быть представлена следующим образом

. (6.30)

Тогда, полагая наличие потенциала массовых сил, уравнение (6.26) запишем в виде

(6.31)

или

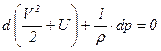. (6.32)

При постоянной плотности, что соответствует несжимаемой жидкости, получим

. (6.33)

Интегралом этого уравнения будет

(6.34)

или, имея в виду выражение потенциала сил тяжести, запишем

. (6.35)

Выражение (6.35) называется интегралом или уравнением Бернулли для линии тока.

Уравнение (6.35) тождественно с уравнением Бернулли для потенциального потока. Различие состоит в том, что при потенциальном потоке постоянная С сохраняет свое значение для всей области потока, а при вихревом потоке каждая линия тока имеет свое значение постоянной С. В случае вихревого движения постоянная С сохраняет свое значение и вдоль вихревой линии.

Когда плотность жидкости не постоянна, вид интеграла Бернулли определяется зависимостью плотности жидкости от параметров потока. Наиболее простым с точки зрения математики является движение, при котором плотность есть функция только от давления. Жидкости, плотность которых есть функция давления, называются баротропными. Для баротропных жидкостей плотность равна

. (6.36)

Тогда уравнение (6.32) для стационарного потока при наличии потенциала массовых сил будет

. (6.37)

Если ввести интеграл в виде

, (6.38)

то получим

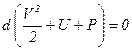(6.39)

или

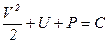. (6.40)

Последнее выражение есть интеграл Бернулли для баротропного движения.

Интеграл Бернулли для одномерного баротропного движения при отсутствии массовых сил имеет вид

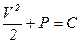, (6.41)

где Р - так называемая функция давления, значение которой определяется из выражения (6.36) при заданной связи между плотностью и давлением.

Для изотермического процесса функция давления равна

, (6.42)

следовательно, интеграл Бернулли будет иметь вид

. (6.43)

Жидкости, плотность которых есть функция не только давления, но и температуры, называют бароклинными. При течении бароклинных жидкостей их плотность определяется в виде

. (6.44)

Интеграл Бернулли является одним из основных уравнений гидравлики (механики жидкости и газа) и широко применяется в различных своих формах.

Дата добавления: 2014-10-31