
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон изменения количества движения
|
|
|
|
ЛЕКЦИЯ №7
Из курсов физики и теоретической механики известна теорема об изменении количеств движения, согласно которой производная по времени от главного вектора количеств движения 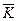 массы, заключенной в некотором объеме
массы, заключенной в некотором объеме 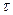 , равна главному вектору всех внешних сил
, равна главному вектору всех внешних сил 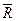 , приложенных к объему
, приложенных к объему
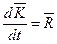 . (7.1)
. (7.1)
Рассмотрим применение этой теоремы к стационарно движущемуся потоку жидкости.
Когда количество движения жидкости в объеме 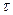 , заключенном внутри некоторой неподвижной (так называемой контрольной) поверхности s, будет равно
, заключенном внутри некоторой неподвижной (так называемой контрольной) поверхности s, будет равно
 . (7.2)
. (7.2)
Подставив значение  в уравнение (7.1), получим
в уравнение (7.1), получим
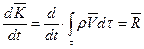 . (7.3)
. (7.3)
Так как, согласно закону о сохранении массы в течение всего времени масса частиц жидкости остается постоянной, т.е.  , то предыдущее равенство запишется следующим образом
, то предыдущее равенство запишется следующим образом
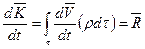 (7.4)
(7.4)
или в проекциях на оси координат
 ;
;
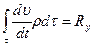 ; (7.5)
; (7.5)
 .
.
Сделаем далее преобразования лишь для проекции на ось х. Так как для стационарного движения  и
и
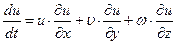 , (7.6)
, (7.6)
а
 ;
;
 ; (7.7)
; (7.7)
 .
.
то
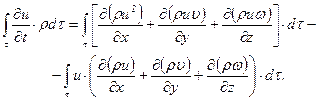 (7.8)
(7.8)
Очевидно, что второй интеграл в правой части обращается в нуль, так как при стационарном движении сжимаемой жидкости  .
.
Пользуясь формулой Остроградского - Гаусса для связи интегралов по поверхности s и по объему 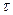 , заключенному в этой поверхности, в форме
, заключенному в этой поверхности, в форме
 , (7.9)
, (7.9)
получим выражение изменения количества движения в проекции на ось х в виде
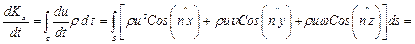

где
 (7.10)
(7.10)
есть проекция вектора скорости на нормаль к площадке ds и, следовательно, 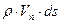 есть масса жидкости, проходящая через элементарную площадку контрольной поверхности s.
есть масса жидкости, проходящая через элементарную площадку контрольной поверхности s.
Проделав аналогичные операции с проекциями на оси у и z, получим
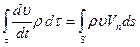 ; (7.11)
; (7.11)
 . (7.12)
. (7.12)
Следовательно, уравнение импульсов или закон изменения количеств движения для стационарного движения любых жидкостей и всех сплошных сред (мука, пыль, песок и пр.) можно представить в векторной форме в следующем виде
|
|
|
 . (7.13)
. (7.13)
Можно заметить, что полученный закон изменения количеств движения для сплошных сред существенно отличается от ранее приведенной его формулировки для твердого тела. Это отличие выражается в том, что вместо производной по времени от количества движения некоторого твердого тела с объемом 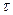 для сплошной среды рассматривается так называемый перенос количества движения через замкнутую контрольную поверхность s. Причем для определения изменения количеств движения некоторой массы жидкости, заключенной внутри контрольной поверхности, достаточно изучить только то, что происходит на этой контрольной поверхности.
для сплошной среды рассматривается так называемый перенос количества движения через замкнутую контрольную поверхность s. Причем для определения изменения количеств движения некоторой массы жидкости, заключенной внутри контрольной поверхности, достаточно изучить только то, что происходит на этой контрольной поверхности.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 486; Нарушение авторских прав?; Мы поможем в написании вашей работы!