Тема: чисельні методи розв’язування звичайних диференціальних рівнянь

Лабораторна робота 17.

Завдання.

Контрольні питання.

1. Що називають залишковим членом квадратурної формули?

2. Що означає число 10 у позначенні похибки квадратурної формули R₁₀(f)?

3. Чим вимірюють звичайно точність квадратурної формули?

4. Якщо з алишковий член квадратурної формули ôR(f)ô ≤ Сh^k для кроку інтегрування h, то чи означає це, що R(f) = О(h^k).

5. Чи завжди квадратурна формула тим точніша, чим більшим є порядок її залишкового члена?

6. Який порядок має залишковий член узагальненої квадратурної формули трапецій? Узагальненої квадратурної формули Сімпсона?

7. На яких формулах ґрунтується метод подвійного перерахунку? Випишіть їх.

8. На яке число треба поділити I_2n – I_n згідно з правилом Рунге, якщо порядок р = 5?

9. Який порядок має похибка, отримана методом подвійного перерахунку, якщо порядок методу р = 5?

10. Який порядок має похибка, отримана методом кратного перерахунку в результаті k перерахунків, якщо порядок методу р = 6?

Задача 1. Уточнити наближене значення інтеграла функції, отримане в лабораторній роботі 15 за узагальненою формулою трапецій, і оцінити його похибку методом кратного перерахунку.

Задача 2. Обчислити наближене значення функції f (x) з лабораторної роботи 15 за узагальненою формулою Сімпсона з точністю 10^-7, для оцінки похибки використавши метод кратного перерахунку.

Література:

1. Бахвалов Н.С. Численные методы – М: Наука, 1973. т. 1. – 631с.
2. Вейцбліт О.Й. Основи чисельних методів математики (з використанням Excel) – Херсон: Видавництво ХДУ, 2011. – 280 с.
3. Лященко М.Я., Головань М.С., Чисельні методи – К: Либідь, 1996 – 288с.

(2г.)

Мета: Отримати відомості про чисельні методи розв’язування звичайних

диференціальних рівнянь та навчитися застосовувати ці методи до

конкретних задач.

Теоретичні відомості.

Означення 1. 1. Звичайним диференціальним рівнянням називають таке рівняння, що зв’язує незалежну змінну х, невідому функцію у(х) і її похідні у´, у´´, …, у⁽ⁿ⁾.

2. Порядок рівняння – це порядок вищої похідної, що входить до нього.

3. Задача Коші для звичайного диференціального рівняння першого порядку

у´ = f (x, y); у(х₀) = у₀ (1)

полягає в тому, щоб знайти розв’язок у(х) цього рівняння, який задовольняє початкову умову у(х₀) = у₀.

Означення 2. 1. Розв’язати задачу Коші (1) чисельно означає для заданої послідовності х₀, х₁, …, х_n значень незалежної змінної х і числа у₀ знайти числову послідовність у₀, у₁, …, у_n так, щоб у_k з заданою точністю наближав у(х_k) для всіх k = 1, 2, …, n, де у(х) – єдиний розв’язок задачі Коші з початковою умовою у(х₀) = у₀.

2. Різницю у_k – у(х_k) називають похибкою наближеного значення у_k в точці х_k.

3. Якщо всі точки х₀, х₁, …, х_n рівновіддалені: х_k = х₀ + kh, то величину h називають кроком інтегрування диференціального рівняння.

Означення 3. Метод Ейлера є чисельний метод розв’язання звичайних диференціальних

рівнянь першого порядку, рекурентна формула якого має вигляд:

x_k+1 = x_k + h, у_k+1 = у_k + f (х_k; у_k)h (k = 0, 1, 2, …, n – 1). (2)

Метод Ейлера – це найстаріший та найпростіший метод чисельного інтегрування. Дещо модифікований алгоритм називають удосконаленим методом Ейлера.

Означення 4. Удосконалений метод Ейлера визначається рекурентною формулою

у_{k + ½} = у_k + 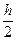f (х_k; у_k); у_k+1 = у_k + f (х_k + 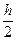; у_{k + ½})h (k = 0, 1, 2, …, n – 1). (3)

Виявляється, що похибка чисельного інтегрування на відрізку завдовжки одиниця для удосконаленого методу Ейлера є величиною порядку h² на відміну від h для методу Ейлера.

Хід роботи.

Задача 1) Знайти чисельні розв’язки задачі Коші у´(х) = 2у + 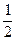sin(3x – y), y(0) = 1 на відрізку [0; 1] з кроками інтегрування h = 0,2 0,1 0,05 0,025 методомЕйлера.

2) Знайти удосконаленим методомЕйлера чисельні розв’язки тої ж задачі Коші з тими ж кроками інтегрування. Порівняти отримані результати.

Розв’язання. 1)Кроки інтегрування задамо у чарунках H1: H4 так, що H1 = 0,2, а H4 = 0,025. Побудуємо електронну таблицю для чисельного розв’язання даної задачі Коші з кроком інтегрування 0,2 методомЕйлера. Надамо чарункам таких значень:

	A	B	C
	x	y	Dy
			= $H$1*(2*B2+0,5*SIN(3*A2-B2))
	= A2+$H$1	= B2+C2	↓
	↓	↓	↓

Тут у чарунках А2:В2 координати початкової точки, у чарунці С2 підраховується кутовий коефіцієнт f (х₀; у₀), помножений на крок інтегрування, у стовпці А отримуються значення х_k з кроком 0,2 на відрізку [0; 1]. Тоді у стовпці В будуть обчислені відповідні значення у(х_k) згідно з рекурентною формулою (1). Символ ↓ означає копіювання попередніх чарунок. В результаті отримаємо таку таблицю:

	A	B	C
	х	у	Dy
			0,315853
	0,2	1,315853	0,460715
	0,4	1,776568	0,656112
	0,6	2,43268	0,913941
	0,8	3,346621	1,257504
		4,604125	1,741706

Звичайно, стовпець А копіюємо лише до чарунки із значенням 1, в даному випадку до А7. Звідси, наприклад, у(0,2) ≈ 1,315853, у(1) ≈ 4,604125. Для отримання аналогічної таблиці з кроком інтегрування 0,1 можна скопіювати попередні формули, наприклад, у діапазон Е1:G3, а потім у чарунках Е3 і G2 у $H$1 замінити 1 на 2. отримуємо таку таблицю:

	E	F	G
	x	y	Dy
			= $H$2*(2*F2+0,5*SIN(3*E2-F2))
	= E2+$H$2	= B2+C2	↓
	↓	↓	↓

І тоді в результаті обчислень дістанемо:

	E	F	G
	х	у	Dy
			0,157926
	0,1	1,157926	0,193761
	0,2	1,351687	0,236194
	0,3	1,587881	0,285831
	0,4	1,873712	0,343548
	0,5	2,21726	0,410586
	0,6	2,627846	0,488745
	0,7	3,116592	0,580802
	0,8	3,697394	0,691336
	0,9	4,38873	0,828093
		5,216823	1,003441

	J	K	L
	х	у	Dy
			0,039482
	0,025	1,039482	0,041702
	0,05	1,081184	0,04403
	0,075	1,125214	0,046467
	0,1	1,171681	0,049016
	0,125	1,220698	0,051679
	0,15	1,272377	0,054459
	0,175	1,326836	0,057359
	0,2	1,384195	0,060382
	0,85	4,432428	0,209723
	0,875	4,642152	0,220832
	0,9	4,862984	0,232778
	0,925	5,095762	0,245642
	0,95	5,341404	0,259503
	0,975	5,600907	0,274432
		5,875339	0,290478

Так само скопіюємо формули у два нових вільних діапазони, (скажімо у А9:С11 та J1:L3), і замінимо у відповідних чарунках в $H$1 1 відповідно на 3 і 4. В результаті (деякі рядки в наступних таблицях випущені) дістанемо:

	A	B	C
	х	у	Dy
			0,078963
	0,05	1,078963	0,087871
	0,1	1,166835	0,097626
	0,15	1,264461	0,108262
	0,2	1,372723	0,11982
	0,25	1,492543	0,13235

	0,55	2,513612	0,232356
	0,6	2,745968	0,25432
	0,65	3,000288	0,27834
	0,7	3,278628	0,304761
	0,75	3,583389	0,33404
	0,8	3,917429	0,366778
	0,85	4,284207	0,403754
	0,9	4,687961	0,44594
	0,95	5,133901	0,494482
		5,628383	0,550564

2) Тепер побудуємо електронну таблицю для чисельного розв’язання даної задачі Коші з кроком 0,2 удосконаленим методомЕйлера. Надамо чарункам таких значень:

	A	B	C
	x	y	Dy
			= $H$1*(2*B2+0,5*SIN(3*A2-B2))
	= A2 + $H$1	= B2 + F2	↓
	↓	↓	↓
	D	E	F
	x1	y1	Dy1
	= A2 + 0,5*$H$1	= B2 + 0,5*C2	= $H$1*(2*E2+0,5*SIN(3*D2-E2))
	↓	↓	↓
	↓	↓	↓

Формули у стовпцях А, В, С майже ідентичні відповідним формулам таблиці методу Ейлера, лише чарунці В3 надана формула = B2 + F2 замість = B2+C2 у методі Ейлера. Але в цьому й врахована відмінність цих методів: у стовпці В обраховуються значення згідно з (2) у_k+1 = у_k + f (х_k + 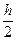; у_{k + ½})h, а доданок f (х_k + 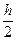; у_{k + ½})h підраховується в стовпці F. Його аргументи х_k + 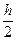і у_{k + ½} = у_k + 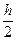f (х_k; у_k) обраховуються відповідно у стовпцях D і Е. Формулу у чарунці F2 можна просто скопіювати з чарунки С2. В результаті обрахунків за попередньою таблицею дістанемо:

	A	B	C	D	E	F
	x	y	Dy	x1	y1	Dy1
			0,315853	0,1	1,157926	0,387522
	0,2	1,387522	0,484148	0,3	1,629596	0,585181
	0,4	1,972703	0,719274	0,5	2,33234	0,858985
	0,6	2,831688	1,046859	0,7	3,355118	1,246989
	0,8	4,078677	1,532052	0,9	4,844703	1,853903
		5,93258	2,352282	1,1	7,108721	2,905362

Далі можна, як і в методі Ейлера, скопіювати попередні формули, наприклад у діапазон J1:O3, а потім у чарунках A3, C2, D2, F2 у $H$1 замінити 1 на 2, звідки дістанемо:

	J	K	L
	x	y	Dy
			= $H$2*(2*K2+0,5*SIN(3*J2-K2))
	= J2 + $H$2	= K2 + O2	↓
	↓	↓	↓
	M	N	O
	x1	y1	Dy1
	= J2 + 0,5*$H$2	= K2 + 0,5*L2	= $H$2*(2*N2+0,5*SIN(3*M2-N2))
	↓	↓	↓
	↓	↓	↓

І тоді (деякі проміжні рядки в наступній таблиці випущені) дістанемо:

	J	K	L	M	N	O
	x	y	Dy	x1	y1	Dy1
			0,157926	0,05	1,078963	0,175743
	0,1	1,175743	0,196748	0,15	1,274116	0,218126
	0,2	1,393869	0,24312	0,25	1,515429	0,268443
	0,3	1,662312	0,297933	0,35	1,811278	0,327763
	0,4	1,990075	0,362495	0,45	2,171323	0,397662
	0,8	4,152523	0,781328	0,85	4,543187	0,863032
	0,9	5,015555	0,966349	0,95	5,49873	1,076088
		6,091644	1,215832	1,05	6,69956	1,359749

Так само скопіюємо попередні формули у два нових вільних діапазони, а потім замінимо в $H$1 1 відповідно на 3 і 4 у відповідних чарунках. В результаті отримуємо таблиці:

	A	B	C	D	E	F
	x	y	Dy	x1	y1	Dy1
			0,078963	0,025	1,039482	0,083404
	0,05	1,083404	0,088249	0,075	1,127529	0,09313
	0,1	1,176535	0,09844	0,125	1,225755	0,103781
	0,15	1,280316	0,109578	0,175	1,335105	0,115401
	0,2	1,395717	0,121713	0,225	1,456574	0,128047
	0,9	5,048251	0,487008	0,925	5,291755	0,514551
	0,95	5,562803	0,545886	0,975	5,835746	0,577854
		6,140657	0,614042	1,025	6,447678	0,650494

та

	J	K	L	M	N	O
	x	y	Dy	x1	y1	Dy1
			0,039482	0,0125	1,019741	0,04059
	0,025	1,04059	0,04175	0,0375	1,061465	0,042913
	0,05	1,083503	0,044129	0,0625	1,105568	0,045348
	0,075	1,128851	0,046621	0,0875	1,152162	0,047897
	0,1	1,176749	0,049229	0,1125	1,201363	0,050564
	0,95	5,573824	0,27362	0,9625	5,710634	0,281618
	0,975	5,855442	0,290152	0,9875	6,000518	0,298734
		6,154175	0,307866	1,0125	6,308108	0,317014

Найбільшою є похибка у кінцевій точці 1. Порівняємо наближені значення розв’язку задачі Коші, отримані в задачі методом Ейлера та удосконаленим методомЕйлера у цій точці за допомогою наступної таблиці.

	Метод Ейлера	Удосконалений метод Ейлера
h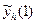
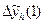
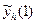
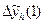
0,2	4,604125		5,93258
0,1	5,216823	0,612698	6,091644	0,159064
0,05	5,628383	0,41156	6,140657	0,049013
0,025	5,875339	0,246957	6,154175	0,013518

Тут у стовпці h використані в задачі кроки інтегрування диференціального рівняння; 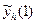– це наближене значення розв’язку задачі Коші в точці 1, отримане методом Ейлера або удосконаленим методомЕйлера з кроком h і взяте із відповідної попередньої таблиці. 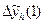– це 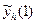– 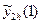, наприклад, для методу Ейлера 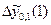= 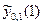–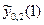= 5,216823 – 4,604125 = 0,612698. З таблиці відразу видно, що значення 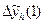для удосконаленого методуЕйлера відчутно менші відповідних значень методуЕйлера, тобто збіжність удосконаленого методуЕйлера значно швидша.

Дата добавления: 2014-10-31