Определение производной

Понятие производной

Пусть функция f (x) определена на некотором промежутке X. Придадим значению аргумента в точке x ₀ Х произволь­ное приращение Δ x так, чтобы точка x₀ + Δ x также принад­лежала X. Тогда соответствующее приращение функции f(x) составит Δ у = f (x₀ + Δ x) — f (x₀).

Определение 1. Производной функции f(x) в точке x₀ назы­вается предел отношения приращения функции в этой точке к приращению аргумента при Δ x 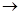0 (если этот предел сущест­вует).

Для обозначения производной функции употребимы симво­лы у' (x₀) или f '(x₀):

Если в некоторой точке x₀ предел (4.1) бесконечен:

то говорят, что в точке x₀ функция f (x) имеет бесконечную производную.

Если функция f (x) имеет производную в каждой точке мно­жества X, то производная f'(x) также является функцией от аргумента х, определенной на X.

Геометрический смысл производной

Для выяснения геометрического смысла производной нам понадобится определение касательной к графику функции в данной точке.

Определение 2. Касательной к графику функции у = f (x) в точке М называется предельное положение секущей MN, ког­да точка N стремится к точке М по кривой f (x).

Пусть точка М на кривой f (x) соответствует значению ар­гумента x₀, а точка N — значению аргумента x₀ + Δ x (рис. 4.1). Из определения касательной следует, что для ее существования в точке x₀ необходимо, чтобы существовал предел , который равен углу наклона касательной к оси Оx. Из треугольника MNA следует, что

Если производная функции f (x) в точке x₀ существует, то, согласно (4.1), получаем

Отсюда следует наглядный вывод о том, что производная f '(x₀) равна угловому коэффициенту (тангенсу угла наклона к положительному направлению оси Ох) касательной кграфику функции у = f (x) в точке М (x₀, f (x₀)). При этомуголнаклона касательной определяется из формулы (4.2):

Физический смысл производной

Предположим, что функция l = f (t) описывает закон дви­жения материальной точки по прямой как зависимость пути l от времени t. Тогда разность Δ l = f(t + Δ t) - f(t) — это путь, пройденный за интервал времени Δ t, а отношение Δ l /Δ t — средняя скорость за время Δ t. Тогда предел 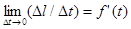определяет мгновенную скорость точки в момент вре­мени t как производную пути по времени.

В определенном смысле производную функции у = f(x) можно также трактовать как скорость изменения функции: чем больше величина f '(x), тем больше угол наклона касательной к кривой, тем круче график f (x) и быстрее растет функция.

Правая и левая производные

По аналогии с понятиями односторонних пределов функ­ции вводятся понятия правой и левой производных функции в точке.

Определение 3. Правой (левой) производной функции у = f(x) в точке x₀ называется правый (левый) предел отноше­ния (4.1) при Δ x 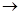0, если этот предел существует.

Для обозначения односторонних производных используется следующая символика:

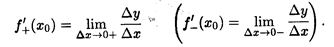
Если функция f (x) имеет в точке x₀ производную, то она имеет левую и правую производные в этой точке, которые сов­падают.

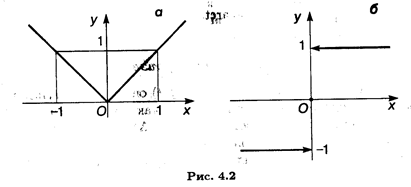
Приведем пример функции, у которой существуют одно­сторонние производные в точке, не равные друг другу. Это f (x) = | x |. Действительно, в точке х = 0 имеем f’₊ (0) = 1, f'_- (0) = -1 (рис. 4.2) и f’₊ (0) ≠ f’_- (0), т.е. функция не имеет производной при х = 0.

Операцию нахождения производной функции называют ее дифференцированием; функция, имеющая производную в точ­ке, называется дифференцируемой.

Связь между дифференцируемостью и непрерывностью функции в точке устанавливает следующая теорема.

ТЕОРЕМА 1. Если функция дифференцируема в точке x₀, то она и непрерывна в этой точке.

Обратное утверждение неверно: функция f (x), непрерыв­ная в точке, может не иметь производную в этой точке. Таким примером является функция у = | x |; она непрерывна в точке x = 0, но не имеет производной в этой точке.

Таким образом, требование дифференцируемости функции является более сильным, чем требование непрерывности, по­скольку из первого автоматически вытекает второе.

Уравнение касательной к графику функции в данной точке

Как было указано в разделе 3.9, уравнение прямой, про­ходящей через точку М (x₀, у₀) с угловым коэффициентом k имеет вид

Пусть задана функция у = f (x). Тогда посколькуее произ­водная в некоторой точке М (x₀, у₀) является угловым коэффи­циентом касательной к графику этой функции в точке М, то отсюда следует, что уравнение касательной к графику функ­ции f (x) в этой точке имеет вид

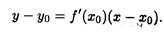
Дата добавления: 2014-10-15