Частотные критерии устойчивости

Среди частотных критериев устойчивости, используемых в практике анализа устойчивости непрерывных и дискретных систем автоматического управления, наибольшее признание получили критерий годографа характеристического полинома замкнутой системы (известный в отечественной литературе как критерий Михайлова) и критерий Найквиста, обеспечивающий определение устойчивости по виду частотных характеристик разомкнутой системы.

В основу названных выше критериев положено следствие из известного в теории функции комплексной переменной принципа аргумента. Оно устанавливает соответствие между числом корней в левой и правой полуплоскости и суммарным приращением аргумента вектора характеристического полинома замкнутой системы, при изменении частоты в диапазоне 0 £ w £ +¥. Рассмотрим это соответствие.

Характеристическое уравнение замкнутой непрерывной системы

D (s) = a ₀ sⁿ + a ₁ s^{n -1} + ¼ + a_n = 0,

где левая часть уравнения D(s) называется характеристическим полиномом. Его можно представить в соответствии с теоремой Безу следующим образом
D(s) = a₀(s – s₁) (s – s₂) ¼(s – s_i) ¼(s – s_n), где s_i (i =1, 2, ¼, n) – корни характеристического уравнения D(s) = 0; s_i = a_i + jw_i. На комплексной плоскости каждый корень может быть представлен вектором (рис. 4.2). Длина вектора 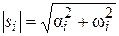, угол поворота от положительной вещественной полуоси равен аргументу Args_i = arctg(w_i/a_i). Отдельные сомножители D(s) вида (s – s_i) могут быть представлены векторами, проведенными из точек s_i в точки s.

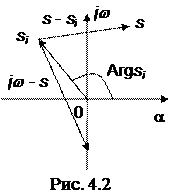Положим s = j w, тогда вектор (s – s_i) = (j w - s_i) будет скользить своим концом по мнимой оси при изменении частоты +¥ £ w £ ¥.

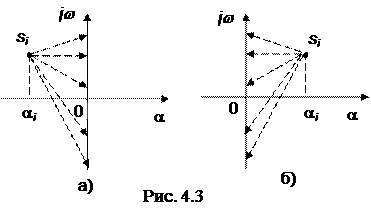
Приращение аргумента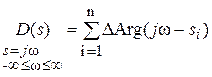, причем корень s_i, расположенный в левой полуплоскости, обеспечивает приращение аргумента +p (рис. 4.3, а), а корень, находящийся в правой полуплоскости, дает DArg s_i =
= -p (рис. 4.3, б).

Если общее число корней характеристического уравнения n, а в правой полуплоскости находится m корней, то суммарное приращение аргумента D (s)

.

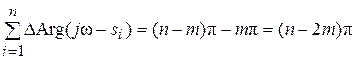Если изменять частоту только в положительном диапазоне 0 £ w £ ¥, то суммарное приращение аргумента D (s) будет в 2 раза меньше

.

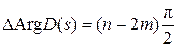Полученное соотношение положено в основу частотных критериев устойчивости непрерывных систем.

Дата добавления: 2014-10-31