Винтовые поверхности

Винтовые поверхности весьма широко используют в техни­ке для формообразования деталей различного назначения.

Винтовая поверхность образуется при движении прямоли­нейной образующей по двум направляющим, одна из которых винтовая линия, другая — ось винтовой линии, которую обра­зующая пересекает под постоянным углом.

Прямая винтовая поверхность. У прямой винтовой поверх­ности угол между образующей и осью равен 90°. Это винто­вой коноид или прямой геликоид. Чертеж прямой винтовой поверхности приведен на рисунке 8.8. Перемещаясь в направ­лении, как указано стрелкой на горизонтальной проекции, отрезок АВ движется вдоль оси вверх и образует правую вин­товую поверхность. Проекции а%Ъ%, a'eb'₆, а'тЬ'-,, a\b'_g, a'_gb'_g условно показаны двумя линиями (они «удаляются» от на­блюдателя).

В сечении прямой винтовой поверхности (рис. 8.9) плоско­стями, перпендикулярными оси или проходящими через ось, получаются отрезки прямолинейной образующей. Используя их, можно построить точки на винтовой поверхности. Так, на ри­сунке 8.9 по горизонтальной проекции а точки А построена ее фронтальная проекция а'на фронтальной проекции образующей Г2' в секущей плоскости Q (Q_h). По фронтальной проекции

4—1340

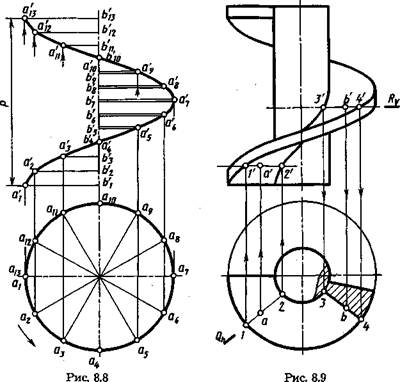
b' точки В построена ее горизонтальная проекция b на горизон­тальной проекции образующей 3—4 в секущей плоскости R (Д,).

Косая винтовая поверхность. Если у винтовой поверхности угол между образующей и осью не равен 90°, то ее назьшают косой винтовой поверхностью. Изображение косой винтовой поверхности — наклонного геликоида приведено на рисун­ке 8.10, а. Проекции отрезка АО — образующей изображены в ряде последовательных положений: от первого до тринадца­того. Точка А образующей перемещается по винтовой линии. Соответствующие положения проекций точки О отмечают на оси, руководствуясь тем, что проекция отрезка АО на ось вра­щения постоянна по величине (/).

Построение сечения косой винтовой поверхности плоско­стью, перпендикулярной оси, показано на рисунке 8.10, б. Такая плоскость пересекает поверхность по кривой линии — спирали Архимеда. Построение сечения выполняют по лини­ям каркаса — точкам С_ь С₂, Q, Q, Q пересечения секущей

а) Рис. 8.Ю б)

плоскости Т (T_v) с образующей винтовой поверхности в ряде последовательных положений 1—О_и, 2—0₂у, З—Оп, 4—0_4и 5—Оц, а также с винтовой линией в точке С₀ (со, с₀). Для построения горизонтальных проекций с_и с₂, с₃, с₄, с₅ точек спирали Архимеда проводят горизонтальные проек­ции образующей винтовой поверхности в ряде произвольных положений: о — 1, о—2, о—З, о — щ, о—5. В проекционной связи на фронтальной проекции винтовой линии отмечают фронтальные проекции Г, 2\ 3\ а\, 5' точек. Через них, учитывая, что величина проекции образующей на ось винто­вой поверхности постоянна (ее значение / отмечено на чер­теже для построения точки о\), строят фронтальные проекции

образующих о\\1\ o\\2\ о'_Ъ\3\ о\а\, о\\5'. В пересечении этих фронтальных проекций с фронтальным следом T_v секу­щей плоскости отмечают фронтальные проекции с\, с г, с'_ъ, с 4, с 5 и по ним в проекционной связи строят горизонталь­ные проекции с\, с₂, с₃, с₄, с₅ искомых точек на соответствую­щих горизонтальных проекциях образующей. Через построенные точки проводят плавную кривую.

Если задана фронтальная проекция произвольной точки М винтовой поверхности, то ее горизонтальную проекцию стро­ят с помощью сечения плоскостью, перпендикулярной оси, как это рассмотрено на рисунке 8.10, б. Если задана горизон­тальная проекция точки (/и), то через нее проводят горизон­тальную проекцию ок образующей, строят фронтальную проекцию о'_кк' по проекции к'тл величине / — проекции обра­зующей на ось винтовой поверхности. На построенной про­екции о ^'образующей отмечают фронтальную проекцию т' точки М.

8.3. Поверхности и тела вращения

в) Рис. 8.11

Поверхности вращения и ограничиваемые ими тела имеют широкое применение во многих областях техники: баллон элек­тронно-лучевой трубки (рис. 8.11, а), центр токарного станка (рис. 8.11, б), объемный сверхвысокочастотный резонатор элек­тромагнитных колебаний (рис. 8.11, в), сосуд Дьюара для хра­нения жидкого воздуха (рис. 8.11, г), коллектор электронов мощного электронно-лучевого прибора (рис. 8.11, д) и т.д.

В зависимости от вида образующей поверхности вращения могут быть ли­нейчатыми, нелинейчатыми или состо­ять из частей таких поверхностей.

Рис. 8.12

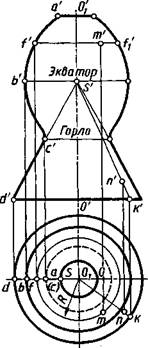
Поверхностью вращения называют поверхность, получающуюся от враще­ния некоторой образующей линии вокруг неподвижной прямой— оси поверхности. На чертежах ось изображают штрихпунк-тирной линией. Образующая линия может в общем случае иметь как кри­волинейные, так и прямолинейные участки. Поверхность вращения на чер­теже можно задать образующей и по­ложением оси. На рисунке 8.12 изоб­ражена поверхность вращения, которая образована вращением образующей ABCD (ее фронтальная проекция a'b'c'd') вокруг оси 00\ (фронталь­ная проекция о 'о 0, перпендикулярной плоскости Н. При вращении каждая точка образующей описывает окруж­ность, плоскость которой перпендику­лярна оси. Соответственно линия пересечения поверхности вра­щения любой плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями. На виде сверху (рис. 8.12) показаны проекции окружностей, опи­сываемых точками А, В, Си D, проходящие через проекции а, Ъ, с, d. Наибольшую параллель из двух соседних с нею параллелей по обе стороны от нее называют экватором, анало­гично наименьшую — горлом.

Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхно­стью вращения — меридианом. Если ось поверхности параллельна плоскости проекций, то меридиан, лежащий в плоскости, параллельной этой плоскости проекций, называют главным меридианом. На эту плоскость проекций главный меридиан проецируется без искажений. Так, если ось поверхности вра­щения параллельна плоскости V, то главный меридиан про­ецируется на плоскость Кбез искажений, например проекция a'f'b'c'd'. Если ось поверхности вращения перпендикулярна

к плоскости Н, то горизонтальная проекция поверхности име­ет очерк в виде окружности.

Наиболее удобными для выполнения изображений поверх­ностей вращения являются случаи, когда их оси перпендику­лярны к плоскости Н, к плоскости Кили к плоскости W.

Некоторые поверхности вращения являются частными слу­чаями поверхностей, рассмотренных в 8.1, например цилиндр вращения, конус вращения. Для цилиндра и конуса вращения меридианами являются прямые линии. Они параллельны оси и равноудалены от нее для цилиндра или пересекают ось в од­ной и той же ее точке под одним и тем же углом к оси для конуса. Цилиндр и конус вращения — поверхности, беско­нечные в направлении их образующих; поэтому на изображе­ниях их ограничивают какими-либо линиями, например линиями пересечения этих поверхностей с плоскостями проек­ций или какими-либо из параллелей. Из стереометрии извест­но, что прямой круговой цилиндр и прямой круговой конус ограничены поверхностью вращения и плоскостями, перпен­дикулярными к оси поверхности. Меридиан такого цилинд­ра — прямоугольник, конуса — треугольник.

Такая поверхность вращения, как сфера, является ограни­ченной и может быть изображена на чертеже полностью. Эква­тор и меридианы сферы — равные между собой окружности. При ортогональном проецировании на все три плоскости про­екций очертания сферы проецируются в окружность.

Тор. При вращении окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, получается поверхность с названием тор. На ри­сунке 8.13 приведены: открытый тор, или круговое кольцо, — рисунок 8.13, а, закрытый тор — рисунок 8.13, б, самопересека­ющийся тор — рисунок 8.13, в, г. Тор (рис. 8.13, г) называют также лимоновидным. На рисунке 8.13 они изображены в по­ложении, когда ось тора перпендикулярна к плоскости про­екций Н. В открытый и закрытый торы могут быть вписаны сферы. Тор можно рассматривать как поверхность, огибаю­щую одинаковые сферы, центры которых находятся на ок­ружности.

В построениях на чертежах широко используют две системы круговых сечений тора: в плоскостях, перпендикулярных к его оси, и в плоскостях, проходящих через ось тора. При этом в плоско-

а) 6) д} г)

Рис. 8.13

стях, перпендикулярных к оси тора, в свою очередь имеются два семейства окружностей — линий пересечения плоскостей с наружной поверхностью тора и линий пересечения плоскостей с внутренней поверхностью тора. У лимоновидного тора (рис. 8.13, г) имеется только первое семейство окружностей.

Кроме того, тор имеет еще и третью систему круговых сече­ний, которые лежат в плоскостях, проходящих через центр тора и касательных к его внутренней поверхности. На рисунке 8.14 показаны круговые сечения с центрами o_ip и о_2р на дополни­тельной плоскости проекций Р, образованные фронтально-про­ецирующей плоскостью Q (Q_v), проходящей через центр тора с проекциями о", о и касательной к внутренней поверхности тора в точках с проекциями Г, 1, 2", 2. Проекции точек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10 облегчают чтение чертежа. Диаметр d этих круговых сечений равен длине больших осей эллипсов, в которые проецируются круговые сечения на горизонтальной плоскости проекций: d=2R.

Точки на поверхности вращения. Положение точки на по­верхности вращения определяют по принадлежности точки ли­нии каркаса поверхности, т. е. с помощью окружности, проходящей через эту точку на поверхности вращения. В слу­чае линейчатых поверхностей для этой цели возможно приме­нение и прямолинейных образующих.

Применение параллели и прямолинейной образующей для построения проекций точек, принадлежащих данной поверхности вращения, показано на рисунке 8.12. Если

Дата добавления: 2014-11-06