КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольной работы. Методические рекомендации для выполнения
|
|
|
|
Методические рекомендации для выполнения
Тема «Элементы линейной алгебры»
Знакомство с использованием определителей начните с простейшего случая решения и исследования системы двух линейных уравнений с двумя неизвестными. Изучите свойства определителя второго, а затем третьего порядка.
Особое внимание обратите на то, что вычисление определителей упрощается, если умело пользоваться свойствами определителей.
При изучении вопросов, связанных с исследованием систем линейных алгебраических уравнений, не упустите из виду случай, когда главный определитель системы равен нулю. В этой ситуации формулы Крамера теряют смысл и соответствующие системы уравнений либо несовместны, либо имеют бесчисленное множество решений.
Пример №1: Используя формулы Крамера, решить систему и сделать проверку.
 x – 2y + z = 4,
x – 2y + z = 4,
2x + y + 3z = 5
3x + 4y+ z = –2.
Подсчитаем главный определитель системы D, используя правило вычисления определителей третьего порядка.
Имеем:

 1 –2 1
1 –2 1
D = 2 1 3 = 1* (1–12) + 2 * (2 – 9) +1 * (8 – 3) = – 20.
3 4 1
Так как D ≠ 0, то система имеет единственное решение. Для его отыскания вычислим вспомогательные определители: Dх, Dу, Dz.

 4 –2 1
4 –2 1
Dx = 5 1 3 = 4 * (1 -12) – (–2) * (5+6) +1 * (20+2) = 0;
–2 4 1

 1 4 1
1 4 1
Dy = 2 5 3 = 1*(5 + б) – 4*(2 – 9) + 1*(– 4 – 15) = 20;
3 -2 1

 1 -2 4
1 -2 4
Dz = 2 1 5 = 1*(−2 – 20) – (– 2) *(–4 –15) + 4*(8 – 3) = – 40.
3 4 –2
Найдем неизвестные по формуле Крамера:
x = 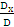 = 0; y =
= 0; y =  = – 1; z =
= – 1; z = 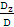 = 2.
= 2.
Проверка осуществляется путем подставления полученного решения в каждое уравнение системы:
 0 – 2 *(–1) + 2 = 4
0 – 2 *(–1) + 2 = 4
2*0 + (–1) + 3*2 = 5
3*0 + 4*(–1) +2 = -2
Все три равенства верные, следовательно, ответ имеет вид(0; –1; 2).
Тема «Элементы аналитической геометрии»
При изучении этой темы, прежде всего, следует усвоить понятие уравнения линии. Подобно тому, как точка в аналитической геометрии определяется координатами, линия определяется уравнением, связывающим координаты любой точки этой линии. Прямая линия является простейшей из линий на плоскости. Изучите различные способы нахождения уравнения прямой, а также плоскости.
|
|
|
Успех решения задач во многом зависит от умелого выбора соответствующего вида уравнения прямой и плоскости.
Пример №1:
Даны координаты вершин треугольника ABC: A(-1;2), В(5;-1), С(-4;-5).
 1) Расстояние l между точками M1 (х1;у1) и М2 (х2;у2) находим по формуле: l = |М1 М2| =
1) Расстояние l между точками M1 (х1;у1) и М2 (х2;у2) находим по формуле: l = |М1 М2| = 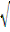 (x2 – х1)2 + (у2 – у1)2.
(x2 – х1)2 + (у2 – у1)2.
По этой формуле находим длину стороны АВ:
 AB| =
AB| = 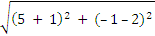 =
=  = 3
= 3  .
.
2) Уравнение прямой, проходящей через две точки плоскости M1 (x1; y1) и М2 (х2; у2) имеет вид
 (1)
(1)
Подставляя в это уравнение координаты точек А и В, получаем уравнение стороны АВ:

Угловой коэффициент kАB прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом у = kx + b.
Получим: 2у = -х+3 => y= – 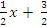 .
.
Следовательно, kAB = –  .
.
Аналогично находим: kBC =  .
.
3) Для нахождения внутреннего угла треугольника ABC воспользуемся формулой: tgB =  .
.
Отметим, что порядок разности угловых коэффициентов, стоящей в числителе дроби, зависит от взаимного расположения прямых АВ и ВС. Подумайте, как бы вы стали искать внутренние углы А и С треугольника ABC?
Подставим значения kАВ и kвс в формулу. Находим:
tgB = 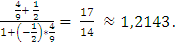
По таблицам В.М. Брадиса или на инженерном микрокалькуляторе получаем  B
B  50°.
50°.
|
XM = 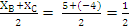
yM = 
Теперь подставим в (1) координаты точек А и М, получаем уравнение медианы:
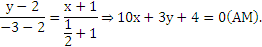
5) Для составления уравнения высоты CD, воспользуемся уравнением прямой, проходящей через точку M0 (x0; y0) с заданным угловым коэффициентом k, которое имеет вид
y − yo= k*(x - xo) (2)
и условием перпендикулярности АВ и CD, которое выражается соотношением
|
|
|
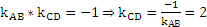 .
.
Подставим в (2)  получим уравнение высоты СD:
получим уравнение высоты СD:  (CD).
(CD).
Используя полученные результаты, начертим треугольник АВС на координатной плоскости:
 |
Тема «Вычисление пределов»
При изучении этой темы следует обратить внимание на понятие функции и изучить ее свойства. Познакомиться со всеми элементарными функциями (линейными, степенными, показательными, логарифмическими, тригонометрическими).
Особое внимание уделить пределу функции в точке и на бесконечность и понятию непрерывной функции.
После подробного изучения свойств пределов, I и II замечательных пределов, следует приступить к непосредственному вычислению пределов элементарных функций и их композиций, учитывая, что под знаком предела можно производить тождественные преобразования выражения.
Пример №1. Вычислить предел: 
Пример №2. Вычислить предел: 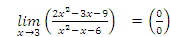
Решение: т.к.

 ,
, 
то
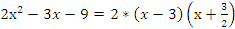

Следовательно, 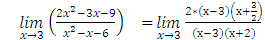 =
= 
Пример №3.
Вычислить предел:  =
= 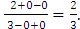
Тема «Дифференциальное исчисление функций одной переменной»
В основе этой темы лежит понятие производной. Особое внимание следует обратить на геометрическое и механическое истолкование производной. Особую роль при решении задач играет правило вычисления производной сложной функции.
При дифференцировании некоторых функций нередко значительно упрощает вычисление прием, состоящий в том, что перед вычислением производной функцию предварительно логарифмируют.
При решении всех последующих примеров, кроме таблицы производных, используются правила дифференцирования суммы, разности, произведения, частного и теорема о производной сложной функции:
a) 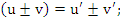
б)  ;
;
в) 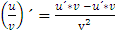 ;
;
г) 
Пример№1. Дана функция: y =  .
.
Вычислить производную функции.
Решение:
y´= 
= 
=  .
.
Пример№2. Дана функция: 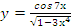
Вычислить производную функции.
Решение:
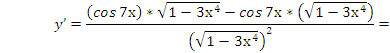



Пример №3. Дана функция: 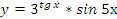 .
.
Вычислить производную функции.
Решение:


Тема «Исследование функции одной переменной»
Изучение этой темы следует начать с усвоения понятий возрастания и убывания функции, максимума и минимума функции, выпуклости и вогнутости кривой.
Пример:
1) Исследовать функцию у =  (х3 + 9х2 +15х - 9) и построить график.
(х3 + 9х2 +15х - 9) и построить график.
|
|
|
Решение:
1) D (x) = (-∞;+∞), т.е. функция непрерывна на всей числовой прямой.
2)Для исследования функции на экстремумы и монотонность необходимо найти производную и приравнять ее к нулю.
Имеем: y´ =  (3x2+9*2x + 15 − 0)
(3x2+9*2x + 15 − 0)
у' = 0 => 3х2+18х + 15= 0
х2+6х + 5 = 0
х1 = -5; х2 = -1
| х | (-∞,-5) | -5 | (-5;-1) | -1 | (-1;+∞) |
| f´(х) | + | 0 | − | 0 | + |
| f (x) | ↗ 
| max | ↘ | min | ↗ |
у max (-5)=  ((-5)3+9*(-5)2 +15*(-5) − 9) =4
((-5)3+9*(-5)2 +15*(-5) − 9) =4
у min (-1) = 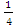 ((-1)3 +9*(-1)2+15*(−1)−9) =−4
((-1)3 +9*(-1)2+15*(−1)−9) =−4
3) Для определения точек перегиба и интервалов вогнутости и выпуклости найдем вторую производную и приравняем ее к нулю.
Имеем: y ´´ = 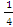 (3 * 2 *x + 18+0)
(3 * 2 *x + 18+0)
6х + 18 = 0
х + 3 = 0
х = -3
| х | (-∞; -3) | -3 | (-3;+∞) |
| f ´(х) | - | 0 | + |
| f (x) | ∩ | точка перегиба | ∪ |
у(-3) =  ((-3)3 + 9(-3)2 + 15(−3) − 9) = 0.
((-3)3 + 9(-3)2 + 15(−3) − 9) = 0.
Точка (-3,0) - точка перегиба.
Используя полученные результаты исследования, построим график функции.

Тема «Интегралы»
Прежде чем приступить к интегрированию функций, тщательно изучите таблицу интегралов, свойства определенного интеграла и два простейших метода интегрирования: метод замены переменной и способ подстановки. Успех интегрирования в значительной степени зависит от того, сумеем ли мы подобрать удачную замену переменной, упрощающую данный интеграл.
При использовании метода интегрирования по частям очень важно правильно выбрать множители U и dv. Хотя общих правил разбиения нет, тем не менее, можно руководствоваться некоторыми частными правилами. Например, если подынтегральная функция представляет собой произведение показательной или тригонометрической функции и многочлена, то в качестве множителя U следует выбирать многочлен. Если же подынтегральная функция является произведением логарифмической или обратной тригонометрической функций и многочлена, то в качестве множителя U следует выбрать логарифмическую или обратную тригонометрическую функцию.
При интегрировании выражения, содержащего в знаменателе квадратный трехчлен, целесообразно привести этот трехчлен к виду с выделенным полным квадратом.
Пример№1. Найти интеграл: ∫(5 − 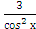 +2
+2  )dх.
)dх.
|
|
|
Решение: Воспользуемся таблицей интегралов и основными свойствами первообразной:
∫(5 − 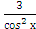 +2
+2  )dх = 5∫dх − 3∫
)dх = 5∫dх − 3∫  dх+2∫
dх+2∫  dх =
dх =
= 5х − 3tgх + 2 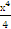 +с = 5х −3tgх +
+с = 5х −3tgх +  +с.
+с.
Пример №2. Найти интеграл: ∫ 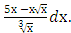
Решение: Воспользуемся определением степени с дробным показателем ( =
=  , а > 0), правилами действий со степенями с одинаковыми основаниями (аn am = an+m,
, а > 0), правилами действий со степенями с одинаковыми основаниями (аn am = an+m, 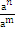 =
=  ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно.
), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно.
∫ 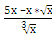 dх = ∫
dх = ∫ 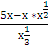 dх= ∫
dх= ∫  dх − ∫
dх − ∫ 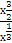 dх =
dх =
= 5∫х  dх − ∫х
dх − ∫х  dх = 5
dх = 5 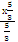 −
−  +с = 3
+с = 3 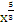 −
−  +с =
+с =
= 3* 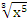 −
− 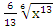 +с.
+с.
Пример №3. Найти интеграл: ∫ 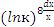 .
.
Решение: Применим подстановку: t = 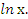
Тогда dt =  .
.
Имеем: ∫ ( = ∫
= ∫  dt =
dt = 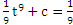 (
(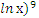 + c.
+ c.
Пример №4. Найти интеграл:
∫ 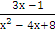 dх.
dх.
Решение: Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:
х2 − 4х + 8 = х2 + 4 +7 = (х − 2)2 + 22.
Тогда после подстановки t= х−2 получаем:
∫ 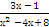 dх = ∫
dх = ∫  dх =∫
dх =∫  dt = ∫
dt = ∫ 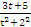 dt =
dt =
= ∫  dt +∫
dt +∫  dt =
dt = 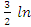 (t2+4) +
(t2+4) +  actg
actg  +c =
+c =
 (х − 2
(х − 2 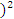 +4) +
+4) +  actg
actg  +c =
+c =
=  (х2 − 4х +8) +
(х2 − 4х +8) +  actg
actg  + с.
+ с.
При этом при вычислении интеграла ∫  dt мы воспользовались заменой переменной z = t2 +4.
dt мы воспользовались заменой переменной z = t2 +4.
Тогда dz = 2tdt, откуда
∫ 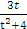 dt =
dt =  ∫
∫  =
=  ∫
∫  =
= 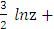 c =
c = 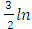 (
( +4) +c.
+4) +c.
Пример №5. Найти интеграл: ∫(2х + 8)* 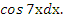
Решение: Применим формулу интегрирования по частям: ∫udv=uv − ∫vdu.
Положим: u = 2х +8, dv = 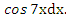
Тогда: du = 2dх, v = ∫  =
= 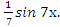
Следовательно: ∫(2х + 8)  −
− 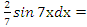
 +
+ 
Пример №6. Найти интеграл: ∫actg3х*dх.
Решение: Положим u = actg3х, dv = dх, тогда du = 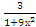 , v = х.
, v = х.
Отсюда: ∫actg3хdх = х* actg3х −3∫ 
Применим в последнем интеграле подстановку t = 1+9 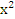 , получим dt=18хdх, следовательно: 3∫
, получим dt=18хdх, следовательно: 3∫ 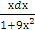 =
=  ∫
∫  =
= 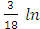 (1+9
(1+9  )+с.
)+с.
Отсюда: ∫actg3хdх = х* actg3х − 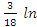 (1+9
(1+9 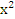 )+с.
)+с.
Критерий оценивания знаний студента на экзамене
1. Оценка «отлично» ставится за полный ответ на теоретические вопросы и за правильное решение упражнения в приложении.
2. Оценка «хорошо» ставится в том случае, если при ответе на теоретические вопросы имелись неточности, которые не указывают на непонимание студентом сути вопроса, или, в случае ответа на теоретические вопросы, в упражнениях были сделаны ошибки, которые привели к неверному результату, но способ решения был выбран верно.
3. Оценка «удовлетворительно» ставится тогда, когда есть ответ на один теоретический вопрос и решение упражнения, при этом студент не отвечает на наводящие вопросы по неподготовленному теоретическому вопросу.
Возможно выставление оценки «удовлетворительно» и в том случае, когда оба ответа на теоретические вопросы содержат существенные погрешности, которые студент с помощью преподавателя может устранить, демонстрируя при этом умение решать типовые примеры, студент должен знать основные понятия.
4. Оценка «неудовлетворительно» ставится при отсутствии ответов на оба теоретических вопроса или у студента отсутствуют практические навыки.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 297; Нарушение авторских прав?; Мы поможем в написании вашей работы!