Тема 3. Решение систем линейных уравнений

3.1. Метод обратной матрицы

Пример. Решить систему уравнений: .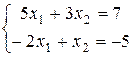

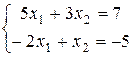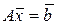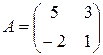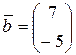1. Запишем систему в матричном виде: вместо имеем , где ; ; , то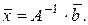

2. Найдем обратную матрицу:

.

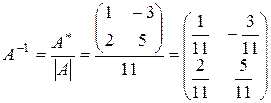3. Вычисляем искомый вектор:

,

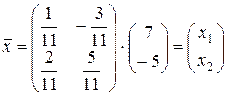где

,

.

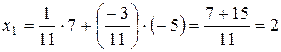Сделаем проверку, подставив полученный результат в данную систему:

.

.

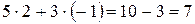3.2. Метод Гаусса

Рассмотрим систему m уравнений,связывающих n неизвестных

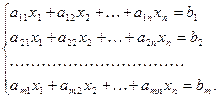(1)

Здесь a_ij (1≤i≤m, 1≤j≤m) коэффициенты; b_j – cвободные члены. Если все коэффициенты и свободный член какого- то уравнения равны нулю, то вычеркиваем его из системы. Если коэффициенты при всех неизвестных равны нулю, а b≠0, то система решений не имеет.

Условимся,что первым в системе (1) стоит уравнение, в котором коэффициент при первом неизвестном отличен от нуля (например а₁₁≠0). Запишем систему (1) в виде матрицы опустив неизвестные и отделяя свободные члены вертикальной чертой

(2)

Делим все элементы первой строки на

(3)

Затем из каждой 2-й,3-й,...,m-й строки матрицы (3) вычитаем почленно первую строку умноженной соответственно на a_21,a₃₁,..,a_m1; при этом результат вычитания получится в виде

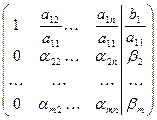(4)

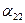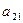
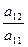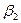где = - ,..., =b₂ – .

Повторяя указанную операцию необходимое число раз,получим матрицу вида

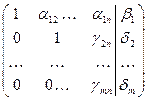(5)

Полученной матрице соответствует система уравнений

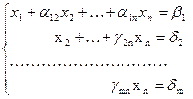(6)

Пользуясь тем,что система имеет треугольный вид,ее можно решать последовательно, начиная с последнего уравнения.

Пример. Решить систему линейных уравнений методом Гаусса

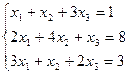(7)

Матрица этой системы имеет вид

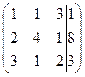(8)

Первую строку матрицы (8) умноженную на 2 и на 3 вычитаем из второй и третьей, соответственно

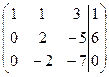( (9)

Далее, к третьей строке матрицы (9) прибавив вторую, получим матрицу

соответствующей системе

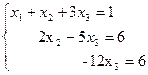
Значит, решением системы (7) будет

, .

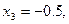
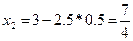Дата добавления: 2014-11-09