Определение производной функции

Вопросы лекции.

Тема лекции. Производная и дифференциал функции.

Лекция № 4.

1. Определение производной функции.

2. Правила нахождения производных. Таблица производных.

3. Дифференциал функции.

Производная функции используется для решения многих задач, в особенности при изучении скорости разных процессов, в том числе и экономических.

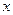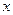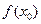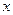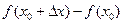Пусть имеем некоторую функцию , определенную на некотором промежутке. Рассмотрим два значения аргумента: исходное и новое . Разность называется приращением аргумента в точке . Отсюда получаем, то - есть первоначальное значение переменной получило некоторое приращение. Тогда, если в точке значение функции было , то в новой точке функция будет принимать значение . Разность называется приращением функции в точке и обозначается символом .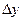

Производнойфункции в точке называется предел отношения приращения функции к приращению аргумента в этой точке, когда приращение аргумента стремится к нулю

Функция , имеющая производную в каждой интервала, называется дифференцируемой в этом интервале. Операция нахождения производной от данной функции называется дифференцированием этой функции. В результате дифференцирования получается некоторая функция, обозначаемая . Также производная функции обозначается 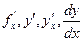. Конкретное значение производной функции в точке 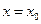обозначаются .

Для функции 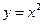найдем ее производную по определению и значение производной этой функции в точке 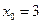. Аргументу 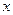даем приращение . Находим приращение функции . Определяем отношение . Находим предел этого отношения, когда : 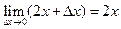. Итак 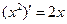. Значение производной функции 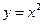в точке 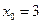равно .

Производная от первой производной называется производной второго порядка или второй производной от данной функции и обозначается или 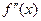. Итак . Аналогично определяется производная любого порядка.

Пусть функция , описывает какой – либо физический процесс, тогда производная есть скорость изменения этого процесса, а вторая производная – ускорение. В этом состоит физический смысл производной.

В экономических исследованиях для обозначения производных часто пользуются специальной терминологией. Например, если есть производственная функция, выражающая зависимость выпуска какой-либо продукции от затрат фактора 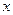, то называют предельным продуктом; если 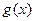есть функция издержек, то естьвыражает зависимость общих затрат от объема продукции 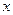, то называют предельными издержками.

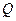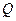
Пусть = - количество произведенной продукции 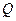за время t. Тогда P есть производительность труда P в момент времени , а 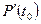есть скорость изменения производительности труда в момент времени .

Во многих задачах часто требуется вычислять процент прироста зависимой переменной, соответствующий проценту прироста независимой переменной. Это приводит к понятию эластичности функции. Эластичность E функции вычисляют по формуле . Эластичность функции показывает, на какое количество процентов изменится значение функция при изменении аргумента 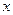на 1 %.

Уравнение касательной к графику функции в точке касания имеет вид . Таким образом, геометрически 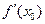представляет угловой коэффициент касательной к графику этой функции в точке , в этом состоит геометрический смысл производной.

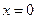Отмети также, что если функция дифференцируема в некоторой точке , то она в этой точке непрерывна. Обратное утверждение не верно, так функция непрерывна в точке , но не дифференцируема в ней.

Дата добавления: 2014-11-26