Решение. Пределом функции в точке называется такое число , что для любой последова

Решение.

Предел функции.

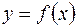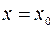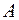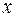Пределом функции в точке называется такое число , что для любой последовательности значений аргумента , сходящейся к числу , последовательность 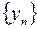, 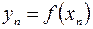соответствующих значений функции стремится к этому числу 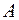и обозначается: .

При нахождении пределов функций нужно использовать следующие свойства предела функции: если существуют конечные пределы 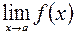и , то

1) ;

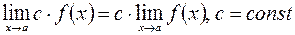2) ;

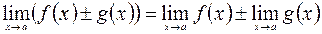3) ;

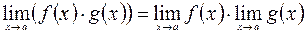4) 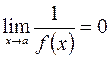(или ), если 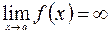(или 0);

5) , если .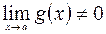

Пример. Вычислить .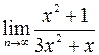

Решение: Разделим числитель и знаменатель на , получим:

.

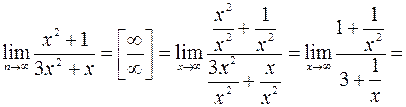
При нахождении пределов функций также полезно знать первый замечательный предел: и следствия из него:

; ; ;

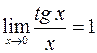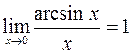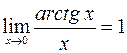и второй замечательный предел: .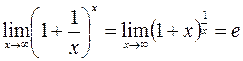

Пример. Вычислить предел .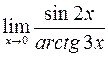

.

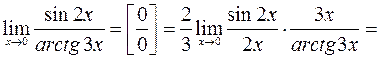
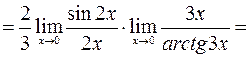
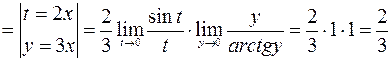Пример. Вычислить предел .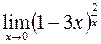

.

Общий метод (правило Лопиталя) вычисления пределов в случаях неопределенности и 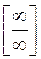рассматривается в дифференциальном исчислении.

Пусть 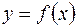функция от 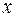, имеющая пределом число 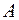, когда 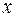стремится к числу 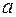. Предположим, что все значения величины 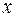меньше, чем число 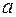, то есть 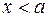. Символически это выражается очень удобной записью: 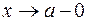(вместо 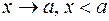). Тогда предел 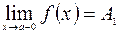называют пределом функции 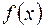в точке 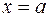слева или левосторонним пределом.

Аналогично, при , то есть 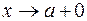предел 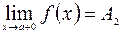называют пределом функции 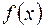в точке 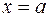справа или правосторонним пределом.

Левосторонний и правосторонний пределы функции в точке называются односторонними пределами.

Дадим определение непрерывности функции в точке.

Функция 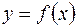называется непрерывной в точке 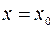, если:

1) функция 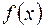определена в точке и в некоторой ее окрестности, содержащей эту точку ;

2) функция 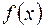имеет одинаковые односторонние пределы в этой точке , то есть ;

3) эти односторонние пределы должны быть равны значению функции 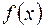в этой точке : .

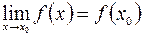Функция 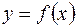называется разрывной в точке 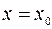, если она определена в сколь угодно малой окрестности точки , но в самой точке не удовлетворяет хотя бы одному из условий непрерывности.

Точки разрыва функции можно разделить на два типа.

Точка разрыва функции 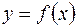называется точкой разрыва 1-го рода, если существуют конечные односторонние пределы функции в этой точке, которые не равны между собой или равны между собой, но не равны значению функции в этой точке. Если хотя бы один из односторонних пределов функции в точке не существует или равен бесконечности, то – точка разрыва функции 2-го рода.

Пример. Исследовать на непрерывность функцию и построить ее график .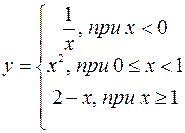

Решение. Областью определения данной функции является вся числовая ось, то есть 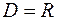. Точками «подозрительными» на точки разрыва являются точк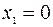и и , так как при переходе через эти точки функция меняет свое аналитическое выражение с дробно – рациональной на квадратичную и с квадратичной на линейную, соответственно.

Исследуем непрерывность функции в точке :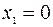

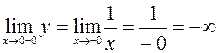
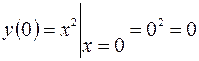
Поскольку условие непрерывности функции в точке 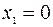нарушается, то 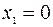– точка разрыва функции , т.к. левосторонний предел функции в точке 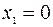равен бесконечности, то 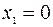– точка разрыва 2-го рода.

Исследуем непрерывность функции в точке :

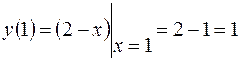
Условие непрерывности функции в точке выполняется, значит, функция в точке непрерывна.

Построим график функции :

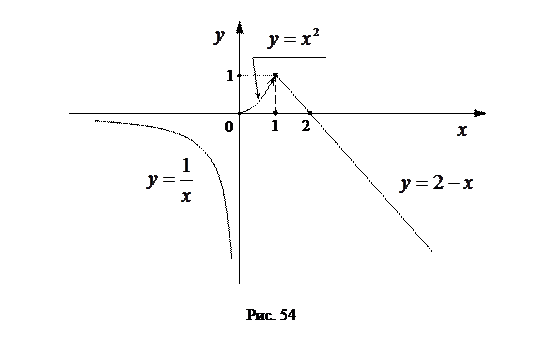
Дата добавления: 2014-11-09