
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кореляційний і регресійний методи аналізу зв’язку
|
|
|
|
Основне завдання кореляційного і регресійного аналізу статистичних даних є виявлення залежності між досліджуваними ознаками у вигляді певної математичної формули й установлення за допомогою коефіцієнта кореляції тісноти взаємозв’язку.
Кореляційний і регресійний методи аналізу вирішують два основних завдання:
1) визначають за допомогою рівняння регресії аналітичну форму зв’язку між варіацією ознак х і у;
2) установлюють ступінь тісноти зв’язку між ознаками.
На практиці економіко-статистичних досліджень часто доводиться мати справу з прямолінійною формою зв’язку, яка виражається за допомогою рівняння регресії.
Рівняння регресії характеризує зміну середнього рівняння результативної ознаки у в залежності від зміни факторної ознаки х.
У випадку лінійної форми зв’язку рівняння регресії має вид:

де  – вирівняне середнє значення результативної ознаки;
– вирівняне середнє значення результативної ознаки;
х – значення факторної ознаки;
а 0, а 1 – параметри рівняння регресії;
а 0– значення у при х = 0;
а 1 – коефіцієнт регресії.
Коефіцієнт регресії а 1 показує наскільки зміниться результативна ознака у при зміні факторної ознаки х на одиницю.
Якщо а 1 має позитивний знак, то зв'язок прямий, якщо від’ємний – зв'язок обернений.
Параметри рівняння зв’язку визначаються методом найменших квадратів складеної і розв’язаної системи двох рівнянь з двома невідомими.
 ,
,
де п – число одиниць спостереження у кожному з двох порівнюваних рядів;
Σ х – сума значень факторної ознаки;
Σ у – сума значень результативної ознаки;
Σ ху – сума добутків значень факторної ознаки на значення результативної ознаки.
Розв’язавши дану систему рівнянь, отримаємо такі значення параметрів рівняння регресії:
|
|
|
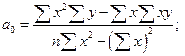

Вирахувавши за фактичними даними всі записані вище суми і підставивши їх у наведені формули, знайдемо параметри шуканої прямої (табл. 8.8).
Таблиця 8.8 – Розрахунок параметрів лінійного рівняння зв’язку і
лінійного коефіцієнта кореляції між вартістю основних
виробничих фондів і випуском продукції
| Номер підприємства | Вартість основних виробничих фондів, млн. грн. (х) | Випуск продукції, млн. грн. (у) | Розрахункові графи | |||

| 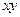
| 
| 
| |||
| 5,6 | 67,2 | 31,36 | 5,2 | |||
| 4,0 | 32,0 | 16,0 | 3,5 | |||
| 4,0 | 40,0 | 16,0 | 4,4 | |||
| 2,4 | 14,4 | 5,76 | 2,7 | |||
| 3,6 | 32,4 | 12,96 | 4,0 | |||
| 5,0 | 75,0 | 25,0 | 6,5 | |||
| 4,6 | 50,6 | 21,16 | 4,8 | |||
| 6,5 | 84,5 | 42,25 | 5,6 | |||
| 7,0 | 98,0 | 49,0 | 6,1 | |||
| 4,5 | 45,0 | 20,25 | 4,4 | |||
| Разом: | 47,2 | 539,1 | 239,74 | 47,2 | ||
| В середньому на одне підприємство | 10,8 | 4,72 | 123,6 | 53,91 | 23,974 | 4,72 |
За методом найменших квадратів визначаємо параметри лінійного рівняння регресії:
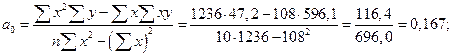

Лінійне рівняння регресії між вартістю основних виробничих фондів та випуском продукції має вид:  = 0,167 + 0,421 х.
= 0,167 + 0,421 х.
Таким чином, при збільшенні вартості основних виробничих фондів на 1 млн.грн. випуск продукції зросте на 0,421 млн.грн.
Підставляючи в дане рівняння послідовно значення факторної ознаки х, отримаємо вирівняні значення результативної ознаки у. Якщо параметри рівняння визначені правильно, то ∑ у = ∑ 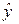 = 47,2.
= 47,2.
Побудуємо графік, який покаже вирівнювання емпіричних даних рівнянням прямої.


Рисунок 8.2 – Емпіричні і вирівняні рівні ряду
Для економічної інтерпретації лінійних і нелінійних зв’язків між двома досліджуваними явищами часто використовують розраховані на основі рівнянь регресії коефіцієнти еластичності.
Коефіцієнт еластичності (ε) показує, на скільки відсотків змінюється в середньому результативна ознака у при зміні факторної ознаки х на 1 %.
|
|
|
Для лінійної залежності коефіцієнт еластичності визначається за формулою:
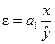 ,
, 
де ε– коефіцієнт еластичності.
У даному прикладі коефіцієнт еластичності на першому підприємстві при (х =12) буде дорівнювати:
 .
.
Отже, на 1 % приросту вартості основних виробничих фондів, випуск продукції зросте на 0,97 %.
На п’ятому підприємстві при (х = 9)  ,
,
на десятому – при (х = 10)  .
.
Для всіх підприємств сумарний коефіцієнт еластичності становить:

Це означає, що при збільшенні середньої вартості основних виробничих фондів на 1 % випуск продукції зросте в середньому на 0,963 %.
Якщо залежність між ознаками параболічна, то коефіцієнт еластичності визначається за формулою:

Визначення тісноти зв’язку в кореляційно-регресійному аналізі ґрунтується на правилі складання дисперсій, але для оцінки лінії регресії використовують теоретичні значення результативної ознаки.
Різниця між загальною і залишковою дисперсіями дає нам теоретичну (факторну) дисперсію, яка вимірює варіацію, зумовлену фактором х. На порівнянні цієї різниці із загальною дисперсією побудований індекс кореляції, або теоретичне кореляційне відношення (R), які обчислюються за формулами:
 або
або 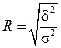 ,
,
де R – індекс кореляції (теоретичне кореляційне відношення);
σ2 – загальна дисперсія;
σ е 2 – залишкова дисперсія;
δ2 – факторна (теоретична) дисперсія.
Факторну дисперсію з теоретичних значень обчислюють за формулою:

Залишкову дисперсію визначають за формулою:

або за правилом складання дисперсій:  .
.
У даному прикладі факторна дисперсія дорівнює:

Загальна дисперсія становить:
 .
.
Залишкову дисперсію визначаємо як різницю між загальною і факторною дисперсіями:
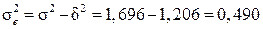 .
.
Таким чином, індекс кореляції за вищенаведеними формулами буде дорівнювати:
 ,
,
або 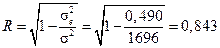 ,
,
або  .
.
Індекс кореляції показує тісну залежність випуску продукції від вартості основних фондів.
Коефіцієнт детермінації (R 2) характеризує ту частину варіації результативної ознаки у, яка відповідає лінійному рівнянню регресії:
 .
.
Отже, у досліджуваній сукупності підприємств 71,1 % варіації випуску продукції пояснюється різними рівнями оснащеності заводів основними виробничими фондами.
Індекс кореляції набуває значення від 0 до 1.
|
|
|
Коли R = 0, то між варіацією ознак у і х зв’язку немає. Залишкова дисперсія дорівнює загальній –  , а теоретична дисперсія дорівнює нулю
, а теоретична дисперсія дорівнює нулю  .
.
При R = 1 теоретична дисперсія дорівнює загальній –  , а залишкова –
, а залишкова –  .
.
Для вимірювання тісноти зв’язку і визначення його напряму за лінійної залежності використовують лінійний коефіцієнт кореляції (r), який визначається за формулою:
 .
.
Для спрощення розрахунків лінійного коефіцієнта кореляції використовують перетворену формулу:
 .
.
Значення r коливається в межах від -1 до +1. Додатне значення r означає прямий зв'язок між ознаками, а від’ємне – зворотній. Оцінка тісноти зв’язку відбувається за схемою (табл. 8.9).
Таблиця 8.9 – Шкала щодо оцінки тісноти та напряму зв’язку між ознаками
| Сила зв’язку | Величина лінійного коефіцієнта кореляції за наявності: | |
| прямого зв’язку | оберненого зв’язку | |
| Слабка | 0,1 – 0,30 | (-0,1) – (-0,30) |
| Середня | 0,3 – 0,70 | (-0,3) – (-0,70) |
| Тісна | 0,7 – 0,99 | (-0,7) – (-0,99) |
За даними нашого прикладу обчислимо лінійний коефіцієнт кореляції:
 ;
;
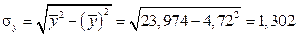 ;
;
 .
.
Це означає, що зв'язок між вартістю основних виробничих фондів і випуском продукції сильний (тісний) і прямий.
Суттєвість зв’язку коефіцієнта детермінації R 2 перевіряють за допомогою таблиці критерію F для 5-відсоткового рівня значимості. Так, при k 2 = n – m =
= 10 – 2 = 8. Фактичне значення F -критерію для нашого прикладу визначають за формулою [20]:
 .
.
Критичне значення F Т(0,95) значно менше від фактичного F Т(0,95) < F Ф (5,32 < 19,68), що підтверджує суттєвість кореляційного зв’язку між досліджуваними ознаками.
Для установлення достовірності обчисленого лінійного коефіцієнта кореляції використовують критерій Стьюдента (t -критерій):  ,
,
де 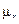 – середня помилка коефіцієнта кореляції, яку визначають за формулою:
– середня помилка коефіцієнта кореляції, яку визначають за формулою:
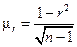 .
.
За достатньо великого числа спостережень (п > 50) коефіцієнт кореляції можна вважати достовірним, якщо він перевищує свою помилку в 3 і більше разів, а якщо він менше 3, то зв'язок між досліджуваними ознаками у і х не доведений.
У нашому прикладі середня помилка коефіцієнта кореляції дорівнює:
|
|
|
 .
.
Відношення коефіцієнта кореляції до його середньої помилки становить:
 .
.
Це дає нам право вважати, що обчислений лінійний коефіцієнт кореляції достатньо точно характеризує силу зв’язку між досліджуваними ознаками.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 730; Нарушение авторских прав?; Мы поможем в написании вашей работы!