Элементы аналитической геометрии и векторной алгебры

Задачи для контрольных заданий

Тема XII. Элементы математической статистики.

1. Что называется выборкой? Напишите формулу для вычисления выборочной средней.

2. Какие оценки называются точечными? Дайте определения не­смещенной и состоятельной оценок.

3. Какие оценки являются интервальными? В каких случаях следует использовать интервальную оценку?

4. Для чего служит метод наибольшего правдоподобия? Как им пользоваться для дискретных и непрерывных случайных величин?

5. Как найти доверительные интервалы для оценки математического ожидания нормального распределения?

6. Дайте определение статистической гипотезы, приведите примеры статистической проверки гипотез.

Литература

1. Ильин В.А., Позняк Э.Г.. Аналитическая геометрия.— М.: Наука, 1981.

2. Ефимов Н.В. Краткий курс аналитической геометрии. — М.: Наука, 1967.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.— М.: Высшая школа, 1967-1971. Ч. I, II, III.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов.— М.: Наука, 1970—1985, т. 1, 2.

5. Шкіль М.І., Колесник Т.В., Котлова В.М.. Вища математика.– К.: Либідь, 1994. Т. 1-3.

6. Мышкис А.Д. Лекции по высшей математике — М.: Наука, 1967.

7. Привалов И.И. Аналитическая геометрия.— М., 1956.

8. Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах.— М.: Высшая школа, 1985.

9. Каплан И.А. Практические занятия по высшей математике. – Харьков, 1967.

10. Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики.— М.: Высшая школа, 1987.

11. Бермант А.Ф., Абрамович И.Г. Краткий курс математического анализа.— М.: Наука, 1973.

12. Мантуров О.В., Матвеев Н.М. Курс высшей математики.— М.: Высшая школа, 1986.

13. Самойленко А.М., Перестюк М.О., Парасюк І.О. Диференціальні рівняння.— К.: Либідь, 1994.

14. Запорожец Г.И. Руководство к решению задач по математическому анализу.— М.: Высшая школа, 1966.

15. Гмурман В.Е. Теория вероятностей и математическая статистика.— М.: Высшая школа, 1972.

16. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.— М.: Высшая школа, 1975.

17. Гурский Е.И. Теория вероятностей с элементами математической статистики. – М.: Высшая школа, 1971.

18. Вентцель Е.С., Овчаров Л.А. Теория вероятностей. Задачи и упражнения.— М.: Наука, 1969.

19. Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М. Высшая математика. — К.: Вища школа, 1987.

20. Высшая математика. Сборник задач / под ред. Овчинникова П.Ф.. — К.: Вища школа, 1991.

21. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.1, Донецк. Норд-компьютер, 2002, 528с.

22. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.2, Донецк. Норд-компьютер, 2004, 458с.

1-10. Даны координаты вершин треугольника . Найти: 1) Длины сторон треугольника; 2) Внутренний угол при вершине A треугольника; 3) Уравнение прямой BC; 4) Уравнение высоты, опущенной из вершины A; 5) Уравнение прямой, проходящей через вершину A, параллельно стороне BC.

1. .

2. .

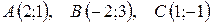3. .

4. .

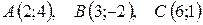5. .

6. .

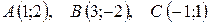7. .

8. .

9. .

10. .

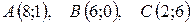Пример.

1) Найдем сначала координаты векторов , и . Для этого из координат конца вектора вычитаем координаты его начала:

.

.

.

Модуль вектора (равный расстоянию между точками A и B, A и C, B и C) представляет собой корень из суммы квадратов координат соответствующего вектора:

.

.

.

2) Внутренний угол при вершине A треугольника найдем как угол между сторонами AB и AC треугольника. Этот угол равен углу между векторами и 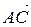и находится по формуле:

.

Тогда ; .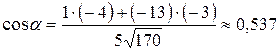

3) Уравнение прямой BC запишем используя уравнение прямой, проходящей через две точки с координатами и :

.

Подставляя значения координат точек B и C, получим

.

После приведения подобных получим уравнение прямой BC:

.

4) Высота, опущенная из вершины , перпендикулярна стороне . Следовательно скалярное произведение вектора, лежащего на высоте (будем обозначать его ) и вектора равно нулю. Вектор имеет координаты , где x и y – координаты произвольной точки, лежащей на высоте. Запишем скалярное произведение :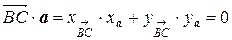

.

После раскрытия скобок и приведения подобных получим

;

.

Это и есть искомое уравнение высоты.

5) Вектор , параллельный стороне , имеет координаты , где x и y – координаты произвольной точки этого вектора. Из условия параллельности векторов и следует . Подставляя в это соотношение координаты соответствующих векторов и приводя подобные получим

; ;

; .

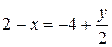11-20. Даны координаты вершин пирамиды A₁A₂A₃A₄. Найти: 1) длину ребра A₁A₂; 2) угол между ребрами A₁A₂ и A₁A₄; 3) площадь грани A₁A₂A₃; 4) объем пирамиды; 5) уравнение плоскости A₁A₂A₃; 6) уравнения прямой A₁A₄; 7) Угол между ребром A₁A₄ и гранью A₁A₂A₃; 8) уравнение высоты, опущенной из вершины A₄ на плоскость A₁A₂A₃.

11.

12.

13.

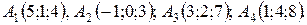
14.

15.

16.

17.

18.

19.

20.

Пример.

Если точка 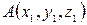- начало вектора, а точка - его конец, то координаты вектора находятся по формулам

1) Найдем сначала координаты вектора :

.

Модуль вектора (равный расстоянию между точками A₁ и A₂)представляет собой корень из суммы квадратов координат вектора:

.

2) Угол между ребрами A₁A₂ и A₁A₄ равен углу между соответствующими векторами и находится по формуле:

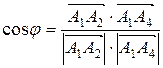, где - скалярное произведение векторов, записанное в координатной форме.

Координаты вектора 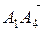равны:

, .

Тогда ; .

3) Уравнение плоскости, проходящей через три заданные точки , , 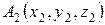, 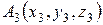имеет вид:

.

Подставляя значения координат, вычисляем определитель:

Итак, искомое уравнение плоскости имеет вид

или .

4) Уравнения прямой, проходящей через точки и , имеет вид

.

Таким образом, получаем искомые уравнения:

.

5) Если даны плоскость с нормальным вектором и прямая 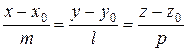с направляющим вектором , то угол между прямой и плоскостью определяется по формуле

.

Так как , а , то

, .

6) Площадь треугольника, построенного на двух векторах, равна половине модуля векторного произведения этих векторов:

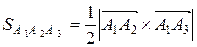, где - векторное произведение векторов. и .

Так как

,

то

(кв. ед.).

7) Объем пирамиды, построенной на трех векторах, равен одной шестой модуля смешанного произведения этих векторов:

.

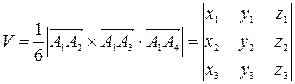Следовательно,

(куб. ед.)

8) Так как в качестве направляющего вектора прямой, проходящей через заданную точку D перпендикулярно плоскости ABC, можно выбрать вектор нормали n к плоскости, то канонические уравнения искомой прямой запишется в виде

.

Пример.2. Из точки P(2;3;-5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.

Основаниями перпендикуляров, опущенных из точки P(2;3;-5) на координатные плоскости, служат точки P₁(2;3;0), P₂(2;0;-5) и P₃(0;3;-5). требуется составить уравнение плоскости, проходящей через три заданные точки.

Чтобы найти нормальный вектор плоскости, рассмотрим два вектора и . Они лежат в искомой плоскости, значит, 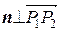и . Следовательно,

,

Уравнение искомой плоскости, проходящей через точку M₁(x₁, y₁, z₁) перпендикулярно вектору 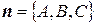, имеет вид :

;

.

в) Составить канонические уравнения прямой

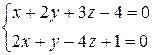
Чтобы найти какую – либо точку, принадлежащую прямой, зафиксируем одну переменную, например z, положив z = 0, и решим полученную систему двух уравнений с двумя неизвестными

Таким образом, одна из точек, принадлежащих прямой, имеет координаты .

Теперь найдем направляющий вектор прямой. Так как 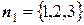и , то

.

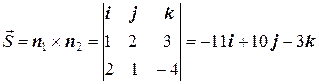Канонические уравнения прямой запишутся в виде:

.

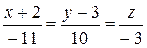Дата добавления: 2014-11-18