Ранг матрицы

Общая задача Л.П.

Л.П.- наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Пусть дана система m неравенств с n - неизвестными.

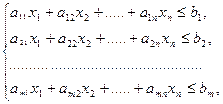(1)

х_1,2 0 должно быть всегда (по смыслу экономических задач).

- линейная функция.

Необходимо найти такое решение системы Х = (х₁,х₂,….,х_n), при котором линейная функция Z принимает оптимальное, т.е. мах(min) значение. Такую систему линейных неравенств называют системой ограничений, а функцию Z – целевой функцией (или линейной функцией, линейной формой, функцией цели).

В общем виде задачу можно записать так:

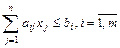
Оптимальным решением, или оптимальным планом задачи ЛП называют решение Х = (х₁,х₂,…х_n) системы ограничений, при котором линейная функция Z принимает оптимальное решение.

ü Если система ограничений состоит из одних неравенств, то задача называется стандартной;

ü если же из уравнений, то задача, называется канонической;

ü если из уравнений и неравенств, то неканонической или общей.

Чтобы перейти от стандартной формы к каноническому виду вводят дополнительные неотрицательные переменные со знаком «+», если знак неравенства «≤» и со знаком «-», если знак неравенства «≥», т.е. неравенство можно заменить выражением .

Решение экономической задачи можно разбить на три этапа:

1. построение экономико-математической модели;

2. нахождение оптимального решения;

3. практическое внедрение полученных результатов в народном хозяйстве.

Чтобы составить математическую модель задачи Л.П. необходимо:

a. ввести обозначения переменных;

b. исходя из цели экономических исследований, составить целевую функцию;

c. учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений.

Для рассмотрения решения задач Л.П. необходимо вспомнить некоторые понятия аналитической геометрии и линейной алгебры.

Рангом матрицы А называют наивысший порядок отличных от 0 миноров этой матрицы. Обозначается: r(A).

1. Если матрица имеет размерность (m х n), то её ранг не превосходит меньшего из её размеров: .

2. Если все элементы матрицы равны 0, то ранг матрицы равен 0:

3. Для квадратной матрицы n- го порядка ранг матрицы равен n, если определитель матрицы отличен от 0: ∆≠0, т.е. если матрица невырожденная.

В общем случае, определение ранга матрицы перебором всех миноров достаточно трудоемко, поэтому применяют элементарные преобразования, которые сохраняют ранг матрицы:

1. Отбрасывание нулевой строки или столбца.

2. Умножение всех элементов строки (столбца) на число, не равное 0.

3. Изменение порядка строк или столбцов.

4. Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое постоянное число.

5. Транспонирование матрицы.

§3. Системы m линейных уравнений с n переменными.

В задачах Л.П. интерес представляют системы, в которых ранг матрицы А меньше числа переменных, т.е. 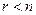или иначе, максимальное число независимых уравнений (неравенств) системы меньше числа переменных.

Пусть дана система 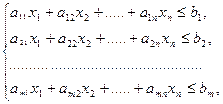(1):

(1)

Выпишем матрицу А:

Будем предполагать, что в данной системе все m неравенств (уравнений) независимы, т.е. r(A) = m, m<n.

· Любые m переменные этой системы называются основными или базисными, если определить матрицы коэффициентов при них отличен от 0, тогда как остальные (n-m) переменные называется свободными или неосновными.

Основными могут быть разные группы из n переменных и отличаться они будут друг от друга только самими элементами (переменными). Таких групп максимальное число может быть 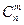, т.к. могут быть случаи, что ∆=0, то их число n ≤ .

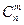Теорема. Если для системы m линейных уравнений с n переменными, где m ≤ n, ранг матрицы коэффициентов при переменных r = m, т.е. существует хотя бы одна группа базисных переменных, то эта система является неопределенной, причем каждому произвольному набору значений свободных переменных соответствует одно решение системы.

· Решение системы линейных уравнений Х = (х₁,х₂,….,х_n) называют опорным или допустимым, если оно содержит лишь неотрицательные компоненты, в противном случае решение называется недопустимым.

В задачах Л.П. именно такие решения представляют интерес.

· Решение системы m уравнений с n переменными называется базисным, если все (n - m) свободные переменные равны 0. В случае если m ≠ n систему можно решать методом Гаусса.

Если ранг системы равен n, то все m уравнений является линейно-независимыми, а остальные уравнения являются их линейной комбинацией.

1. Если r = n, то система имеет единственное решение.

2. Если r < n, то система имеет множество решений, которые определяются свободными переменными.

3. Если в порядке исключения неизвестных получается строка

о · х₁ + о · х₂ +….о · х_n = в_i, где в_i ≠ 0, то говорят, что система несовместна, т.е. решений не имеет.

Дата добавления: 2014-11-08