
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
А В – элементы Найти объединение, пересечение, разность и дизъюнктивную сумму множеств А и В
|
|
|
|
Решение: 1. Объединение (сумма) А 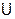 В есть множество всех элементов, принадлежащих А или В. Тогда
В есть множество всех элементов, принадлежащих А или В. Тогда 
2. Пересечение (произведение) 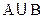 есть множество всех элементов принадлежащих одновременно как А, так и В. Тогда:
есть множество всех элементов принадлежащих одновременно как А, так и В. Тогда:  .
.
3. Разность А \ В есть множество, состоящее из всех элементов А, не входящих в В. Тогда: 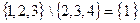 .
.
4. Дизъюнктивная сумма 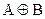 есть множество элементов, принадлежащих или А, или В (но не обоим вместе). Тогда
есть множество элементов, принадлежащих или А, или В (но не обоим вместе). Тогда  .
.
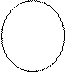
Задача 2. Дано  Требуется использовать круги Эйлера для наглядного изображения соотношений между подмножествами А и В, составляющих универсум
Требуется использовать круги Эйлера для наглядного изображения соотношений между подмножествами А и В, составляющих универсум  .
.
|
|
|
|












 1 2 3 4
1 2 3 4
 | |||||||
 | |||||||
 | |||||||
 | |||||||

Задача 3. Дано: число а, в, с n=3 различных элементов. Требуется найти число перестановок этих элементов.
Решение: 1. Качественный анализ показывает, что число перестановок без повторений а, в, с; в, а, с; в, с, а; а, с, в; с, в, а; с, а, в равно 6.
2. По формуле: 
Задача 4. Дано: число n = 3 элементов с повторениями: а, а, в двух типов: тип “а” повторяется 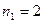 раза, тип “в” повторяется
раза, тип “в” повторяется 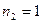 раз. Требуется найти число перестановок этих элементов.
раз. Требуется найти число перестановок этих элементов.
Решение: 1. Качественный анализ показывает, что число перестановок с повторениями а, а, в; а, в, а; в, а, а; равно 3.
2. По формуле:
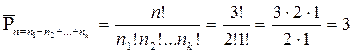
Задача 5. Дано число n =3 различных элементов: а, в, с. Требуется найти число размещений этих элементов по m = 2 без повторений.
Решение: 1. Качественный анализ показывает, что число размещений из n = 3 по m = 2 без повторений а, в; в, а; а, с; с, а; в, с; с, в равно 6.
2. По формуле:
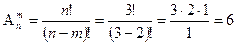
Задача 6. Дано:число m=3 элементов повторениями 2-х типов (k=2): тип «а» и тип «b».Требуется найти число размещений этих элементов по m=3.
|
|
|
Решение: 1. Качественный анализ показывает, что число размещений с повторениями из элементов двух типов (k=2) по m=3 элементов а, а, а; b, a, a; a, b, a; a, a, b; b, b, a; b, a, b; a, b, b; b, b, b равно 8.
2. По формуле:
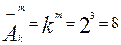
Задача 7. Дано число n=3 различных элементов: a, b, c. Требуется найти число сочетаний этих элементов по m=3.
Решение: 1. Качественный анализ показывает, что число сочетаний из n=3 элементов по m=2 a, b; a, c; c, b (сочетания отличаются друг от друга только составом элементов, т.е. a, b и b, a - это одно и тоже сочетание) равно 3.
2. По формуле:

Задача 8. Даночисло элементов двух типов k=2: тип “a” и тип “b”. Требуется найти число сочетаний этих элементов по m=3 элементов.
Решение: 1. Качественный анализ показывает, что число сочетаний их k=2 типов элементов по m=3 с повторениями a, a, a; b, a, a; b, b, a; b, b, b равно 4.
2. По формуле:

II. Векторная алгебра- это раздел математики, изучающий величины (векторы), которые характеризуются одновременно как числом (положительным, отрицательным, равным нулю), так и направлением в трехмерном (или двухмерном) пространстве.
Задача 9. Даны координаты вершин пирамиды АВСD: А (2;1;0), В (3;-1;2), С (13;3;10), D (0;1;4). Требуется: 1) записать векторы  в системе орт i, j, k и найти модули этих векторов; 2) найти угол между векторами
в системе орт i, j, k и найти модули этих векторов; 2) найти угол между векторами 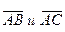 ; 3) найти проекцию вектора
; 3) найти проекцию вектора 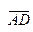 на вектор
на вектор 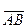 ; 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD.
; 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD.
Решение. 1. Произвольный вектор а может быть представлен в системе орт i, j, k следующей формулой:
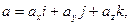 (1)
(1)
где ах, ау, аz – проекции вектора а на координатные оси Ох, Оу и Оz, а i, j, и k – единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Оz. Если даны точки М1 (х1;у1;z1) и М2 (х2;у2;z2), то проекции вектора 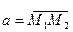 на координатные оси находятся по формулам:
на координатные оси находятся по формулам:
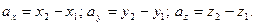 (2)
(2)
Тогда
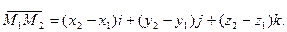 (3)
(3)
Подставив в (3) координаты точек А и В, получим вектор 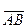 :
:
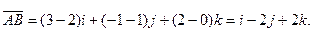
Аналогично, подставляя в (3) координаты точек А и С, находим
|
|
|

Подставив в (3) координаты точек А и D, находим вектор 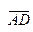 :
:
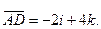
Если вектор а задан формулой (1), то его модуль вычисляется по формуле
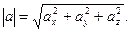 (4)
(4)
Применяя (4), получим модули найденных векторов:

2. Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей. Находим скалярное произведение векторов 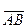 и
и  :
:

Модули этих векторов уже найдены: 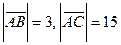 . Следовательно,
. Следовательно,

3. Проекция вектора 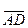 на вектор
на вектор 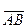 равна скалярному произведению этих векторов, деленному на модуль вектора
равна скалярному произведению этих векторов, деленному на модуль вектора 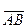 :
:

Площадь грани АВС равна половине площади параллелограмма, построенного на векторах 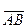 и
и  . Обозначим векторное произведение вектора
. Обозначим векторное произведение вектора 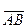 на вектор
на вектор  через вектор Р. Тогда, как известно, модуль вектора Р выражает собой площадь параллелограмма, построенного на векторах
через вектор Р. Тогда, как известно, модуль вектора Р выражает собой площадь параллелограмма, построенного на векторах 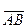 и
и  , площадь грани АВС будет равна половине модуля вектора Р:
, площадь грани АВС будет равна половине модуля вектора Р:
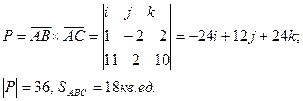
5. Объем параллелепипеда, построенного на трех некомпланарных вектора, равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение 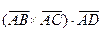 :
:

Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды АВСD равен 24 куб. ед.
Матрицы – это раздел дискретной математики, изучающий совокупности чисел или объектов другой природы, расположенных в виде прямоугольной таблицы.
Задача 10. Дана сислема линейных уравнений:
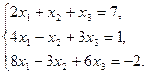 (1)
(1)
Требуется: 1).записать исходную систему линейных уравнений в матричной форме; 2). решить систему линейных уравнений с помощью обратной матрицы.
Решение. 1. Пусть А – матрица коэффициентов при неизвестных; Х – матрица-столбец неизвестных х1, х2, х3 и Н – матрица-столбец из свободных членов:

Левую часть системы (1) можно представить в виде произведения матриц А.Х, а правую – в виде матрицы Н. Следовательно, имеем матричное уравнение
А.Х=Н. (2)
Если определитель матрицы А отличен от нуля, то матрица А имеет обратную матрицу А-1. В этом случае можно обе части равенства (2) умножить слева на матрицу А-1, получим
А-1.А.Х=А-1.Н.
Так как А-1.А=Е, где Е – единичная матрица, а Е.Н=Х, то матричная запись решения системы линейных уравнений будет иметь вид
Х= А-1.Н. (3)
2. для нахождения обратной матрицы А-1 необходимо сначала найти определитель

|
|
|
Тогда обратная матрица  определяется путем последовательности трех шагов:
определяется путем последовательности трех шагов:
1). элементы матрицы А заменяются их алгебраическими дополнениями 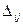 , т.е. определителями, полученными удалением из матрицы А S-й строки и K-го столбца, причём каждый определитель умножается еще на (-1)s+k:
, т.е. определителями, полученными удалением из матрицы А S-й строки и K-го столбца, причём каждый определитель умножается еще на (-1)s+k:
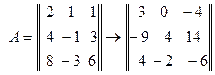
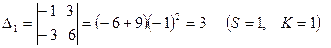


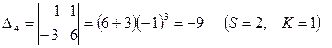



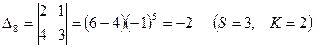
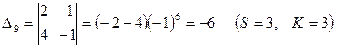
2). матрица алгебраических дополнений транспонируется, в результате чего получают взаимную (присоединенную) матрицу а А (Аdj A)

3). взаимная матрица умножаемая на det A и получаются

3. В соответствии с (3) можно записать
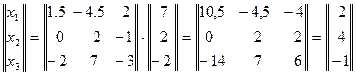
Следовательно, решение системы линейных уравнений х1= 2, х2 = 4, х3 = -1.
Задача 11. Дана система линейныхравнений:
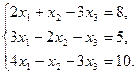
Требуется: 1). определить совместна ли исходная система линейных уравнений; 2). решить систему, если она совместна.
Решение. 1. Определение расширенной матрицы путем присоединения к матрице А (матрица, составленная из коэффициентов при неизвестных х1, х2, х3).
 столбца свободных членов
столбца свободных членов 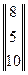
Тогда получают расширенную матрицу системы:

2. Определение рангов матриц А и В
2.1. Преобразование матрицы А по правилу: сумму элементов первых двух столбцов прибавим к соответствующим элементам третьего столбца:
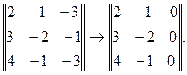
Анализ показывает, что определитель третьего порядка 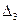 равен нулю, т.к. все элементы третьего столбца равны нулю. Определитель второго порядка
равен нулю, т.к. все элементы третьего столбца равны нулю. Определитель второго порядка 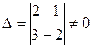 . Следовательно, ранг матрицы А равен 2, т.е. r(A) =2.
. Следовательно, ранг матрицы А равен 2, т.е. r(A) =2.
2.2. Первое преобразование матрицы В по правилу: сумму элементов первых двух столбцов прибавим к соответствующим элементам третьего столбца.
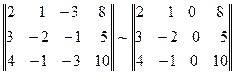
Тогда все элементы третьего столбца равны нулю.
Вторые преобразования матрицы В по правилу: элементы первого столбца умножить –3, второго на –2 и их сумму вычесть из соответствующих элементов четвертого столбца:
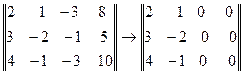
Так как элементы двух последних столбцов равны нулю, то все определители третьего порядка матрицы В раны нулю и, следовательно, ранг матрицы В равен 2, т.е. r(В) =2.
Вывод: система линейных уравнений совместна, т.к. выполнено необходимое и достаточное условие r(A) = r(В) =2.
3. Поскольку ранг матриц А и В равны 2, а система содержит 3 неизвестных, то она имеет бесконечное число решений. Пусть выбран базисный определитель 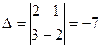 , а в качестве базисных неизвестных х1 и х2. Составляем подсистему, состоящую из первых двух уравнений заданной системы и свободное неизвестное х3 переносим в правую часть. Получаем
, а в качестве базисных неизвестных х1 и х2. Составляем подсистему, состоящую из первых двух уравнений заданной системы и свободное неизвестное х3 переносим в правую часть. Получаем
|
|
|
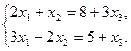
4. Решая последнюю систему относительно базисных неизвестных х1 и х2, находим х1=3+х3, х2=2+х3. Полученное решение называется общим. Конкретные решения получают задавшись х3. Например, пусть х3 =-2, тогда х1 =1, х2 =0.
IV. Функциональный анализ – это раздел математики, изучающий свойства операторов, действующих между любыми (главным образом функциональными) пространствами. Основными понятиями функционального анализа являются: предел, функция, производная.
Задача 12. Найти пределы этих выражений:
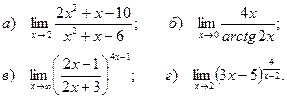
Решение. 1. Непосредственная подстановка предельного значения аргумента х =2 приводит к неопределенности вида 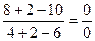 .
.
Для раскрытия неопределенности необходимо:
- разложим числитель и знаменатель дроби на множители
 и
и 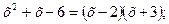
- сократить дробь на общий множитель (х-2).
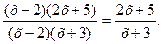
Тогда

б) пусть arctg 2x=y. Тогда 2х=tg y; очевидно, что если х®0, то y®0.
Следовательно,

Используя первый замечательный предел, можно осуществить следующее преобразование:
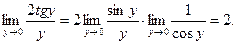
Существует второй способ нахождения предела на основе того, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной. Так как при х®0 arctg 2x~2х, то
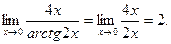
3. При х®¥ основание  стремиться к 1, а показатель степени 4х+1 стремиться к бесконечности. Следовательно, имеем неопределенность вида 1 ¥. Для раскрытия неопределенности следует представить основание в виде суммы 1 и некоторой бесконечно малой величины:
стремиться к 1, а показатель степени 4х+1 стремиться к бесконечности. Следовательно, имеем неопределенность вида 1 ¥. Для раскрытия неопределенности следует представить основание в виде суммы 1 и некоторой бесконечно малой величины:
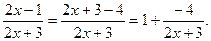
Тогда

Положим 2х+3=-4у; следовательно при х®+¥ переменная у® -¥. Выразим показатель степени через новую переменную у. Так как 2х=-4у-3, то 4х+1=-8у-5.
Таким образом,
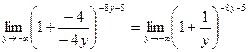
Используя второй замечательный предел, можно осуществить следующее преобразование:

(используем второй замечательный предел).
4. При х®2 основание (3х-5) стремится к единице, а показатель степени  стремиться к бесконечности.
стремиться к бесконечности.
Пусть 3х-5=1+a, где a®0 при х®2. Тогда:

Выразив основание и показатель степени через a, получим

----------------------------------------------------------------------------------------

Задача 13. Дана функция у задана различными аналитическими выражениями для различных областей изменения аргумента х:

Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти предел функции у при приближении аргумента х к точке разрыва слева и справа; 3) найти скачок функции в точке разрыва. 4). построить график данной функции y = f(x).
Решение. 1. Данная функция определена и непрерывна в интервалах (- ¥, -2), (-2, 1) и (1, + ¥). При х =-2 и х =1 меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.
2. Односторонние пределы в функции в точке х =-2:
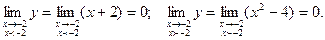
Односторонние пределы совпадают. Функция в этой точке непрерывна.
3. Односторонние пределы функции в точке х =1 равны:
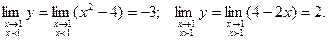
Односторонние пределы функции у в точке х =1 не равны между собой, то в этой точке функция имеет разрыв первого рода.
4. Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельным значениями. Следовательно, в точке х =1 скачок функции  .
.
5. График функции y = f(x)
 |
-2
-4
Задача 14. Дана функция  и значение аргумента х1 = -2 и х2 = 3
и значение аргумента х1 = -2 и х2 = 3
Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва;
3) построить график данной функции на отрезке [-6;6].
Решение. Если ищется предел функции у=f(х) при условии, что аргумент х, стремясь к своему предельному значению a, может принимать только такие значения, которые меньше a, то этот предел, если он существует, называется правосторонним (правым) пределом данной функции в точке х=a и условно обозначается так:
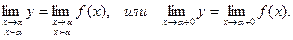
Функция у=f(х) непрерывна при х=a, если выполняются следующие условия: 1) функция у=f(х) определена не только в точке a, но и в некотором интервале, содержащем эту точку;
2) функция у=f(х) имеет при х®a конечные и равные между собой односторонние пределы;
3) односторонние пределы при х®a совпадают со значением функции в точке a, т.е.
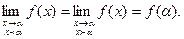
Если для данной функции у=f(х) в данной точке х=a хотя бы одно из перечисленных трех условий не выполняется, то функция называется разрывной в точке х=a.
Разрыв функции у=f(х) в точке х=a называется разрывом первого рода, если односторонние пределы слева и справа существуют, но не равны между собой. Если же хотя бы один из односторонних пределов не существует, разрыв в этой точке называется разрывом второго рода.
2. При х1 = -2 данная функция  не существует: в этой точке функция терпит разрыв.
не существует: в этой точке функция терпит разрыв.
3. Односторонние пределы функции при х1 ® -2 слева и справа

так как знаменатель стремится к нулю, оставаясь отрицательным;
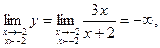
так как знаменатель стремится к нулю, оставаясь положительным.
Следовательно, при х = -2 данная функция имеет разрыв второго рода.
4. При х =3 данная функция  т.е. она в этой точке непрерывна, так как выполняются все три условия непрерывности функции.
т.е. она в этой точке непрерывна, так как выполняются все три условия непрерывности функции.
5. График функции имеет вид:
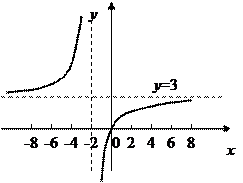 |
Задача 15. Даны три функции вида:
1) 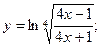 2)
2) 
3)  4)
4) 
Требуется найти производные 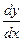 функций
функций
Решение. 1. Пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:
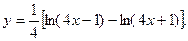
Применяя правила и формулы дифференцирования, получают:

2. Осуществляют логарифмирование по основанию обеих частей равенства:
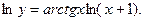
Теперь дифференцируют обе части равенства, считая ln у сложной функцией от переменной х:
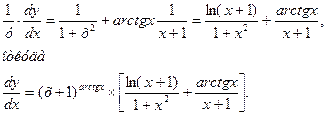
3. В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную 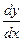 , необходимо дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной
, необходимо дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной 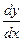
Дифференцируя обе части исходного уравнения, находят:

Из полученного равенства, связывающего х, у и 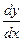 , находим производную путем преобразований:
, находим производную путем преобразований:
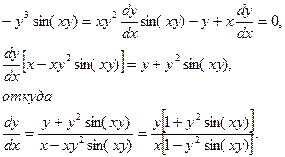
4. Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную, необходимо предварительно найти дифференциалы dx и dy и затем взять их отношение:
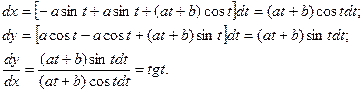
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1349; Нарушение авторских прав?; Мы поможем в написании вашей работы!