Сходимость монотонной последовательности

Монотонные последовательности

Пример.

Решение.

Примеры.

3.21. Доказать, что для произвольного .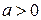

1) Пусть . Тогда 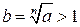, т.к. в противном случае и при перемножая это неравенство n раз получим , что противоречит условию .

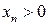Положим , тогда и 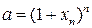. Применим неравенство Бернулли:

,

то есть 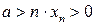. Тогда, так как 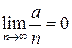, учитывая теорему 3.6, получаем

,

и, значит, . Из теоремы 3.8 следует, что .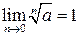

2) Пусть 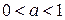. Обозначим 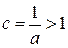. По доказанному для 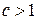выполнено . Тогда

.

3) Пусть 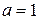, тогда 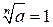и, следовательно, .

3.22. Доказать, что 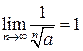для произвольного .

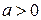Решение. Воспользуемся примером 3.26:

.

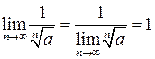3.23. Вычислить .

Решение. Воспользуемся очевидным неравенством:

.

Следовательно,

.

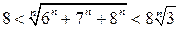Так как (см. пример 3.21), то и по теореме 3.6 получаем, что

.

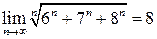ТЕОРЕМА 3.9. Если 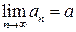, , , 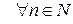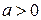то .

ТЕОРЕМА 3.10. Если 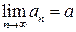, , 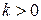то .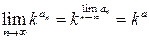

3.24. Вычислить предел .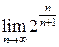

Решение. Используя свойство VII, получаем .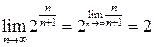

ТЕОРЕМА 3.11. Если 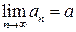, , , , 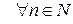, 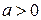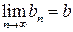то .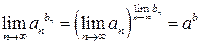

Определение 3.11. Последовательность 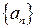называется возрастающей (строговозрастающей), если выполняется неравенство ().

Определение 3.12. Последовательность 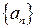называется убывающей (строгоубывающей), если выполняется неравенство ().

Определение 3.13. Возрастающие и убывающие последовательности называются монотонными.

Например, последовательность 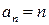строго возрастает, последовательность строго убывает, а последовательность не является монотонной

ТЕОРЕМА 3.12 (о пределе возрастающей последовательности). Всякая возрастающая, ограниченная сверху последовательность имеет предел.

Доказать самостоятельно.

Замечание 3.6. Можно доказать что всякая возрастающая неограниченная сверху последовательность 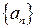стремится к .

Действительно, так как 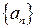не ограничена сверху, то 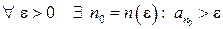. Тогда в силу возрастания: , то есть .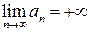

ТЕОРЕМА 3.13 (о пределе убывающей последовательности). Всякая убывающая ограниченная снизу последовательность имеет предел.

Доказать самостоятельно.

Дата добавления: 2014-12-08