
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Мультиколінеарність
Наявність лінійного функціонального або тісного кореляційного зв’язку між двома чи декількома пояснювальними змінними називають мультиколінеарністю. У першому випадку мультиколінеарність проявляється у явній (функціональній) формі, а у другому – у стохастичній формі.
Якщо має місце функціональна форма мультиколінеарності, то один із стовпців матриці 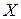 є лінійною комбінацією інших стовпців, а отже і матриця
є лінійною комбінацією інших стовпців, а отже і матриця 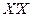 є виродженою (її визначник дорівнює нулю). Тому не можна знайти розв’язок системи нормальних рівнянь і 1МНК не забезпечує отримання оцінок параметрів рівняння регресії.
є виродженою (її визначник дорівнює нулю). Тому не можна знайти розв’язок системи нормальних рівнянь і 1МНК не забезпечує отримання оцінок параметрів рівняння регресії.
Найчастіше у практичних дослідженнях мультиколінеарність зустрічається у стохастичній формі. У такому випадку матриця 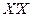 не є виродженою, але її визначник є близьким до нуля. Хоча теоретично можна оцінити значення параметрів рівняння регресії, елементи вектора оцінок В і його дисперсійно-коваріаційної матриці будуть обернено пропорціональними до визначника
не є виродженою, але її визначник є близьким до нуля. Хоча теоретично можна оцінити значення параметрів рівняння регресії, елементи вектора оцінок В і його дисперсійно-коваріаційної матриці будуть обернено пропорціональними до визначника 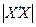 . Як наслідок, великими виявляться стандартні похибки (середні квадратичні відхилення) коефіцієнтів регресії. Не зважаючи на те, що модель може виявитися адекватною за
. Як наслідок, великими виявляться стандартні похибки (середні квадратичні відхилення) коефіцієнтів регресії. Не зважаючи на те, що модель може виявитися адекватною за  -критерієм, оцінка значущості параметрів
-критерієм, оцінка значущості параметрів 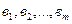 дасть негативні практичні результати.
дасть негативні практичні результати.
У практиці економічних досліджень явище мультиколінеарності є досить поширеним і виникає у зв’язку з такими причинами:
• має місце тенденція одночасної зміни декількох факторів (наявність трендів у факторних рядах динаміки);
• до моделі включено лагові змінні;
• використання в якості інформаційної бази моделі малої скінченої сукупності спостережень.
Оцінювання параметрів моделі при наявності у масиві пояснювальних змінних мультиколінеарності за допомогою 1МНК пов’язано з такими наслідками:
• велика дисперсія і коваріація оцінок параметрів моделі;
• збільшуються похибки оцінок параметрів моделі, а отже і відповідно інтервалів довіри;
• статистична незначущість оцінок параметрів моделі.
Існує декілька кількісних критеріїв для визначення наявності або відсутності мультиколінеарності. Найпростішим з них є підхід, який базується на аналізі матриці коефіцієнтів парної кореляції між пояснювальними змінними 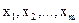 :
:
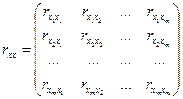 .
.
Якщо серед елементів матриці 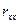 є такі, значення яких перевищує 0,8, то між відповідними змінними існує мультиколінеарність. Проте потрібно відзначити, що мультиколінеарність не зводиться лише до існування парної кореляції між двома незалежними змінними. У випадку більше, ніж двофакторної регресійної моделі, мультиколінеарність може існувати навіть при відносно невеликих значеннях парних коефіцієнтів кореляції. Тому більш загальна перевірка наявності мультиколінеарності передбачає знаходження множинного коефіцієнта детермінації між однією із незалежних змінних і деякою групою незалежних змінних. Наявність високого значення такого множинного коефіцієнта детермінації (як правило, більшого за 0,6) вказує на мультиколінеарність у масиві незалежних змінних.
є такі, значення яких перевищує 0,8, то між відповідними змінними існує мультиколінеарність. Проте потрібно відзначити, що мультиколінеарність не зводиться лише до існування парної кореляції між двома незалежними змінними. У випадку більше, ніж двофакторної регресійної моделі, мультиколінеарність може існувати навіть при відносно невеликих значеннях парних коефіцієнтів кореляції. Тому більш загальна перевірка наявності мультиколінеарності передбачає знаходження множинного коефіцієнта детермінації між однією із незалежних змінних і деякою групою незалежних змінних. Наявність високого значення такого множинного коефіцієнта детермінації (як правило, більшого за 0,6) вказує на мультиколінеарність у масиві незалежних змінних.
Найчастіше у практиці економетричних досліджень, які стосуються виявлення мультиколінеарності, користуються методом Феррара-Глобера. Повна реалізація методу передбачає використання трьох критеріїв:
• 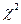 -критерію (хі- квадрат) - для перевірки наявності мультиколінеарності в масиві незалежних змінних;
-критерію (хі- квадрат) - для перевірки наявності мультиколінеарності в масиві незалежних змінних;
•  -критерію – для перевірки мультиколінеарності кожної незалежної змінної зі всіма іншими;
-критерію – для перевірки мультиколінеарності кожної незалежної змінної зі всіма іншими;
• 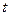 -критерію– для перевірки мультиколінеарності кожної пари змінних.
-критерію– для перевірки мультиколінеарності кожної пари змінних.
Реалізація алгоритму Феррара-Глобера полягає у виконанні таких процедур:
1. Стандартизація (нормалізація) пояснювальних змінних за допомогою одного із методів:
а)  ;
;  (4.63)
(4.63)
б)  , (4.64)
, (4.64)
де 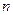 - кількість спостережень;
- кількість спостережень;
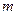 - кількість пояснювальних змінних;
- кількість пояснювальних змінних;
 - середнє значення
- середнє значення 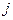 -ої змінної;
-ої змінної;
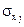 - середнє квадратичне відхилення
- середнє квадратичне відхилення 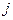 -ої змінної.
-ої змінної.
2. Знаходження кореляційної матриці згідно вибраного методу нормалізації::
а)  ; (4.65)
; (4.65)
б) 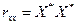 , (4.66)
, (4.66)
де  - матриця стандартизованих пояснювальних змінних;
- матриця стандартизованих пояснювальних змінних;
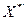 - матриця, транспонована до
- матриця, транспонована до  .
.
3. Розрахунок  -критерію:
-критерію:
 , (4.67)
, (4.67)
де  - визначник кореляційної матриці
- визначник кореляційної матриці 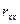 .
.
Для вибраного рівня значущості 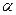 і
і  ступенів вільності з таблиць розподілу хі-квадрат знаходять критичне значення
ступенів вільності з таблиць розподілу хі-квадрат знаходять критичне значення  . Якщо
. Якщо  , то слід прийняти гіпотезу про те, що в масиві незалежних змінних існує мультиколінеарність.
, то слід прийняти гіпотезу про те, що в масиві незалежних змінних існує мультиколінеарність.
4. Якщо у масиві незалежних змінних виявлена мультиколінеарність, то переходять до перевірки існування мультиколінеарності між 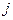 -ою та іншими пояснювальними змінними.
-ою та іншими пояснювальними змінними.
З цією метою розраховують послідовність  -критеріїв:
-критеріїв:
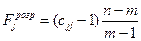 ,
,  (4.68)
(4.68)
де 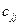 - діагональні елементи оберненої матриці
- діагональні елементи оберненої матриці 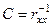 .
.
З таблиць  -розподілу для вибраного рівня значущості
-розподілу для вибраного рівня значущості 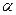 і
і  та
та 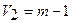 ступенів вільності знаходять критичне значення
ступенів вільності знаходять критичне значення 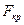 і порівнюють з розрахунковими. Якщо
і порівнюють з розрахунковими. Якщо 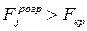 , то
, то 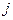 -та змінна мультиколінеарна з іншими незалежними змінними.
-та змінна мультиколінеарна з іншими незалежними змінними.
5. Перевірка парної мультиколінеарності 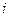 -ої незалежної змінної з
-ої незалежної змінної з 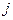 -ою, яка ґрунтується на обчисленні розрахункових значень
-ою, яка ґрунтується на обчисленні розрахункових значень 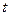 -критеріїв згідно формули:
-критеріїв згідно формули:
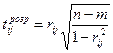 ,
, 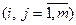 (4.69)
(4.69)
де  - частинні коефіцієнти кореляції.
- частинні коефіцієнти кореляції.
Частинні коефіцієнти кореляції дорівнюють:
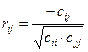 ,
, 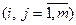 (4.70)
(4.70)
Розрахункові значення 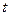 -критеріїв порівнюють з критичними
-критеріїв порівнюють з критичними  , знайденими для вибраного рівня значущості
, знайденими для вибраного рівня значущості 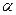 і
і  ступені вільності. Якщо
ступені вільності. Якщо  , то між змінними
, то між змінними 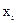 і
і 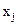 існує мультиколінеарність.
існує мультиколінеарність.
Приклад 4.2. На основі даних, поданих у табл.4.4, дослідити, чи існує у масиві спостережень мультиколінеарність.
Таблиця 4.4
Обсяг виконаних будівельно-монтажних робіт за одиницю часу, тис.грн.,
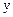
| Витрати на оплату праці, тис.грн.,
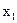
| Витрати на сировину і матеріали, тис.грн.,

| Транспортно-заготівельні витрати, тис.грн.,
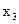
|
| 10,53 | |||
| 15,42 | |||
| 12,98 | |||
| 9,63 | |||
| 23,71 | |||
| 12,53 | |||
| 17,44 | |||
| 14,41 | |||
| 14,99 | |||
| 8,53 | |||
| 9,47 | |||
| 12,03 | |||
| 15,01 | |||
| 14,62 | |||
| 10,02 | |||
| 12,33 | |||
| 9,87 | |||
| 8,94 | |||
| 11,23 | |||
| 11,67 |
Для тестування наявності мультиколінеарності скористаємося методом Феррара-Глобера.
Спочатку обчислимо середні значення змінних, дисперсії, середні квадратичні відхилення:
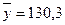 ;
; 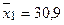 ;
;  ;
; 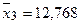 ;
;
 ;
;  ;
;  ;
; 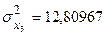 ;
;
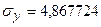 ;
;  ;
; 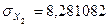 ;
; 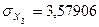 .
.
Далі проводимо нормалізацію змінних (користуємося формулою (4.64)).
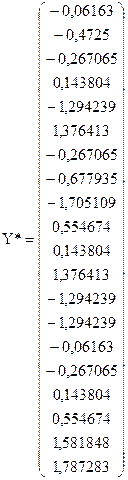
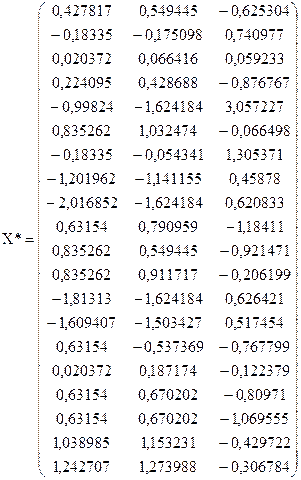
Згідно (4.66) знаходимо кореляційну матрицю, елементами якої є парні коефіцієнти кореляції між пояснювальними змінними:
 .
.
Детермінант матриці 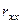 рівний:
рівний:
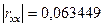 .
.
Обчислюємо розрахункове значення критерію хі-квадрат:
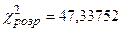 .
.
Для вибраного рівня значущості  і
і 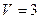 ступенів вільності з таблиць розподілу хі-квадрат отримуємо
ступенів вільності з таблиць розподілу хі-квадрат отримуємо 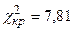 .
.
Так як має місце 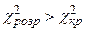 , то приходимо до висновку, що в масиві незалежних змінних існує мультиколінеарність.
, то приходимо до висновку, що в масиві незалежних змінних існує мультиколінеарність.
Продовжуючи реалізацію алгоритму Феррара-Глобера, знаходимо:
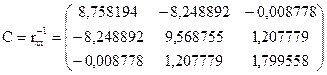 .
.
Визначаємо розрахункові значення  -критеріїв:
-критеріїв:
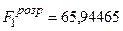 ;
;
 ;
;
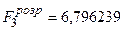 .
.
Для  і
і  та
та  з таблиць розподілу Фішера маємо
з таблиць розподілу Фішера маємо  .
.
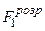 і
і  перевищують критичне значення, тому слід зробити висновок, що змінні
перевищують критичне значення, тому слід зробити висновок, що змінні 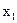 і
і  зумовлюють явище мультиколінеарності.
зумовлюють явище мультиколінеарності.
Розраховуємо частинні коефіцієнти кореляції, які характеризують зв'язок між двома змінними за умови, що інші змінні на цей зв'язок впливу не мають:
 ;
; 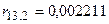 ;
; 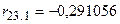 .
.
Коефіцієнт  є достатньо високим і вказує на наявність щільного зв’язку між змінними
є достатньо високим і вказує на наявність щільного зв’язку між змінними 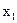 і
і  .
.
З метою тестування мультиколінеарності між змінними обчислюємо 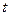 -критерії:
-критерії:
 ;
;  ;
; 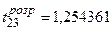 .
.
Для  і
і  ступенів вільності
ступенів вільності 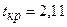 . Так як
. Так як 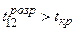 , то треба прийняти гіпотезу про мультиколінеарність між змінними
, то треба прийняти гіпотезу про мультиколінеарність між змінними 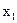 і
і  , тобто між витратами на оплату праці та витратами на сировину і матеріали.
, тобто між витратами на оплату праці та витратами на сировину і матеріали.
Використання 1МНК для масиву мультиколінеарних незалежних змінних може призвести до негативних наслідків, про які відзначалося вище. Однозначних засобів усунення негативного ефекту мультиколінеарності нема. Разом з тим, враховуючи ступінь мультиколінеарності та особливості досліджуваного явища, запропоновано декілька достатньо простих підходів, які дозволяють позбутися мультиколінеарності.
У випадку, коли має місце сильна мультиколінеарність, з моделі рекомендують вилучати одну із двох пов’язаних між собою пояснювальних змінних. Очевидно, що такий підхід є найпростішим, але слід звернути увагу на той факт, що вилучення з моделі змінної часто суперечить логіці зв’язків між економічними показниками і призводить до помилки специфікації моделі (некоректного визначення моделі). Тому, з однієї сторони, може бути досягнута мета ліквідації або пониження мультиколінеарності, а, з другої, - знайдені оцінки моделі можуть виявитися зміщеними, наслідки чого часто є гіршими, ніж сама проблема мультиколінеарності.
Інший підхід до пониження мультиколінеарності – збільшення кількості спостережень. На жаль, його практична реалізація не завжди можлива.
Для вилучення мультиколінеарності або послаблення її негативного ефекту застосовуються методи перетворення пояснювальних змінних:
• використання відносних значень змінних (темпи зростання, темпи приросту);
• використання відхилень від середніх значень змінних;
• нормалізація змінних.
З метою пониження негативного ефекту мультиколінеарності використовують також метод гребеневої регресії (“рідж-регресії”), суть якого полягає в посиленні обумовленості матриці нормальних рівнянь. При цьому оцінки параметрів рівняння регресії знаходять за допомогою оператора:
 , (4.71)
, (4.71)
де 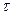 - додатне число;
- додатне число;
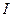 - одинична матриця.
- одинична матриця.
Однозначних рекомендацій щодо вибору 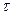 нема, а на практиці використовують значення
нема, а на практиці використовують значення 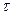 в діапазоні від 0,1 до 0,4.
в діапазоні від 0,1 до 0,4.
Визначник матриці  буде відмінним від нуля, але отримані оцінки будуть зміщеними. Разом з тим, доведено, що у випадку мультиколінеарності знайдеться таке значення
буде відмінним від нуля, але отримані оцінки будуть зміщеними. Разом з тим, доведено, що у випадку мультиколінеарності знайдеться таке значення 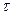 , для якого зміщена оцінка
, для якого зміщена оцінка  буде точнішою з точки зору середнього квадрата похибки
буде точнішою з точки зору середнього квадрата похибки  , ніж найкраща серед незміщених оцінок.
, ніж найкраща серед незміщених оцінок.
Користуючись методом гребеневої регресії, оцінимо параметри моделі на основі даних, поданих у табл.4.4.
Вхідні дані для моделювання представимо у вигляді відхилень індивідуальних значень від середніх:

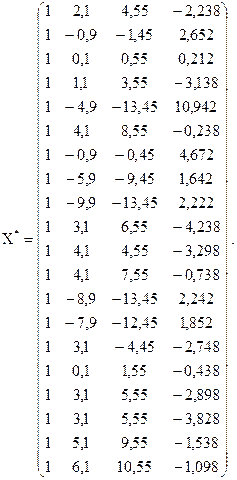
Тоді матриця  і обернена до неї
і обернена до неї 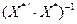 відповідно мають вигляд:
відповідно мають вигляд:
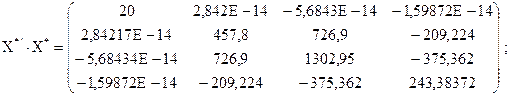
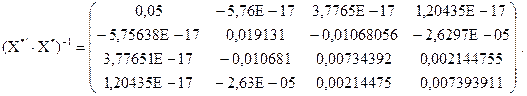
Використовуючи оператор оцінювання параметрів рівняння множинної лінійної регресії (4.25), знаходимо вектор оцінок:

Таким чином, якщо застосувати 1МНК, то отримаємо таке рівняння регресії:
 .
.
Тестування коефіцієнтів при змінних 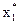 та
та  вказує на їх статистичну незначущість (нагадаємо, що у масиві змінних має місце мільтиколінеарність), а сума квадратів залишків рівна 59,409.
вказує на їх статистичну незначущість (нагадаємо, що у масиві змінних має місце мільтиколінеарність), а сума квадратів залишків рівна 59,409.
До діагональних елементів матриці  додамо гребінь
додамо гребінь 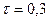 :
:


У цьому випадку вектор оцінок параметрів моделі лінійної множинної регресії рівний:
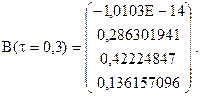
Порівнюючи значення оцінок 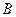 і
і 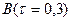 , бачимо, що вони суттєво не змінюються, а сума квадратів залишків залишилася рівною 59,409. Отже, можна зробити висновок, що серед зміщених оцінок параметрів ми знаходимо такі, які не є гіршими за незміщені.
, бачимо, що вони суттєво не змінюються, а сума квадратів залишків залишилася рівною 59,409. Отже, можна зробити висновок, що серед зміщених оцінок параметрів ми знаходимо такі, які не є гіршими за незміщені.
Для 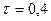 і
і 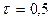 отримуємо такі оцінки:
отримуємо такі оцінки:
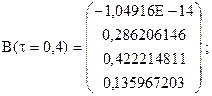
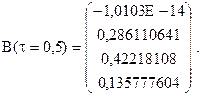
Якщо перераховані вище методи не забезпечують усунення мультиколінеарності, то в процесі побудови моделей множинної лінійної регресії можна скористатися методами пониження ознакового простору, які дають можливість виключити з моделі взаємозв’язані і незначущі фактори. Прикладом слугує метод головних компонент, який має декілька модифікацій.
|
|
Дата добавления: 2014-12-16; Просмотров: 7374; Нарушение авторских прав?; Мы поможем в написании вашей работы!