
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная алгебра
|
|
|
|
Прямоугольной 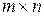 матрицей называется таблица чисел
матрицей называется таблица чисел
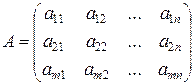 ,
,
содержащая m строк и n столбцов.
Числа 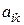 называются элементами матрицы. Первый индекс i указывает номер строки, в которой расположен элемент, а второй индекс k – номер столбца.
называются элементами матрицы. Первый индекс i указывает номер строки, в которой расположен элемент, а второй индекс k – номер столбца.
Матрица A называется квадратной матрицей n-го порядка, если m = n.
Квадратная матрица порядка n называется диагональной, если  при
при 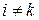 . Она выглядит следующим образом:
. Она выглядит следующим образом:
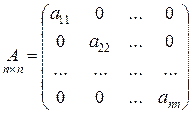 .
.
Элементы матрицы, для которых i = k, называются диагональными и образуют главную диагональ.
Диагональная матрица порядка п называется единичной матрицей, если все ее диагональные элементы равны единице 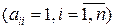 :
:
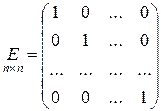 .
.
Суммой m ´ n матриц 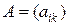 и B = (
и B = (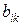 ) называется m ´ n матрица
) называется m ´ n матрица 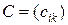 с элементами
с элементами
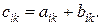 (1.1)
(1.1)
Произведением m ´ n матрицы A на число  называется m ´ n матрица В, для которой
называется m ´ n матрица В, для которой 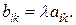
Произведением m ´ n матрицы 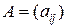 на
на 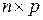 матрицу
матрицу 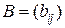 называется
называется 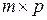 матрица С, элементы
матрица С, элементы 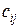 которой вычисляются согласно следующему правилу: каждый элемент
которой вычисляются согласно следующему правилу: каждый элемент 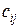 равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В:
равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В:
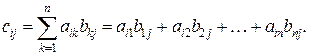 (1.2)
(1.2)
При решении многих математических задач возникает необходимость в сопоставлении квадратной матрице некоторого числа, называемого определителем. Рассмотрим квадратную матрицу второго порядка
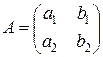 .
.
Определителем (детерминантом) второго порядка матрицы А называется число
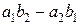 .
.
Определитель обозначается следующим образом:
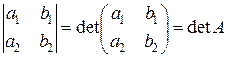 =
= 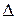 .
.
Для квадратной матрицы третьего порядка определитель вычисляется по формуле
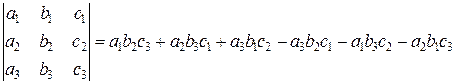 ,
,
 |
|
Пример. Вычислить определитель по правилу треугольников
 . v
. v
Минором 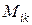 элемента
элемента 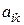 определителя n -го порядка
определителя n -го порядка 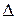 называется определитель (n – 1)-го порядка, который получается из
называется определитель (n – 1)-го порядка, который получается из 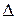 вычеркиванием i -й строки и k- го столбца.
вычеркиванием i -й строки и k- го столбца.
|
|
|
Алгебраическим дополнением 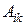 элемента
элемента 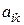 называется его минор
называется его минор 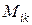 , умноженный на
, умноженный на 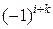 :
:
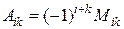 .
.
Нетрудно видеть, что знаки, которые следует ставить перед соответствующими минорами при вычислении алгебраических дополнений, чередуются в шахматном порядке.
Для вычисления определителей второго и третьего порядков существуют простые правила. Приведем теорему, облегчающую процедуру вычисления определителей более высоких порядков.
Теорема Лапласа. Определитель равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения
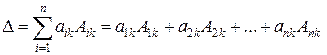
(разложение по элементам k -го столбца),
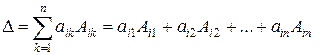
(разложение по элементам i -й строки). p
Пример. Вычислить определитель разложением по элементам первой строки
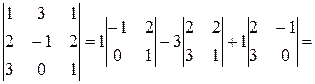
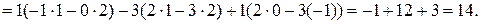 v
v
С помощью определителей удобно записывать решение систем линейных уравнений.
Рассмотрим систему трех линейных уравнений с тремя неизвестными
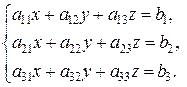
Обозначим через 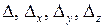 определитель системы D и вспомогательные определители, полученные из D заменой столбца коэффициентов при соответствующей неизвестной столбцом свободных членов:
определитель системы D и вспомогательные определители, полученные из D заменой столбца коэффициентов при соответствующей неизвестной столбцом свободных членов:
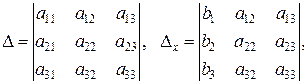 (1.3)
(1.3)
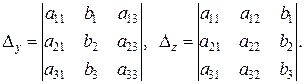 (1.4)
(1.4)
Будем считать, что 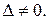
Решением системы является совокупность значений х, у, z, определяемая так называемыми формулами Крамера:
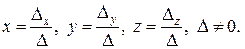
Рассмотрим систему п линейных уравнений с п неизвестными
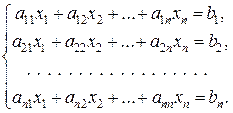
Введем соответствующие этой системе матрицы
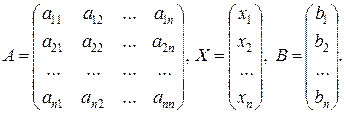
Тогда систему можно записать в матричной форме
АХ = В.
Для решения матричного уравнения умножим обе части этого равенства слева на некоторую матрицу 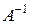 :
:
 (1.5)
(1.5)
а затем подберем (если это удастся) матрицу  так, что
так, что
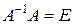 , (1.6)
, (1.6)
где Е – единичная матрица.
Тогда из (1.5) сразу получим решение
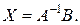
Матрица 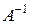 , удовлетворяющая условию (1.6), называется обратной матрицей для матрицы А.
, удовлетворяющая условию (1.6), называется обратной матрицей для матрицы А.
Алгоритм построения обратной матрицы:
1) вычислить det A и убедиться в том, что 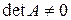 (если det A = 0, обратная матрица не существует);
(если det A = 0, обратная матрица не существует);
|
|
|
2) найти транспонированную матрицу АТ, т. е. матрицу, в которой строки меняются со столбцами (с теми же номерами)
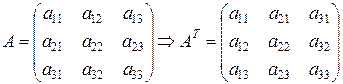 ;
;
3) построить союзную (присоединенную) матрицу 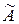 путем замены в матрице АТ каждого элемента его алгебраическим дополнением:
путем замены в матрице АТ каждого элемента его алгебраическим дополнением:
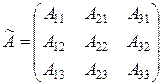 ;
;
4) вычислить обратную матрицу по формуле 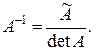
Рассмотрим систему линейных уравнений, содержащую m уравнений с n неизвестными
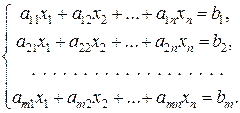
Метод Гаусса (метод последовательного исключения неизвестных) заключается в том, что с помощью элементарных преобразований система линейных уравнений приводится к равносильной системе ступенчатого (или треугольного) вида.
Будем называть элементарными следующие преобразования:
ü перестановка строк местами;
ü умножение элементов какой-либо строки на одно и то же число, не
равное нулю, и прибавление к соответствующим элементам другой строки.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 459; Нарушение авторских прав?; Мы поможем в написании вашей работы!
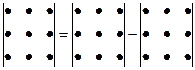 .
.