Дискретні випадкові величини

Випадковою величиною називається така величина, що у результаті випробування може приймати одне зі своїх можливих значень, причому заздалегідь невідомо яке. Наприклад, число народжених дітей протягом доби в Донецьку, зріст людини, витрата електроенергії на підприємстві за місяць, кількість бракованих виробів у партії.

Дискретною називається випадкова величина, що може приймати лише окремі, ізольовані друг від друга значення.

Законом розподілувипадкової величини називається всяке співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини й імовірностями їхньої появи. Закон розподілу можна задавати табличним, графічним, аналітичним способами.

Ряд розподілу – це перелік всіх можливих значень дискретної випадкової величини й відповідних їм імовірностей:

			…
			…

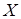
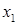
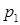
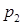
Сума ймовірностей всіх можливих значень дискретної випадкової величини дорівнює одиниці:

. (8.2.1)

Ряд розподілу може бути зображений графічно. Ламану, яку отримаємо, якщо з'єднаємо точки 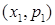,…, відрізками прямих, називають багатокутником розподілу або полігоном.

Інтегральною функцією розподілу (або функцією розподілу) називається функція , що визначає для кожного значення 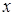імовірність події , тобто

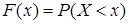. (8.2.2)

Властивості інтегральної функції розподілу:

· Значення інтегральної функції належать відрізку [0;1]:

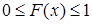. (8.2.3)

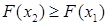· Функція – неспадна, тобто , якщо .

· , .

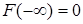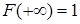· Імовірність того, що випадкова величина 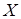прийме значення з напівінтервалу 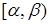(де 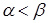), дорівнює різниці значень інтегральної функції на кінцях цього напівінтервалу:

. (8.2.4)

Математичним сподіванням дискретної випадкової величини 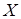називається

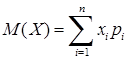. (8.2.5)

Якщо значення дискретної випадкової величини утворюють нескінченну послідовність, то

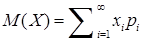. (8.2.6)

Властивості математичного сподівання:

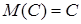· , для постійної величини 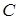; (8.2.7)

· . (8.2.8)

Математичне сподівання є найважливішою з так званих характеристик положення (центра групування) випадкової величини, до яких крім неї належать також мода й медіана. Модою 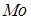дискретної випадкової величини називається те її значення, що має найбільшу ймовірність.

Дисперсією випадкової величини 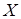називається

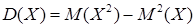. (8.2.9)

Дисперсію дискретної випадкової величини 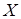з скінченним числом значень n можна обчислити за формулою:

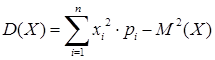. (8.2.10)

Властивості дисперсії:

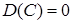· , для постійної величини 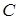; (8.2.11)

· , (8.2.12)

· (для незалежних ). (8.2.13)

Середнім квадратичним відхиленнямвипадкової величини 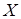називається (арифметичний) корінь квадратний із дисперсії:

. (8.2.14)

Дисперсія й середнє квадратичне відхилення є мірою розсіювання значень випадкової величини навкруг математичного сподівання.

Приклад 8.2.1 У відділі побутової техніки 4 людини. Для кожної людини ймовірність того, що вона звернеться до консультанта, дорівнює 0,4. а) Скласти закон розподілу випадкової величини 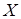– числа людей, які можуть звернутися до консультанта, б) побудувати багатокутник розподілу, в) побудувати інтегральну функцію розподілу і її графік; г) обчислити числові характеристики , , , .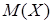

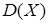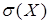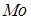Розв’язання. а) Випадкова величина 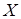– число людей, які можуть звернутися до консультанта – може приймати значення 0, 1, 2, 3, 4. Для кожного можливого значення випадкової величини знайдемо ймовірність за формулою Бернуллі (8.1.15):

; ;

; ; .

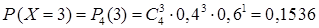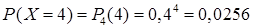Таким чином, ряд розподілу має вигляд:

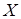
	0,1296	0,3456	0,3456	0,1536	0,0256

Перевірка: 0,1296 + 0,3456 + 0,3456 + 0,1536 + 0,0256 = 1.

б) Багатокутник розподілу ймовірностей має вигляд:

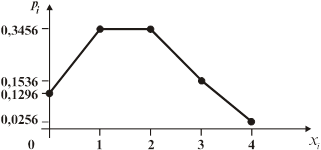
Рис. 8.2.1 ‑ Полігон

в) Побудуємо інтегральну функцію розподілу :

· Нехай . Ліворуч від такого немає значень випадкової величини , значить подія неможлива, а її ймовірність дорівнює нулю, таким чином, .

· Нехай 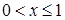. Через те, що випадкова величина 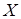може прийняти тільки одне можливе значення 0 з імовірністю 0,1296, то 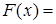0,1296.

· Нехай . У цьому випадку випадкова величина 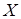може прийняти можливе значення 0 з імовірністю 0,1296, або можливе значення 1 з імовірністю 0,3456. Оскільки ці події несумісні, то за теоремою додавання ймовірностей імовірність події дорівнює сумі ймовірностей цих подій. Тому, щ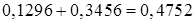о , то .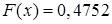

· Нехай . Тоді аналогічно .

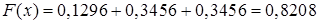· Нехай 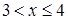. Тоді .

· Нехай . Тоді подія достовірна, значить .

Таким чином, функція розподілу та її графік мають вигляд:

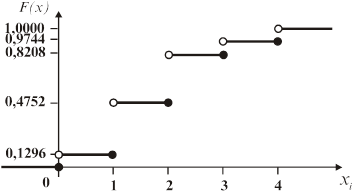
Рис. 8.2.2 – Графік функції розподілу

Графік інтегральної функції розподілу дискретної випадкової величини має східчастий вигляд, розриви при значеннях х, що збігаються з можливими значеннями випадкової величини; величини стрибків дорівнюють значенням ймовірностей, що відповідають можливим значеннями дискретної випадкової величини.

г) Знайдемо математичне сподівання випадкової величини 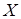та випадкової величини за формулою (8.2.5):

. .

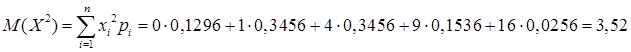Тоді дисперсія згідно (8.2.9): 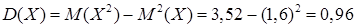, середнє квадратичне відхилення за (8.2.14): . Найбільша ймовірність відповідає двом значенням випадкової величини (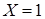 і ), значить розподіл є двомодальним й .

Зауважимо, що приклад 8.2.1 г) відповідає завданню 8.2 контрольної роботи, у якому для обчислення невідомої ймовірності (у другому рядку таблиці розподілу ймовірностей випадкової величини 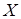) треба застосувати формулу (8.2.1).

Література: [1, с. 516 ‑ 525], [4, с. 529 – 532], [16], [18], [20].

Дата добавления: 2014-12-17