Основные сведения о дифференциальных уравнениях

ТЕМА 8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

.

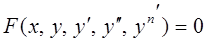Обыкновенным дифференциальным уравнением называется уравнение содержащее независимую переменную х, неизвестную функцию у = у (х) и ее производные: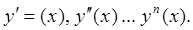

Наивысший порядок производной называется порядком дифференциального уравнения.

Дифференциальное уравнение 1-го порядка:

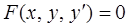или .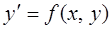

Дифференциальное уравнение 1-го порядка, разрешенное относительно производной можно записать в дифференциальной форме:

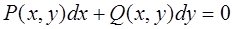
где 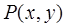и 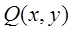- известные функции.

От одного вида записи можно перейти к другому. Интегрирование дифференциального уравнения в общем случае приводит к бесконечному множеству решений, отличающихся константами.

Так решением уравнения 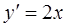является функция y=x², а также y=x²+1 и вообще y=x²+C, 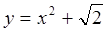и тд.

Чтобы дифференциальное уравнение приобрело конкретный смысл, его надо подчинить некоторым конкретным условиям, называющимся начальными условиями. Начальные условия записываются в виде:

y(x₀)=y₀ или .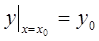

Общим решением дифференциального условия 1-го порядка называется функция 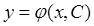содержащая одну произвольную постоянную и удовлетворяющая условиям:

1) Функция 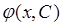является решением дифференциального уравнения при каждом фиксированном значении С.

2) каково бы ни было начальное условие, можно найти такое значение постоянной С=С₀, что функция 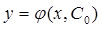удовлетворяет данному начальному условию.

Частным решением дифференциального уравнения 1-го порядка называется любая функция 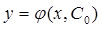полученная из общего решения 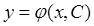при конкретном значении постоянной С=С₀.

Задача отыскания решения дифференциального уравнения 1-го порядка, удовлетворяющего заданному начальному условию 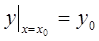называется задачей Коши.

1) Уравнение с разделяющимися переменными:

P(x)dx×Q(y)dy=0,

или P₁(x)×Q₁(y)dx+P₂(x)×Q₂(y)dy=0 произведения двух функций (чисел), где P₁(x)·Q₁(y) и P₂(x)·Q₂(y) – произведения двух функций (чисел).

2) Однородное дифференциальное уравнение.

Дифференциальное уравнение называется однородным, если

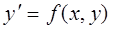
и функция 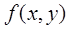есть однородная функция нулевого порядка.

Функция 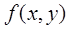называется однородной функцией n-го порядка, если при умножении каждого ее аргумента на произвольный множитель 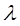вся функция умножается на , т.е.

.

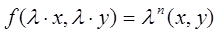Например: функция f (x, y)= x ²-2 xy есть однородная функция 2-го порядка так как

.

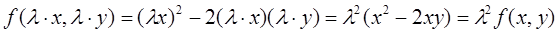Однородные дифференциальные уравнения можно записать в виде:

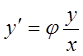
Однородное уравнение часто задается в дифференциальной форме:

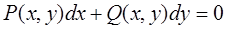
При интегрировании таких уравнений подстановка 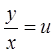или 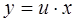сразу преобразует уравнение в уравнение с разделяющимися переменными.

3) Линейное дифференциальное уравнение.

Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде:

,

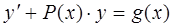где P(x) и g(x) – заданные функции или постоянные.

4) Уравнение Бернулли

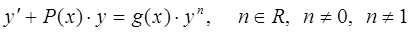
Если n=0, то дифференциальное уравнение – линейное, а если n=1 – с разделяющимися переменными.

Дата добавления: 2014-12-17