Рыночная линия ценной бумаги

Рыночная линия представляет собой равновесное соотношение ожидаемой доходности и среднеквадратичного отклонения для эффективных портфелей. Отдельные рискованные бумаги всегда будут находиться ниже этой прямой, так как единичная рискованная бумага сама по себе является неэффективным портфелем. В модели формирования курсов на фондовом рынке не подразумевается определенной связи между ожидаемой доходностью и среднеквадратичным отклонением (т.е. общим риском) для каждой отдельной ценной бумаги. Для того чтобы сказать больше об ожидаемой доходности, необходим более глубокий анализ.

Ранее было выведено следующее выражение для вычисления среднеквадратичного отклонения для любого портфеля:

где через Х_i и Х_j были обозначены доли инвестиций в бумаги i и j соответственно, а через - ковариация доходностей бумаг i и j. Теперь применим это выражение для вычисления среднеквадратичного отклонения для рыночного портфеля:

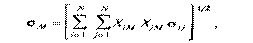
где через Х_i и Х_j обозначены доли инвестиций в бумаги i и j, которые входят в состав рыночного портфеля. Это выражение можно переписать по-другому:

В данной ситуации можно использовать одно из свойств ковариации: ковариация бумаги i с рыночным портфелем () может быть выражена как взвешенное среднее ковариации каждой бумаги с бумагой i:

если применить это свойство к каждой из рискованных бумаг в рыночном портфеле, то в результате получим:

где через обозначена ковариация бумаги 1 с рыночным портфелем, через 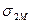- ковариация бумаги 2 с рыночным портфелем и т.д. Таким образом, среднеквадратичное отклонение для рыночного портфеля равно квадратному корню из взвешенного среднeгo ковариаций всех бумаг с рыночным портфелем, где в качестве весов выступают доли инвестиций в бумаги, входящие в состав этого портфеля.

В САРМ каждый инвестор обладает рыночным портфелем и его интересует среднеквадратичное отклонение своего портфеля, так как от него будет зависеть наклон CML, а следовательно, и размер инвестиций инвестора в рыночный портфель. Вклад каждой бумаги в среднеквадратичное отклонение рыночного портфеля, как видно из последнего уравнения, зависит от величины ковариаций бумаги с рыночным портфелем. В соответствии с этим для каждого инвестора становится понятным, что величина допустимого риска каждой бумаги определяется ковариацией этой бумаги с рыночным портфелем, . Это означает, что инвесторы будут рассматривать бумаги с большим значением , как вносящие больной риск в рыночный портфель. Кроме того, отсюда также следует, что бумаги, среднеквадратичное отклонение которых велико, не обязательно вносят больше риска в рыночный портфель, чем бумаги с меньшей величиной среднеквадратичного отклонения.

Из этого следует, что ценные бумаги с большими значениями siM должны обеспечивать пропорционально большую ожидаемую доходность, что должно заинтересовать инвестора в их приобретении. Для того чтобы понять, почему так происходит, рассмотрим ситуацию, когда бумаги с большим значением , не обеспечивают инвесторам соответствующего уровня ожидаемой доходности. В такой ситуации получается, что эти бумаги вносят большую долю риска в рыночный портфель, не обеспечивая вместе с тем пропорционального увеличения ожидаемой доходности рыночного портфеля. Это означает, что при изъятии таких ценных бумаг из рыночного портфеля ожидаемая доходность портфеля по отношению к среднеквадратичному отклонению будет возрастать. А так как инвесторы сочтут такое изменение выгодным, то рыночный портфель перестанет быть оптимальным рискованным портфелем, а курсы ценных бумаг не будут находиться в равновесном состоянии.

Точная форма равновесной взаимосвязи между риском и доходом может быть записана в следующем виде:

На левом рисунке данное уравнение описывает прямую, пересекающую вертикальную ось в точке с ординатой r и имеющую наклон . Так как величина наклона положительна, то уравнение указывает на то, что курсы ценных бумаг с большим значением ковариаций с рыночным портфелем будут обеспечивать большую ожидаемую доходность r_i. Эта зависимость ковариции и ожидаемой доходности известна под названием рыночная линия ценной бумаги (Security Market Line, SML).

Интересен тот факт, что рискованная ценная бумага с будет иметь ожидаемую доходность, равную ставке процента безрисковой бумаги, r_f. Объясняется это тем. что такая рискованная бумага, так же как и безрисковая, не добавляет риска в рыночный портфель. Это так, несмотря на то, что рискованная бумага имеет положительное среднеквадратичное отклонение, а у безрисковой бумаги оно нулевое.

Возможно даже, что ожидаемая доходность некоторых рискованных бумаг (имеются в виду бумаги с положительным среднеквадратичным отклонением) окажется ниже, чем безрисковая ставка. Согласно САРМ, это имеет место, когда , т.е. ценные бумаги вносят отрицательную величину риска в рыночный портфель (это означает, что вносимый ими в рыночный портфель риск меньше, чем в случае, когда в эти бумаги инвестируется меньше средств).

Другим примечательным фактом является также то, что рискованная бумага с 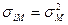будет иметь ожидаемую доходность, равную ожидаемой доходности рыночного портфеля. Это связано с тем, что такая бумага вносит среднюю величину риска в рыночный портфель.

Уравнение SML может быть записано также и в следующей форме:

где под понимается следующее:

.

Величина называется коэффициентом “бета” (или просто “бетой”) для бумаги i и является альтернативным способом представления ковариаций бумаги. Предыдущее уравнение представляет собой иную форму записи уравнения SML, что видно из правого рисунка. Хотя обе прямые пересекают ось ординат в одной и той же точке, они имеют различный наклон. Наклон прямой, описанной последним уравнением, равен , а описанной первым уравнением SML - .

Одно из свойств коэффициента “бета” портфеля заключается в том, что он представляет собой взвешенное среднее коэффициентов “бета” входящих в него ценных бумаг, где в качестве весов выступают доли инвестиций в эти бумаги. Выражение для вычисления коэффициента “бета” портфеля выглядит следующим образом:

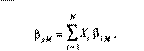
Ранее было показано, что ожидаемая доходность портфеля представляет собой взвешенную среднюю ожидаемых доходностей входящих в его состав ценных бумаг, где в качестве весов представлены доли инвестирования в эти бумаги. Это означает, что так как каждая бумага лежит на SML, то на этой же прямой будет лежать и каждый портфель. Но, точнее, не только каждая бумага, но и каждый портфель должны находиться на прямой, имеющей положительный наклон, где в качестве оси ординат выбрана ожидаемая доходность, а в качестве оси абсцисс — коэффициент “бета”. Следовательно, получается, что эффективные портфели лежат как на CML, так и на SML, а неэффективные лежат на SML, но ниже CML.

Следует отметить, что SML должна проходить через точку, изображающую рыночный портфель. Значение “беты” для этой точки равно 1, а ожидаемая доходность равна 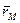, т.е. ее координатами являются пара 1 и 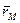. Так как значение коэффициента “бета” безрисковых бумаг равно нулю, то SML должна проходить так же через точку с координатами 0 и r_f, т.е. должна пересекать вертикальную ось в точке с ординатой r_f. Теперь легко вычислить наклон SML как разницу ординат этих точек , деленную на разницу их абсцисс (1 — 0), в итоге наклон равен . Эти две точки, которые определяют положение прямой SML, представляют собой приемлемые ожидаемые доходности ценных бумаг и портфелей с различными значениями “беты”. Равновесное состояние, представленное SML, складывается в результате суммарного эффекта корректировки инвесторами структуры своих портфелей и результирующего давления на курсы бумаг. Обладая набором курсов ценных бумаг, инвесторы вычисляют ожидаемые доходности и ковариации, а затем определяют состав своих оптимальных портфелей. Если спрос на ценные бумаги какого-либо вида отличен от их предложения, то такая несбалансированность будет оказывать воздействие на их курс. Получив новую информацию о курсах, инвесторы пересмотрят свои намерения относительно различных бумаг. Этот процесс будет продолжаться до тех пор, пока общий спрос на ценные бумаги какого-либо вида не уравновесит их предложение, Для отдельного инвестора курс ценных бумаг и их перспективы заданы, а их количество он может менять. Для рынка же в целом количество бумаг фиксированно (по крайней мере, в короткий промежуток времени), а их курсы постоянно меняются. Как и на любом конкурентном рынке, для достижения равновесия на рынке ценных бумаг необходима корректировка курсов бумаг до тех пор, пока не установится соответствие между спросом на бумаги и их предложением, вполне логичным представляется обратиться к доходностям бумаги за прошедший период времени, для того чтобы определить, был ли ее курс сформирован в равновесии, как предполагалось в САРМ. Однако вопрос о том, можно ли осуществить такую проверку разумными методами, является спорным. Кроме того, при решении некоторых задач в рамках САРМ нет необходимости в таких проверках.

Выводы

1. Модель САРМ основана на ряде предположений о поведении инвестора и существовании совершенных фондовых рынков.

2. Исходя из этих предположений, портфели рискованных активов у всех инвесторов будут одинаковы.

3. Инвесторы различаются лишь размерами осуществляемого ими безрискового заимствования или кредитования.

4. Общий для всех инвесторов портфель рискованных активов называется рыночным портфелем.

5. Рыночный портфель включает все ценные бумаги, причем доля каждой ценной бумаги равна отношению ее рыночной стоимости к суммарной рыночной стоимости всех ценных бумаг.

6. Линейное эффективное множество в модели САРМ называется рыночной линией (CML). Эта прямая отображает равновесную зависимость между ожидаемыми доходностями и стандартными отклонениями эффективных портфелей.

7. Согласно САРМ, подходящей мерой риска ценной бумаги является ее ковариация с рыночным портфелем.

8. Линейное соотношение ковариации и ожидаемой доходности известно как рыночная линия ценной бумаги (SML).

9. Альтернативной мерой риска, вносимого ценной бумагой в рыночный портфель, является коэффициент “бета” этой бумаги. Значение “беты” равно отношению ковариации бумаги и рыночного портфеля к дисперсии рыночного портфеля.

10. Величины коэффициентов “бета” в модели САРМ и в рыночной модели сходны по смыслу. Однако в отличие от САРМ рыночная модель не является моделью равновесия финансового рынка. Более того, рыночная модель использует рыночный индекс, который в общем случае не охватывает рыночный портфель, используемый в САРМ.

11. Согласно САРМ, совокупный риск ценной бумаги складывается из рыночного и нерыночного рисков. В соответствии с рыночной моделью нерыночный риск связан только с данной ценной бумагой и поэтому называется собственным рисков

Дата добавления: 2014-11-29