Отношения

Между элементами множеств можно установить отношения в виде их произведения. Декартовым произведением множеств А и В называют множество AxB всех упорядоченных пар элементов (а;b), где 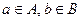, т.е. . Элементы a и b при этом называют компонентами (координатами) пары.

Пример: . Тогда

.

Декартово произведение АxА называется декартовым квадратом множества А.

В целях наглядного представления декартовых произведений удобно использовать язык геометрии. Для этого множества X,Y представляются осями координат. Элементы 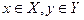-- соответственно абсциссами и ординатами. Само произведение -- точками плоскости XOY. Любое непустое подмножество такого произведения называется бинарным отношением. Ему можно придать прикладное значение. Например, значения множества X – названия предметов, изучаемых в университете, а элементы множества Y – группы студентов. Тогда отношению XxY можно придать смысл множества изучаемых студентами предметов.

По аналогии с декартовым произведением двух множеств X,Y можно построить декартово произведение XxYxZ трех и более множеств. Пример может быть следующий: по курсу x студент y выбрал билет z.

Бинарные отношения обладают следующими свойствами:

-- рефлексивность – отношение Р, при котором элемент отображается сам на себя, т.е. для любого x из Х выполняется xРx. Например, «x похож на x».

-- антирефлексивность – отношение, противоположное рефлексивности, т.е. xРx не выполняется ни для одного x из X. Например, «скорость компьютера x больше компьютера x». Данное отношение – скорость одного компьютера больше другого – обладает свойством антирефлексивности, т.к. скорость одного и того же компьютера не может превышать саму себя.

-- симметричность – отношение, при котором xРy влечет yРx. Например, отношение «x похож на y» обладает свойством симметричности, т.к. верно, что и «y похож на x». Отношение же «компьютер x быстрее y» не симметрично, т.к. «компьютер y быстрее x» уже не выполняется.

-- асимметричность – отношение, обратное симметричности, т.е. одно из двух соотношений xPy или yPx не выполняется. Отношение «компьютер x быстрее y» асимметрично.

-- антисимметричность – отношение, при котором xPy и yPx выполняются тогда и только тогда, когда x=y. Отношение «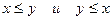» выполняется только тогда, когда x=y.

-- транзитивность – отношение, при котором, из xPy и yPz следует xPz. Например, из того, что «студент В пришел позже студента А» и «студент С пришел позже студента В» следует, что «студент С пришел позже студента А».

Отношение Р называют отношением эквивалентности, если оно одновременно рефлексивно, транзитивно и симметрично.

Пример. Р – отношение равенства треугольников – отношение эквивалентности.

Отношение называют частичного (нестрогого) порядка, если оно одновременно рефлексивно, антисимметрично и транзитивно.

Пример. 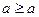- рефлексивность

выполняются одновременно, когда 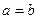- антисимметричность

Если , то - транзитивность.

Следовательно, отношение «» есть отношение частного порядка.

Отношение Р называют отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.

Пример. Отношение «<» на множестве чисел являются отношениями строгого порядка.

Задачи.

1. Заданы множества , тогда декартовым произведением этих множеств является множество...

Варианты ответов:

2. Выяснить, являются ли следующие отношения отношениями эквивалентности:

а) равенство в произвольной системе множеств;

b) отношение параллельности прямых;

с) отношение «проживания в одном доме» жителей города;

d) ;

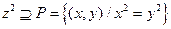e) .

3. Привести примеры отношений:

а) рефлексивного и симметричного, но не транзитивного в некотором множестве;

б) рефлексивного и транзитивного, но не симметричного;

в) симметричного и транзитивного, но не рефлексивного.

Дата добавления: 2014-11-29