
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основное уравнение динамики точки
|
|
|
|
Основное уравнение динамики материальной точки представляет собой не что иное, как математическое выражение второго закона Ньютона:
 , (4.14)
, (4.14)
где сила  в общем случае является суммой ряда сил, действующих на материальную точку.
в общем случае является суммой ряда сил, действующих на материальную точку.
Уравнение (4.14) есть, это по существу дифференциальное уравнение движения точки в векторном виде. Его решение - основная задача динамики материальной точки. При этом возможны две противоположные постановки задачи.
Первая задача. Найти закон действующей на точку силы  , если известны масса т точки и зависимость от времени ее радиус-вектора
, если известны масса т точки и зависимость от времени ее радиус-вектора 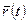 .
.
Здесь решение задачи сводится к дифференцированию уравнения (4.14).
Задача 4.1
Движение материальной точки массы 0,2кг выражается уравнениями 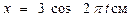 ,
,  (t в секундах). Определить проекции силы, действующей на точку, в зависимости от ее координат.
(t в секундах). Определить проекции силы, действующей на точку, в зависимости от ее координат.
Решение. Записываем дифференциальные уравнения движения точки: 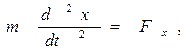

Вычисляем требующиеся производные:
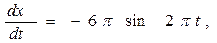


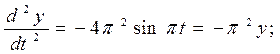
Теперь можно определить искомые проекции силы:
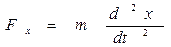 = - 0,2 * 4 * 3,142 * 0,01х = - 0,0789 х (Н),
= - 0,2 * 4 * 3,142 * 0,01х = - 0,0789 х (Н),
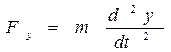 = - 0,2 * 3,142 * 0,01у = - 0,0197 у (Н),
= - 0,2 * 3,142 * 0,01у = - 0,0197 у (Н),
причем х и у должны быть выражены в метрах.
Вторая задача. Найти закон движения точки, т. е. зависимость от времени ее радиус-вектора 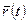 , если известны масса т точки, действующие на нее силы
, если известны масса т точки, действующие на нее силы 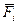 и начальные условия - скорость
и начальные условия - скорость 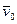 и положение
и положение 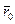 точки в начальный момент времени. Решение задачи сводится к интегрированию по времени.
точки в начальный момент времени. Решение задачи сводится к интегрированию по времени.
Задача 4.2
Материальная точка массы т совершает прямолинейное движение под действием силы, изменяющейся по закону. F = Fo cosωt, где Fo и ω - постоянные величины. В начальный момент точка имела скорость 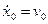 . Найти уравнение движения точки.
. Найти уравнение движения точки.
Решение. В случае прямолинейного движения точки дифференциальное уравнение движения имеет вид:
|
|
|

а начальными условиями в нашей задаче будут: t = 0; х = х0 = 0; v = dx/dt = v0.
Имеем 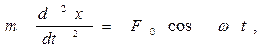
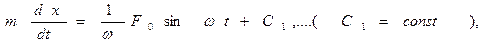

Определяем из начальных условий постоянные C1 и С2: 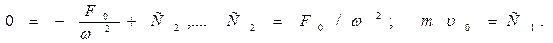
Подставляя найденные значения постоянных в общее решение дифференциального уравнения, находим закон движения точки:

или 
Математическая сторона решения этих задач достаточно подробно была рассмотрена в кинематике точки.
В зависимости от характера и постановки конкретной задачи решение уравнения (4.14) проводят или в векторной форме, или в координатах, или в проекциях на касательную и нормаль к траектории в данной точке. Выясним, как записывают уравнение (4.14) в последних двух случаях.
В проекциях на декартовы координаты. Проектируя обе части уравнения(4.14) на оси X, Y, Z, получим три дифференциальных уравнения вида
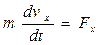 ,
, 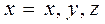 , (4.15)
, (4.15)
где Fx, Fy, Fz - проекции вектора  на оси X, Y, Z.
на оси X, Y, Z.
Необходимо помнить, что эти проекции - величины алгебраические: в зависимости от ориентации вектора  они могут быть как положительными, так и отрицательными. Знак проекции результирующей силы
они могут быть как положительными, так и отрицательными. Знак проекции результирующей силы  определяет и знак проекции ускорения.
определяет и знак проекции ускорения.
Задача 4.3
Небольшой брусок массы т скользит вниз по наклонной плоскости, составляющей угол α с горизонтом. Коэффициент трения между бруском и плоскостью равен f. Найти ускорение бруска относительно плоскости (эта система отсчета предполагается инерциальной).
Решение Прежде всего, следует изобразить все силы, действующие на брусок. Это сила тяжести 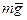 , сила нормальной реакции
, сила нормальной реакции 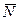 со стороны плоскости и сила трения
со стороны плоскости и сила трения 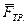 (рис. 4.4), направленная вверх - в сторону, противоположную движению бруска.
(рис. 4.4), направленная вверх - в сторону, противоположную движению бруска.
 После этого свяжем с системой отсчета «наклонная плоскость» систему координат X,Y, Z. Вообще говоря, систему координат можно ориентировать как угодно, однако во многих случаях (и, в частности, в данном) выбор направления осей диктуется характером движения. В данном случае, например, заранее известно направление движения бруска, поэтому наиболее целесообразно оси координат расположить так, чтобы одна из них совпадала с направлением движения. Тогда задача сведется к решению только одного уравнения (4.15). Итак, выберем ось х, как показано на рис. 4.4, обязательно указав при этом ее положительное направление (стрелкой).
После этого свяжем с системой отсчета «наклонная плоскость» систему координат X,Y, Z. Вообще говоря, систему координат можно ориентировать как угодно, однако во многих случаях (и, в частности, в данном) выбор направления осей диктуется характером движения. В данном случае, например, заранее известно направление движения бруска, поэтому наиболее целесообразно оси координат расположить так, чтобы одна из них совпадала с направлением движения. Тогда задача сведется к решению только одного уравнения (4.15). Итак, выберем ось х, как показано на рис. 4.4, обязательно указав при этом ее положительное направление (стрелкой).
|
|
|
И только теперь можно приступить к составлению уравнений (4.15): слева — произведение массы т бруска на проекцию его ускорения ax и справа - проекции всех сил на ось х:
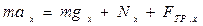 .
.
В данном случае 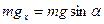 ,
,  и
и 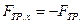 , поэтому
, поэтому
 .
.
Так как брусок движется только вдоль оси х, то это значит, согласно второму закону Ньютона, что сумма проекций всех сил на любое перпендикулярное к оси х направление равна нулю. Взяв в качестве такого направления ось Y (см. рис. 4.4), получим
 .
.
В результате
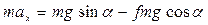 .
.
Если правая часть этого уравнения окажется положительной, то и 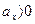 , а это значит, что вектор
, а это значит, что вектор 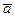 направлен вниз по наклонной плоскости, и наоборот.
направлен вниз по наклонной плоскости, и наоборот.
 В проекциях на касательную и нормаль к траектории в данной точке. Проектируя обе части (4.14) на подвижные орты
В проекциях на касательную и нормаль к траектории в данной точке. Проектируя обе части (4.14) на подвижные орты 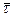 и
и 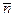 (рис. 4.5) и используя полученные ранее выражения (3.10) для тангенциального и нормального ускорений, запишем
(рис. 4.5) и используя полученные ранее выражения (3.10) для тангенциального и нормального ускорений, запишем
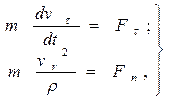 (4.16)
(4.16)
где Fτ и Fn - проекции вектора  на орты
на орты 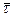 и
и 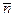 . На рис.4.5 обе проекции положительные. Векторы
. На рис.4.5 обе проекции положительные. Векторы 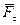 и
и  называют тангенциальной и нормальной составляющими силы
называют тангенциальной и нормальной составляющими силы  .
.
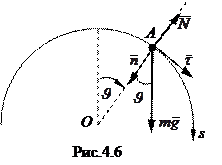 Напомним, что направление орта
Напомним, что направление орта 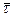 выбирают в сторону возрастания дуговой координаты s, а направление орта
выбирают в сторону возрастания дуговой координаты s, а направление орта 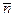 - к центру кривизны траектории в данной точке.
- к центру кривизны траектории в данной точке.
Уравнениями (4.16) удобно пользоваться, если заранее известна траектория материальной точки.
Задача 4.4
Небольшое тело А соскальзывает с вершины гладкой сферы радиуса r. Найти скорость тела в момент отрыва от поверхности сферы, если его начальная скорость пренебрежимо мала.
Решение Изобразив силы, действующие на тело А (это сила тяжести 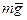 и нормальная сила реакции
и нормальная сила реакции 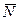 ), запишем уравнения (3.16) в проекциях на орты
), запишем уравнения (3.16) в проекциях на орты 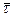 и
и 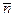 .(рис.4.6):
.(рис.4.6):
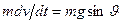 , (1)
, (1)
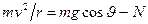 . (2)
. (2)
Преобразуем первое уравнение к виду, удобному для интегрирования. Воспользовавшись тем,
что 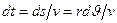 , где ds - элементарный путь тела А за промежуток времени dt, перепишем первое уравнение в виде
, где ds - элементарный путь тела А за промежуток времени dt, перепишем первое уравнение в виде
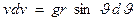 .
.
Проинтегрировав это выражение (левую часть - по v от 0 до v правую - по υ - от 0 до υ), найдем
|
|
|
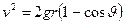 .
.
Далее, в момент отрыва N = 0, поэтому (2) исходное уравнение принимает вид
 ,
,
где v и υ соответствуют точке отрыва. Исключив cos υ из последних двух равенств, получим  .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 5770; Нарушение авторских прав?; Мы поможем в написании вашей работы!