Потенциальное поле сил

Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке, например поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.

Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. Однако, среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками 1 и 2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в механике. К изучению этих свойств мы и перейдем.

Поясним сказанное на примере следящей силы. На рис. 5.4 изображено тело ABCD, в точке О которого приложена сила , неизменно связанная с телом.

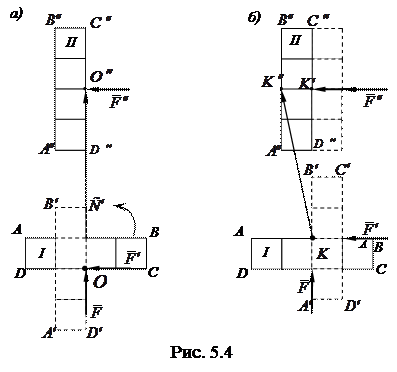Переместим тело из положения I в положение II двумя способами. Выберем вначале в качестве полюса точку О (рис. 5.4а)) и повернем тело вокруг полюса на угол π/2 противоположно направлению вращения часовой стрелки. Тело займет положение A'B'C'D'. Сообщим теперь телу поступательное перемещение в вертикальном направлении на величину ОО". Тело займет положение II (A"B"C"D"). Работа силы на совершенном перемещении тела из положения I в положение II равна нулю. Вектор перемещения полюса представлен отрезком ОО".

При втором способе выберем в качестве полюса точку K рис. 5.4б) и повернем тело вокруг полюса на угол π/2 против движения часовой стрелки. Тело займет положение A'B'C'D' (рис. 5.4б). Теперь переместим тело вертикально вверх с вектором перемещения полюса KK', после чего дадим телу горизонтальное перемещение влево на величину K'K". В результате тело займет положение II, такое же, как на позиции, рис.5.4 а)рисунка 5.4. Однако теперь вектор перемещения полюса будет иным, чем в первом способе, а работа силы при втором способе перемещения тела из положения I в положение II равна А = F К'К", т. е. отлична от нуля.

Определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называют потенциальным, а сами силы – консервативными.

Потенциалом таких сил (потенциальной энергией)называется работа, совершенная ими на перемещениях тела из конечного положения в начальное, причем начальное положение может быть выбрано произвольно. Это означает, что потенциальная энергия определяется с точностью до постоянной.

Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называются неконсервативными.

В реальных механических системах всегда имеются силы, работа которых при действительном движении системы отрицательна (например, силы трения). Такие силы называются диссипативными. Они являются частным видом неконсервативных сил.

Консервативные силы обладают рядом замечательных свойств, для выявления которых введем понятие силового поля. Силовым полем называется пространство (или его часть), в котором на материальную точку, помещенную в каждую точку этого поля, действует некоторая сила.

Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части, 1а2 и 2b1. Так как поле потенциально, то, по условию, 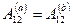. С другой стороны, очевидно, что 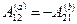. Поэтому

,

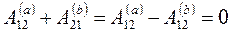что и требовалось доказать.

Обратно, если работа сил поля на любом замкнутом пути равна нулю, то работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства возьмем два произвольных пути 1а2 и 1b2 (см. рис. 5.5). Составим из них замкнутый путь 1а2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. 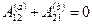. Отсюда 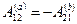. Но 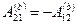, поэтому

.

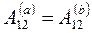Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться отличительным признаком любого потенциального поля сил.

Поле центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Силы, зависящие только от расстояния между взаимодействующими частицами и направленные по прямой, соединяющей эти частицы, называют центральными. Примером последних являются силы гравитационные, кулоновские и упругие.

Центральную силу, действующую на частицу А со стороны частицы В, можно представить в общем виде:

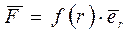, (5.8)

где f (r) - функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами; 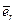- единичный вектор, задающий направление радиуса-вектора частицы А относительно частицы В (рис. 5.6).

Докажем, что всякое стационарное поле центральных сил потенциально.

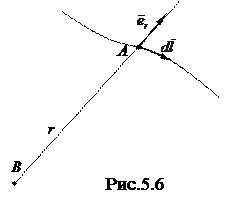Для этого рассмотрим сначала работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы В. Элементарная работа силы (5.8) на перемещении 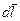есть 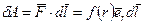. Так как 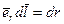- проекция вектора 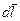на вектор 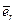, или на соответствующий радиус-вектор (рис. 5.6), то 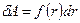. Работа же этой силы по произвольном пути от точки 1 до точки 2

.

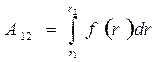Полученное выражение зависит, только от вида функции f (r), т. е. от характера взаимодействия, и от значений r₁ и r₂ начального и конечного расстояний между частицами А и В. От формы пути оно никак не зависит. А это значит, что данное силовое поле потенциально.

Обобщим полученный результат на стационарное силовое поле, вызванное наличием совокупности неподвижных частиц, действующих на частицу А с силами 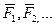, каждая из которых является центральной. В этом случае работа результирующей силы при перемещении частицы А из одной точки в другую равна алгебраической сумме работ отдельных сил. А так как работа каждой из этих сил не зависит от формы пути, то и работа результирующей силы от нее также не зависит.

Таким образом, действительно, любое стационарное поле центральных сил потенциально.

Потенциальная энергия частицы. То обстоятельство, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.

Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек Р_i в фиксированную точку О. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки Р (при фиксированной точке О). А это значит, что данная работа будет некоторой функцией радиус-вектора 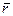точки Р. Обозначив, эту функцию 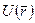, запишем

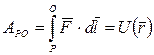. (5.9)

Функцию 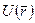называют потенциальной энергией частицы в данном поле.

Теперь найдем работу сил поля при перемещении частицы из точки 1 в точку 2 (рис. 5.7). Так как работа не зависит от пути, возьмем путь проходящий через точку 0. Тогда работа на пути 1 0 2 может быть представлена в виде

,

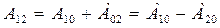или с учетом (5.9)

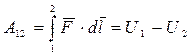(5.10)

Выражение, стоящее справа, есть убыль* потенциальной энергии, т. е. разность значений потенциальной энергии частицы в начальной и конечной точках пути.

_________________

* Изменение какой-либо величины X можно характеризовать либо ее приращением, либо убылью. Приращением величины X называют разность конечного (X₂) и начального (Х₁) значений этой величины:

приращение Δ Х = Х₂ - Х₁.

Убылью величины X называют разность ее начального (Х₁) и конечного (Х₂) значений:

убыль Х₁ — Х₂ = - Δ Х,

т. е. убыль величины X равна ее приращению, взятому с обратным знаком.

Приращение и убыль - величины алгебраические: если Х₂ > X₁, то приращение положительно, а убыль отрицательна, и наоборот.

Таким образом, работа сил поля на пути 1 - 2 равна убыли потенциальной энергии частицы.

Очевидно, частице, находящейся в точке 0 поля, всегда можно приписать любое наперед выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что путем измерения работы может быть определена лишь разность потенциальных энергий в двух точках поля, но не ее абсолютная величина. Однако как только фиксировано значение

потенциальной энергии в какой-либо точке, значения ее во всех остальных точках поля однозначно определяются формулой (5.10).

Формула (5.10) дает возможность найти выражение 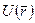для любого потенциального поля сил. Для этого достаточно вычислить работу, совершаемую силами поля на любом пути между двумя точками, и представить ее в виде убыли некоторой функции, которая и есть потенциальная энергия .

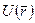Именно так и было сделано при вычислении работы в полях упругой и гравитационной (кулоновской) сил, а также в однородном поле тяжести [см. формулы (5.3) — (5.5)]. Из этих формул сразу видно, что потенциальная энергия частицы в данных силовых полях имеет следующий вид:

1) в поле упругой силы

, (5.11)

2) в поле точечной массы (заряда)

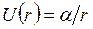, (5.12)

3) в однородном поле тяжести

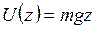. (5.13)

Еще раз подчеркнем, что потенциальная энергия U - это функция, которая определяется с точностью до прибавления некоторой произвольной постоянной. Это обстоятельство, однако, совершенно несущественно, ибо во все формулы входит только разность значений U в двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает. В связи с этим ее обычно опускают, что и сделано в трех предыдущих выражениях.

И еще одно важное обстоятельство, о котором не следует забывать. Потенциальную энергию, строго говоря, следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. При данном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел.

Связь между потенциальной энергией и силой. Согласно (5.10), работа силы потенциального поля равна убыли потенциальной энергии частицы, т. е. А ₁₂ = U ₁ - U ₂ = - (U ₂ — U ₁). При элементарном перемещении 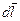последнее выражение имеет вид dА = - dU, или

F_l dl= — dU. (5.14)

Отсюда

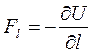(5.15)

т. е. проекция силы поля в данной точке на направление перемещения 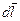равна с обратным знаком частной производной потенциальной энергии по данному направлению.

Символ 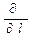частной производной — подчеркивает, что производная берется по определенному направлению. Соотношение (5.15) справедливо для любого направления в пространстве, в частности, и для направлений декартовых осей координат. В этом случае (5.15) определяет проекции вектора на оси X, Y, Z. Но если известны эти проекции, то оказывается определенным и сам вектор :

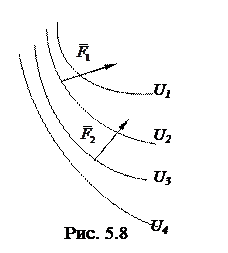
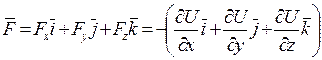
Величину, стоящую в скобках, называют градиентом функции U и обозначают grad U. Таким образом,

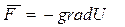, (5.16)

что означает: сила поля равна с обратным знаком градиенту потенциальной энергии. Таким образом, если известна функция 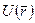, то с помощью формулы (5.16) мы имеем возможность восстановить поле сил .

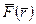Геометрическое место точек в пространстве, в которых потенциальная энергия U имеет одно и то же значение, определяет эквипотенциальную поверхность. Ясно, что каждому значению U соответствует своя эквипотенциальная поверхность.

Из формулы (5.15) следует, что проекция вектора на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор нормален к эквипотенциальной поверхности в данной точке. Кроме того, знак минус в (5.15) означает, что вектор направлен в сторону уменьшения потенциальной энергии. Сказанное поясняет рис. 5.8, относящийся к двумерному случаю; здесь изображена система эквипотенциалей, причем U₁ < U₂ < U₃ < ….

Дата добавления: 2014-11-29