Закон сохранения энергии системы

До сих пор мы ограничивались рассмотрением поведения одной частицы с энергетической точки зрения. Теперь перейдем к системе частиц. Это может быть любое тело, газ, любой механизм, Солнечная система и т. д.

В общем случае частицы системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. Систему частиц, на которую не действуют никакие посторонние тела, называют замкнутой (или изолированной). Понятие замкнутой системы является естественным обобщением понятия изолированной материальной точки и играет важную роль в механике.

Потенциальная энергия системы. Рассмотрим замкнутую систему, между частицами которой действуют только центральные силы, т. е. силы, зависящие при данном характере взаимодействия только от расстояния между частицами и направленные по прямой, их соединяющей.

Покажем, что в любой системе отсчета работа всех этих сил при переходе системы частиц из одного положения в другое может быть представлена как убыль некоторой функции, зависящей при данном характере взаимодействия только от конфигурации самой, системы, или от относительного расположения ее частиц. Эту функцию назовем собственной потенциальной энергией системы (в отличие от потенциальной энергии, характеризующей взаимодействие данной системы с другими телами).

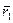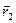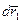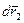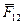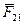Сначала возьмем систему из двух частиц. Вычислим элементарную работу сил, с которыми эти частицы взаимодействуют между собой. Пусть в произвольной системе отсчета в некоторый момент времени положение частиц определяется радиус-векторами и . Если за время dt частицы совершили перемещения и соответственно, то работа сил взаимодействия и равна

.

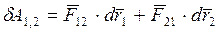Теперь учтем, что согласно третьему закону Ньютона 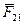= - 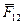, поэтому предыдущее выражение можно переписать так:

Введем вектор 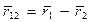, характеризующий положение 1-й частицы относительно 2-й. Тогда 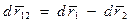и после подстановки в выражение для работы получим

.

Сила 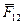- центральная, поэтому работу этой силы можно представить в виде убыли потенциальной энергии взаимодействия данной пары частиц, т. е.

.

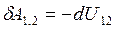Так как функция U₁₂ зависит только от расстояния 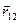между частицами, то ясно, что работа δА_1,2 не зависит от выбора системы отсчета.

Теперь обратимся к системе из трех частиц (полученный в этом случае результат легко обобщить и на систему из произвольного числа частиц). Элементарная работа, которую совершают все силы взаимодействия при элементарном перемещении всех частиц, может быть представлена как сумма элементарных работ всех трех пар взаимодействий, т. е. . Но для каждой пары взаимодействий, как было показано, 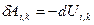, поэтому

,

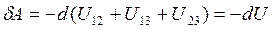где функцию U называют собственной потенциальной энергией данной системы частиц:

.

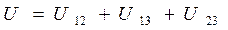Так как каждое слагаемое этой суммы зависит от расстояния между соответствующими частицами, то очевидно, что собственная потенциальная энергия U данной системы зависит от относительного расположения частиц, или, другими словами, от конфигурации системы.

Ясно, что подобные рассуждения справедливы и для системы из любого числа частиц. Поэтому можно утверждать, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия U, и работа всех центральных сил при изменении этой конфигурации равна убыли собственной потенциальной энергии системы, т. е.

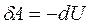, (5.27)

а при конечном перемещении всех частиц системы

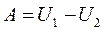, (5.28)

где U₁ и U₂ - значения потенциальной энергии системы в начальном и конечном состояниях.

Важно отметить, что собственная потенциальная энергия системы U - величина неаддитивная, т. е. она не равна в общем случае сумме собственных потенциальных энергий ее частей. Необходимо учесть еще потенциальную энергию взаимодействия U_B3 отдельных частей системы:

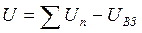, (5.29)

где U_n — собственная потенциальная энергия п -й части системы.

Следует также иметь в виду, что собственная потенциальная энергия системы, как и потенциальная энергия взаимодействия каждой пары частиц, определяется с точностью до прибавления произвольной постоянной, которая, впрочем, и здесь совершенно несущественна.

В заключение приведем полезные формулы для расчета собственной потенциальной энергии системы. Прежде всего, покажем, что эта энергия может быть представлена как

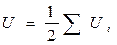(5.30)

где U_i - потенциальная энергия взаимодействия i -й частицы со всеми остальными частицами системы. Здесь сумма берется по всем частицам системы.

Убедимся в справедливости этой формулы сначала для системы из трех частиц. Выше было показано, что собственная потенциальная энергия данной системы 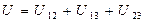. Преобразуем эту сумму следующим образом. Представим каждое слагаемое U_ik в симметричном виде: 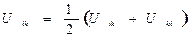, ибо ясно, что U_ik = U_ki. Тогда

.

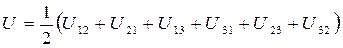Сгруппируем члены с одинаковым первым индексом:

.

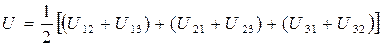Каждая сумма в круглых скобках представляет собой потенциальную энергию U_i. взаимодействия i -й частицы с остальными двумя. Поэтому последнее выражение можно переписать так:

,

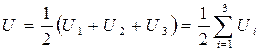что полностью соответствует формуле (5.30).

Обобщение полученного результата на произвольную систему очевидно, ибо ясно, что подобные рассуждения совершенно не зависят от числа частиц, составляющих систему.

Кинетическая энергия системы. Рассмотрим в некоторой системе отсчета произвольную систему частиц. Пусть i -я частица системы имеет в данный момент кинетическую энергию T_i. Приращение кинетической энергии каждой частицы равно согласно (3.18) работе всех сил, действующих на эту частицу: dT_i =δA_i. Найдем элементарную работу, которую совершают все силы, действующие на все частицы системы:

,

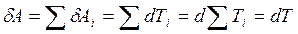где 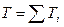, т. е. представляет собой суммарную кинетическую энергию системы.

Заметим, что кинетическая энергия системы - величина аддитивная: кинетическая энергия системы равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они между собой или нет.

Итак, приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. При элементарном перемещении всех частиц

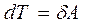, (5.31)

а при конечном перемещении

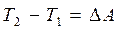(5.32)

Эти две формулы выражают закон изменения кинетической энергии всей системы. Этот закон можно представить и в другой форме, поделив обе части (5.31) на соответствующий промежуток времени dt. Имея при этом в виду, что 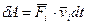, получим

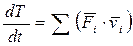, (5.33)

где правая часть - это суммарная мощность всех сил, действующих на все частицы системы.

Классификация сил. В общем случае частицы рассматриваемой системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. В соответствии с этим силы взаимодействия между частицами рассматриваемой системы называют внутренними, а силы, обусловленные действием других тел, не входящих в данную систему, - внешними. В неинерциальной системе отсчета к последним относят и силы инерции.

Кроме того, все силы делят на потенциальные и непотенциальные. Потенциальными называют силы, зависящие при данном характере взаимодействия только от конфигурации механической системы. Работа этих сил, как было показано, может быть представлена как убыль потенциальной энергии системы.

К непотенциальным силам относятся так называемые гироскопические и диссипативные силы.

Гироскопические силы, примером которых является сила Лоренца, отличаются тем, что их работа всегда равна нулю; поэтому в дальнейшем они не будут нас интересовать.

Диссипативные силы - это силы трения и сопротивления. Важной особенностью этих сил является то, что суммарная работа внутренних диссипативных сил рассматриваемой системы отрицательна, причем в любой системе отсчета. Докажем это.

Любая диссипативная сила может быть представлена в виде

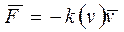, (5.34)

где - скорость данной частицы относительно другой частицы (или среды), с которой она взаимодействует; k(v) — положительный коэффициент, зависящий в общем случае от скорости v.

Сила всегда направлена противоположно вектору . В зависимости от выбора системы отсчета работа этой силы может быть как положительной, так и отрицательной. Суммарная же работа всех внутренних диссипативных сил - величина всегда отрицательная.

Переходя к доказательству этого, отметим, прежде всего, что внутренние диссипативные силы в данной системе будут встречаться попарно, причем в каждой паре согласно третьему закону Ньютона они одинаковы по величине и противоположны по направлению. Найдем элементарную работу произвольной пары диссипативных сил взаимодействия между частицами 1 и 2 в системе отсчета, где скорости этих частиц в данный момент равны 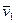и :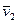

.

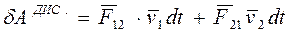Теперь учтем, что 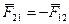, скорость частицы 1 относительно частицы 2, а также то, что 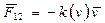. Тогда выражение для работы можно преобразовать так:

.

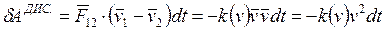Отсюда видно, что работа произвольной пары внутренних диссипативных сил взаимодействия всегда отрицательна, а раз так, то и суммарная работа всех пар внутренних диссипативных сил также всегда отрицательна. Таким образом, действительно,

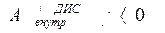. (5.35)

Законы изменения и сохранения энергии системы. Выше было показано, что приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. Разделив эти силы на внешние и внутренние, а внутренние, в свою очередь, - на потенциальные и диссипативные, запишем предыдущее утверждение так:

.

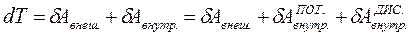Теперь учтем, что работа внутренних потенциальных сил может быть представлена в виде убыли собственной потенциальной энергии системы, т.е. 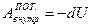. Тогда предыдущее выражение примет вид

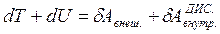(5.36)

Введем понятие полной механической энергии системы, или, короче, механической энергии, как сумму кинетической и потенциальной энергии системы:

E = T + U. (5.37)

Очевидно, энергия Е зависит от скоростей частиц системы, характера взаимодействия между ними и от конфигурации системы. Кроме того, энергия Е, как и потенциальная энергия U, определяется с точностью до прибавления несущественной произвольной постоянной и является величиной неаддитивной, т. е. энергия Е системы не равна в общем случае сумме энергий ее отдельных частей. В соответствии с (5.29)

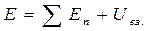, (5.38)

где Еп — механическая энергия n -й части системы, U_вз - потенциальная энергия взаимодействия ее отдельных частей.

Вернемся к формуле (3.36). Перепишем ее с учетом (5.37) в виде

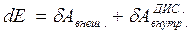. (5.39)

Это выражение справедливо при бесконечно малом изменении конфигурации системы. При конечном же изменении

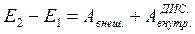(5.40)

Последние две формулы выражают закон изменения энергии системы: приращение механической энергии системы равно алгебраической сумме работ всех внешних и внутренних диссипативных сил.

Этот закон можно представить и в другой форме, поделив обе части (5.39) на соответствующий промежуток времени dt. Тогда

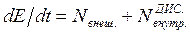(5.41)

т. е. производная механической энергии системы по времени равна алгебраической сумме мощностей всех внешних и внутренних диссипативных сил.

Из закона изменения энергии системы непосредственно вытекает один из важнейших законов механики - закон сохранения энергии замкнутой системы. А именно: если в замкнутой системе диссипативные силы отсутствуют, то ее полная механическая энергия сохраняется в процессе движения, т. е.

Е = Т + U = const. (5.42)

Такую систему называют консервативной. Заметим, что при движении замкнутой консервативной системы сохраняется именно полная механическая энергия, кинетическая же и потенциальная в общем случае изменяются. Однако эти изменения происходят всегда так, что приращение одной из них в точности равно убыли другой, т. е. Δ T = —Δ U.

Необходимо также отметить, что понятие замкнутой консервативной системы- это идеализация. Таких систем в окружающем нас мире, строго говоря, нет. Наиболее хорошим приближением является Солнечная система. В земных же условиях благодаря неизбежному наличию диссипативных сил консервативные системы реализуются лишь грубо приближенно. И тем не менее во многих случаях использование понятия замкнутой консервативной системы - условия (5.42) - позволяет получать ответы на ряд вопросов с достаточно высокой степенью точности.

Далее, из того же закона изменения энергии системы следует, что если замкнутая система неконсервативна, т. е. в ней имеются диссипативные силы, то полная механическая энергия такой системы согласно (5.35) убывает:

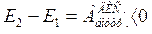
Это, однако, не противоречит универсальному закону сохранения энергии: при уменьшении механической энергии замкнутой системы всегда возникает эквивалентное количество энергии других видов, не связанных с видимым движением. Сюда относятся кинетическая энергия беспорядочного движения атомов и молекул, химическая энергия, энергия излучения и др.

И, наконец, полная механическая энергия может сохраняться и в незамкнутых системах, но лишь в тех случаях, когда, как следует из формулы (3.40), уменьшение ее за счет работы внутренних диссипативных сил компенсируется поступлением энергии за счет работы внешних сил.

При решении конкретных задач необходимо всегда помнить, что разделение сил на внешние и внутренние зависит от выбора интересующей нас системы частиц (тел). Только после того, как система выбрана, можно говорить, какие силы внешние и какие внутренние. Разумеется, от выбора системы будет зависеть и характер решения. Проиллюстрируем это на следующем примере.

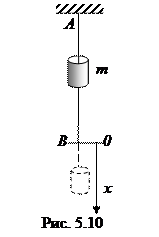
Задача 5.5

Имеется невесомая упругая нить длиной l, закрепленная одним концом в точке А (рис. 5.10). Из точки А без начальной скорости падает небольшая муфта массы т. Дойдя до упора В, муфта, продолжая движение, начала растягивать нить. Найти коэффициент упругости с нити, если к моменту остановки муфты нить удлинилась на Δ l. Трение отсутствует.

Здесь возможны три способа решения в зависимости от выбора системы.

Решение. 1. Если в качестве рассматриваемой системы взять только муфту, то все силы, действующие на нее, являются внешними. Это сила тяжести и упругая сила. В начальном и конечном положениях муфты ее кинетическая энергия равна нулю, поэтому согласно А_тяж + А_упр = 0, или

.

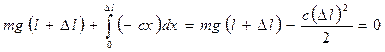Отсюда

.

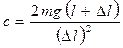2. Теперь возьмем в качестве системы муфту и Землю (без нити), В этом случае сила тяжести будет внутренней силой, а упругая сила - внешней. Согласно (5.40), приращение полной энергии данной системы Е₂ - Е ₁= 0. Распишем это выражение, учитывая, что его левая часть равна только приращению потенциальной энергии гравитационного взаимодействия муфты и Земли:

.

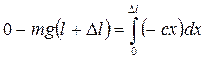Отсюда получим тот же результат.

3. И наконец, включим в рассматриваемую систему и нить. Тогда все силы оказываются внутренними, и система является замкнутой. Для нее приращение полной энергии Е равно нулю, а оно складывается только из приращений потенциальной энергии гравитационного взаимодействия и потенциальной энергии упругой деформации нити, т.е, Δ E= Δ U_гр. + Δ U_упр. = 0, или

.

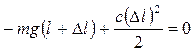Результат опять тот же.

В заключение отметим еще два существенных обстоятельства.

1. В неинерциальных системах отсчета закон изменения механической энергии имеет тот же вид, что и (5.40) или (5.41). Однако в этих системах отсчета под работой внешних сил надо понимать не только работу внешних сил взаимодействия 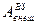, но и работу сил инерции А_ин.. Отсюда, в частности, следует, что в неинерциальных системах отсчета замкнутых систем частиц не существует.

2. При решении большинства задач закон сохранения энергии применяют обычно совместно с законами сохранения или импульса, или момента импульса, или с тем и другим одновременно. Как это делается, будет показано в следующих двух главах.

Вывод

Рассмотрены законы сохранения энергии применительно к различным механическим объектам. Подробно изложены правила определения потенциальной и кинетической энергий для систем и частиц. Описаны такие элементы энергии, как работа и мощность, Приведены примеры определения работы для некоторых наиболее распространенных механических сил. Указаны некоторые характерные свойства сил применительно к энергетическому состоянию тел.

Контрольные вопросы

1. Назовите первопричины законов сохранения основных механических величин.

2. Определите кинетическую энергию тела и системы.

3. От чего зависит изменение энергии объекта?

4. Какое силовое поле называют стационарным?

5. Приведите классификацию сил силового поля.

6. Дайте определения консервативным и диссипативным силам.

7. Сформулируйте наиболее простой закон сохранения энергии системы.

8. За счёт чего может измениться кинетическая энергия системы тел?

9. Как выбор системы отсчёта влияет на работу взаимодействия двух частиц?

10. Что общего и в чём различие внешних и внутренних сил?

ГЛАВА 6 ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Дата добавления: 2014-11-29