Регрессионного анализа 2 страница

Для построения модели вида (3.36) осуществим кодирование входных факторов, построим матрицу планирования ПФЭ 2³ и после рандомизации проведем 24 опыта с использованием математический модели движения центра масс снаряда.

Матрица планирования и результаты вычислительного эксперимента приведены в таблице 3.4.

Таблица 3.4. – Матрица планирования и результаты вычислительного эксперимента

№ опыта	Кодированные входные факторы	Выходной параметр
x0	x1	x2	x3	y1	y2	y3
	+ + + + + + + +	- + - + - + - +	- - + + - - + +	- - - - + + + +	-88 -405 -28 -350	-72 -429 -15 -362	-63 -392 -41 -310

В таблице 3.4. приняты следующие обозначения:

X₀ – фиктивная переменная;

X₁ – фактор 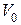в кодированном виде;

X₂ – фактор в кодированном виде;

X₃ – фактор С в кодированном виде;

y _ij, где i -1.8; j -1.3 – значения выходного параметра в метрах и в ij- опыте.

В качестве входных неуправляемых случайных факторов, создающих «шум» при проведении вычислительного эксперимента, были заданы случайные воздействия внешней среды – метеофакторы, как суммы соответствующих постоянных и случайных составляющих.

2 Проверка возможности проведения обработки результатов эксперимента методом множественного регрессионного анализа.

Выполнение основных предпосылок возможности проведения регрессионного анализа предопределено порядком проведения эксперимента. Так как эксперимент вычислительный, то ошибка фиксации (измерения) значений входных исследуемых факторов равна нулю. «Шум» эксперимента является случайной величиной, распределенной по нормальному закону с параметрами N(M[ 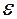] = 0, 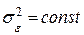), так как разброс метеофакторов моделировался нормальным законом распределения. Следовательно, и выходной параметр Д - также будет подчиняться данному закону распределения (это следует из-за того, что в результате композиции нескольких нормальных законов получается нормальное суммарное распределение). Таким образом, следует проверить предпосылку – однородность оценок дисперсии выходного параметра.

Как было отмечено ранее, фактически это проверка постоянства дисперсии «шума»:

.

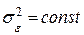Считается, что это условие выполнено, если справедлива гипотеза:

.

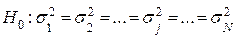Проверка данной гипотезы при конкурирующей H ₁ хотя бы одна дисперсия 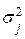не равна остальным, для одинакового числа параллельных опытов в каждой точке плана эксперимента, производится с помощью критерия Кохрена. Статистика G этого критерия имеет вид:

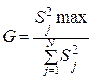, (3.37)

где – оценка дисперсии выходного параметра для j -го опыта.

Например, для первого опыта имеем:

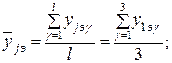
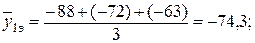
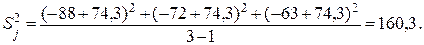
Проведя аналогично вычисления, получим оценки и , значения которых приведены в таблице 3.5.

Таблица 3.5 – Исходный материал для проверки однородности оценок

дисперсий

№ опыта
Оценка	-74,3	-408,7	-28,0	-341,0	350,7	43,3	347,3	93,0
Оценка	160,3	352,3	169,0	751,0	324,3	444,3	466,3	351,0

Определяем расчетное значение G - критерия по формуле (3.37):

.

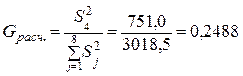С целью проверки нулевой гипотезы H ₀: 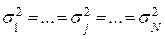по таблице значений G – критерия (приложение А) выбираем его критическое табличное значение для уровня значимости l = 0.05 числа степеней свободы f = l – 1 = 3 – 1 = 2 и числа суммируемых оценок дисперсий, равного N:

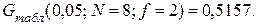
Сравниваем расчетное и табличное значение G – критерия.

.

Так как расчетное значение меньше табличного критического значения, то гипотеза об однородности ряда выборочных дисперсий выходного параметра не отвергается. Это означает, что значимых различий и в качестве оценки дисперсии воспроизводимости эксперимента можно взять среднюю дисперсию, то есть:

;

.

Таким образом, все предпосылки для проведения множественного регрессионного анализа выполняются и можно приступить к расчету коэффициентов уравнения регрессии.

3 Определяем оценки коэффициентов регрессии:

,

,

,

,

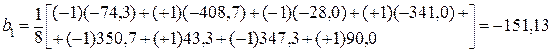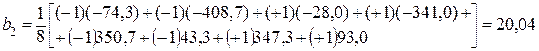Таким образом, уравнение приближенной регрессии будет иметь вид:

.

4 Проводим статистический анализ уравнения регрессии.

Проверка адекватности уравнения регрессии результатам эксперимента:

Определим значения оценок выходного параметра 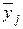по результатам вычислений с использованием полученного уравнения приближенной регрессии:

Вычисляем оценку дисперсии адекватности:

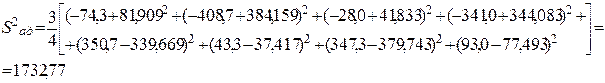
Вычисляем расчетное значение F -критерия:

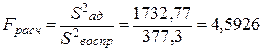
C целью проверки статистической гипотезы вида:

определяем из таблицы приложения Б критическое значение F – критерия для уровня значимости α = 0.05 и степеней свободы числителя

f ₁ = N – h = 8 – 4 = 4

и знаменателя f ₂ = 16;

.

Сравниваем расчетное и табличное значения F – критерия:

F_расч. = 4,5926 > F_табл. = 3,7294.

Так как расчетное значение F – критерия больше табличного, то гипотеза об адекватности полученного значения приближенной регрессии экспериментальным данным отвергается.

Как было отмечено выше, в данном случае можно уменьшить интервалы варьирования факторов, выбрать другую базовую точку либо перейти к нелинейной модели – к полиному второго порядка. Однако в рассматриваемых условиях целесообразно учесть, что один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. ПФЭ позволяет количественно оценить все эффекты взаимодействия факторов. Дополнительных экспериментов при этом проводить не требуется, следует лишь расширить исходную матрицу планирования. Вид такой матрицы приведен в таблице 3.6.

Таблица 3.6 – Расширенная матрица планирования ПФЭ 2³

№ опыта	Кодированные входные факторы	Выходной параметр
X0	X1	X2	X3	X1X2	X1X3	X2X3	X1X2X3
	+	-	-	-	+	+	+	-	-74,3
	+	+	-	-	-	-	+	+	-408,7
	+	-	+	-	-	+	-	+	-28,0
	+	+	+	-	+	-	-	-	-341,0
	+	-	-	+	+	-	-	+	350,7
	+	+	-	+	-	+	-	-	43,3
	+	-	+	+	-	-	+	-	347,3
	+	+	+	+	+	+	+	+	93,0

5 Определяемоценки коэффициентов регрессии при взаимодействиях факторов.

Планирование по матрице, представленной в таблица 3.6, позволяет получить математическую модель вида:

.

Определяем неизвестные оценки коэффициентов регрессии:

Выполняя аналогичные вычисления, можно получить следующие величины оценок коэффициентов регрессии: b₁₃ = +10.7; b₂₃ = -8.46; b₁₂₃ = +3.96.

Записываем аналогичные вычисления приближенной регрессии:

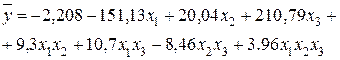
6 Проводим статистический анализ уравнения регрессии.

Так как в полученном уравнении число оцениваемых коэффициентов регрессии равно числу опытов N и степеней свободы для проверки его адекватности нет, то статистический анализ начнем с проверки значимости коэффициентов.

6.1 Проверка значимости оценок коэффициентов регрессии.

C целью проверки статистической гипотезы вида:

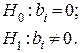
определяем из таблицы приложения Г критическое значение t – критерия для уровня значимости 0.05 и числа степеней свободы:

Сравниваем расчетные значения t – критерия с критическим табличным значением. Коэффициенты, для которых выполняется условие

,

следует признать статистически значимыми и оставить в уравнении регрессии, а все остальные исключить.

Уравнение регрессии принимает вид:

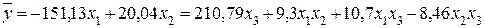
6.2 Проверка адекватности уравнения регрессии результатам эксперимента.

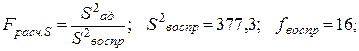
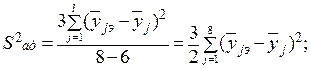
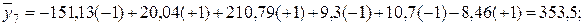
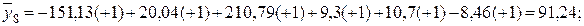
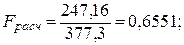
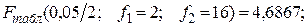
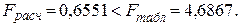
Таким образом, полученное уравнение приближенной регрессии адекватно описывает исследуемый процесс, то есть математическая модель (полином) хорошо согласуется с экспериментальными данными.

7 Интерпретация уравнения регрессии.

Обработав результаты ПФЭ, мы получили уравнение приближенной регрессии (полином первой степени)

которое адекватно описывает зависимость отклонения центра группирования снарядов от точки прицеливания до дальности Д от ошибок определения основных баллистических параметров 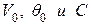. Коэффициенты данного уравнения являются частными производными выходного параметра по соответствующим переменным. Их геометрический смысл – тангенсы углов наклона гиперплоскости к соответствующей оси.

Поэтому больший по абсолютной величине коэффициент соответствует большему углу наклона и, следовательно, более существенному изменению выходного параметра при изменении данного фактора.

Анализ величин коэффициентов регрессии показывает, что преобладающий вклад в выходной параметр вносит фактор x₃ -ошибка определения баллистического коэффициента С и фактор 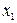-ошибка определения начальной скорости полета снаряда 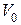. Следует отметить, что наряду с линейными эффектами на величину Д оказывают влияние и парные взаимодействия факторов, вклад которых в исследуемый процесс незначителен и приблизительно одинаков.

Так как величину отклонения центра группирования снарядов от точки прицеливания за счет ошибок определения основных баллистических параметров следует минимизировать, то благоприятным является увеличение фактора x₁ и уменьшение факторов x ₂ и x ₃. Для уменьшения влияния взаимодействий факторов x ₁, x ₂, x ₃данные факторы должны изменяться одновременно в разных направлениях. Учитывая влияние линейных эффектов, следует фактор x ₁ увеличивать, а x ₂ и x ₃ уменьшать. Коэффициент регрессии при взаимодействии x ₂ x ₃имеет знак минус, поэтому для уменьшения влияния данного эффекта следует одновременно увеличивать или уменьшать факторы x ₂ и x ₃. С учетом влияния их линейных эффектов следует одновременно уменьшить данные факторы.

Следует отметить, что результаты интерпретации иногда могут расходиться с априорными теоретическими представлениями об изучаемом процессе. В этом случае (при корректном эксперименте) нужно иметь в виду, что эксперимент проводится в локальной области факторного пространства, и коэффициенты регрессии отражают влияние факторов только в этой области. Заранее неизвестно, в какой мере можно распространить полученный результат на другие области, а теоретические представления имеют обычно более общий характер. Кроме того, априорная информация часто основывается на однофакторных зависимостях. При переходе к многофакторному пространству ситуация может измениться.

На заключительном этапе интерпретации можно построить уравнение регрессии для натуральных значений факторов, то есть осуществить обратный переход от безразмерной к размерной системе координат.

По полученному уравнению можно предсказывать (вычислять) величину отклонения центра группирования снарядов от точки прицеливания до дальности Д при изменении входных исследуемых факторов 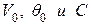в пределах области экспериментирования.

Дата добавления: 2014-11-29