Приклад 2. 2 страница

і критерії , ,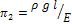

де — відносна подовжинна деформація;

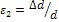— відносна поперечна деформація;

— модуль Юнга; ρ — щільність матеріалу конструкції;

F — характерна зовнішня сила; g — прискорення сили тяжіння.

Критерії подібності в електричній системі

Хай електричний ланцюг складається з двох резисторів R₁ і R₂ і джерела ЕРС Е. Згідно другого закону Кірхгофа:

.

Представимо це рівняння у вигляді: .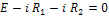

Робимо рівняння безрозмірним: .

Звідси критерії подібності: ; .

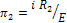Всяка нова комбінація з критеріїв подібності також є критерієм подібності, що дає можливість у кожному конкретному випадку вибрати найбільш зручні і характерні критерії.

Хай процес описується рівнянням F(x,y,q) = 0. Тоді критерії подібності:

Тут

де α_i, β_j, γ_к можуть набувати довільних значень, у тому числі і нульові.

У конкретному випадку, якщо, наприклад, процес описується інтегральним рівнянням F(x,y,q) = E – iR₁, - iR₂ = 0 маємо {q} = {R₁,R₂},

{x} = Е, {у} = i. Приведення до безрозмірного вигляду дає

1 – iR₁/E - iR₂/E = 0. Це означає, що для всіх подібних процесів повинна виконуватися умова

π₁ = iR₁ /E = 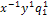= const,

π₂ = iR₂ /E = = const.

Звідси: С₁ = С₂ = 1; ; т.е. α₁ = α₂ = -1.

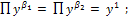т.е. β₁ = β₂ = 1.

; т.е. γ₁ = 1.

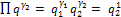; т.е. γ₁ = 0; γ₂ = 1.

Якщо відомі рівняння, що описують дане фізичне явище, то критерії подібності для цього явища можна отримати, приводячи рівняння до безрозмірного вигляду шляхом введення деяких характерних значень для кожного з визначальних фізичних параметрів, що входять в систему рівнянь. Тоді критерії подібності визначаться як безрозмірні коефіцієнти, що з'являються перед деякими з членів нової, безрозмірної системи рівнянь. Коли рівняння, що описують фізичне явище, невідомі, критерії подібності відшукуються за допомогою аналізу размерностей, що визначають фізичні параметри.

2.4 Теореми подібності

Забезпечення достовірності отриманих по модельних дослідженнях результатів при проведенні обмеженого числа експериментів при різноманітних поєднаннях параметрів вимагає необхідних і достатніх умов для існування подібності. Ці умови відбиті в трьох теоремах подібності, в яких сконцентрований результат численних досліджень. Перші дві теореми визначають необхідні, третя – необхідні і достатні умови подібності.

Перша теорема подібності, звана теоремою Ньютона або Ньютона—Бертрана, затверджує: що для подібних явищ повинні існувати однакові критерії подібності. У основному сучасному формулюванні, що враховує можливість існування різних видів подібності, перша теорема має наступний вигляд: явища, подібні в тому або іншому сенсі (повно, приблизно, фізично, математично і т. д.), мають певні поєднання параметрів, звані критеріями подібності, чисельно однакові для подібних явищ.

Перша теорема не указує способи встановлення подібності і способи його реалізації, вона лише формує необхідні умови існування подібності (однакові критерії подібності).

Друга теорема подібності, звана π – теоремою, затверджує: всяке повне рівняння фізичного процесу, записане в певній системі одиниць, може бути представлене функціональною залежністю між критеріями подібності, отриманими з параметрів цього процесу. Друга теорема встановлює можливість представлення інтеграла диференціального рівняння фізичного процесу не як функції параметрів процесу і системи, в якій протікають ці процеси, а як функція відповідним чином побудованих деяких безрозмірних величин — критеріїв подібності. Якщо початкове диференціальне рівняння проінтегрувало, то функціональні зв'язки між критеріями подібності будуть однозначно визначені відповідно до тих допущень, які були прийняті при складанні і інтеграції даного рівняння. Якщо ж диференціальне рівняння було відсутнє або не інтегрувалося, то вид функціональних зв'язків між критеріями подібності не буде виявлений. Пізніше, проте, Еренфест-афанасьева привела доказ того, що критерії подібності можна знайти і за відсутності диференціального рівняння процесу на основі аналізу размерностей фізичних величин, що беруть участь в цьому процесі. Ця можливість була сформульована і строго доведена у вигляді теореми, названою π-теоремой, оскільки згадані вище безрозмірні параметри (критерії подібності) позначалися буквою π.

Друга теорема так само, як і перша, не указує способів виявлення подібності і способів реалізації подібності.

Третя теорема подібності визначає необхідні і достатні умови подібності фізичних явищ. Третя теорема подібності утверж дає: необхідними і достатніми умовами для створення подібності явища, що вивчається, є:

· пропорційність подібних параметрів, що входять в умови однозначності;

· рівність критеріїв подібності явища, що вивчається.

Умови однозначності – це умови, що визначають індивідуальні особливості досліджуваного явища. Ці умови не залежать від механізму самого досліджуваного явища.

До них відносяться наступні чинники і умови:

· геометричні властивості системи, в якій протікає процес;

· фізичні параметри середовища і тіл, створюючих систему;

· початковий стан системи (початкові умови);

· умови на межах системи (граничне або краєві умови);

· взаємодія об'єкту і зовнішнього середовища.

Очевидно, не можна математично формулювати умови однозначності в загальному вигляді. У кожному конкретному випадку вони можуть бути різні залежно від роду вирішуваного завдання і виду рівняння. Так, наприклад диференціальне рівняння u = iR + Ldi/dt описує зміну струму в часі у ланцюзі з активним опором R і індуктивністю L при включенні її на u = const. Для виділення певного процесу з сукупності процесів, що описуються приведеним рівнянням, достатньо знати параметри u, R, L і початкові умови, наприклад,

i = i₀ при t = t₀.

Третя теорема подібності іменується також зворотною теоремою подібності або теоремою Кирпічева—Гухмана.

2.5 Аналіз розмірностей

Аналіз розмірностей виник як результат природного розповсюдження на фізичні явища понять геометричної подібності, відношення і пропорції. Дж. Фурье (1768–1830) вперше встановив, що існують певні основні одиниці вимірювання, щодо яких кожна фізична величина має визначені розмірності, які потрібно записувати як показники ступенів основних одиниць вимірювання.

Ідеї, лежачі в основі аналізу розмірностей, по суті очевидні і прості і базуються на фізичних законах (зв'язках між фізичними величинами), вони не залежать від свавілля у виборі основних одиниць вимірювання. З цієї ідеї на основі простих міркувань і застосування простого математичного апарату можна вивести важливе слідство: функції, які виражають фізичні закономірності, повинні володіти деякою фундаментальною властивістю, яка в математиці називається узагальненою однорідністю або симетрією. Ця властивість дозволяє записати шукані закономірності в безрозмірному вигляді, інваріантному щодо вибору систем одиниць вимірювання, з меншим числом аргументів (вже безрозмірних) і тим самим спростити їх (закономірностей) знаходження.

Одиниця вимірювання є мірою, за допомогою якої вимірюється та або інша фізична величина. Цим вимірюванням є пряме або непряме порівняння фізичних характеристик з відповідними (фізично подібними) еталонами, прийнятими за одиницю і званими одиницею вимірювання. Так, період напіврозпаду порівнюється з одиницею вимірювання – роком, швидкість літака порівнюється з одиницею вимірювання швидкості, рівній швидкості рівномірного руху, в якому шлях в один кілометр проходиться за час, рівний одній годині і так далі.

Величини, чисельні значення яких в даних питаннях залежать від вибору одиниць вимірювання, називаються розмірними величинами. Наприклад, енергію можна вимірювати в кілограмометрах, калоріях, тоннах вугілля, кілограмах урану, рублях і ще в багатьох інших одиницях вимірювання.

Одиниці вимірювання фізичних величин підрозділяються на основних і похідних. Величини, для яких одиниці вимірювання вводяться з досвіду за допомогою природних або штучних еталонів, по умові називаються первинними або основними. При цьому самі одиниці вимірювання також називаються первинними. Так, наприклад, для вивчення механічних рухів відомими способами вводяться первинні, або основні, одиниці вимірювання, такі, як довжина, час і маса, причому тут є певна свобода вибору. Так, для опису тих же механічних явищ можна прийняти еталони для сили, довжини і часу.

Одиниці вимірювання для інших величин, які виходять з визначення цих величин через первинних, називаються похідними або вторинними. Визначення фізичної величини завжди указує спосіб її вимірювання, принаймні уявний. Так, щільністю, згідно визначенню, є відношення маси до величини об'єму, який її укладає.

У різних областях науки і техніки вигідно і зручно вибирати як первинні одиниці вимірювання свої місцеві системи первинних одиниць вимірювання. Системою одиниць вимірювання називається сукупність основних одиниць вимірювання, достатня для вимірювання параметрів (характеристик) даного класу явищ. Виникли різні системи одиниць вимірювання і як наслідок – рутинне завдання про перехід (перерахунку) від однієї системи до іншої.

З 1960 року використовується Міжнародна система одиниць СІ (System International d’Unites), в якій основними одиницями вимірювання є метр, кілограм-маса і секунда.

Вираз похідної одиниці вимірювання через основні одиниці вимірювання називається її розмірністю. Розмірність виражає якісну суть фізичної величини, зміряної за допомогою даної системи одиниць вимірювання, і виходить автоматично з визначення цієї величини. Для позначення розмірності фізичних величин вводять символи. У системі СІ символи одиниць вимірювання для основних фізичних величин будуть: L для одиниці довжини, T для одиниці часу і M для одиниці маси. Розмірність деякої фізичної величини f прийнято за пропозицією Максвела позначати через [ f ]. Важливо підкреслити, що розмірність визначається класом систем одиниць вимірювання і в різних класах систем вимірювання розмірність одної і той же фізичної величини буде різною. Так, наприклад, розмірність сили F вкласі LMT буде [F] = MLT ^-2, а в класі MKS, де основними є метр, кілограм - сила и секунда, вона буде [F] = K. Таким чином, у формулі (у функції) розмірності для якої-небудь величини φ,

[φ] = L^α T ^β M ^γ. (2.4)

Аргументи L, T, M виступають як деякі позитивні числа, які можна перемножувати або ділити.

Величини, чисельне значення яких однаково у всіх системах одиниць вимірювання усередині даного класу, називаються безрозмірними, тобто для таких величин в (2.4) α = β = γ = 0. Очевидно, що розмірність безрозмірної величини рівна одиниці. Останні всі величини називаються розмірними.

Приведена вище формула (функція) розмірності фізичної величини (2.4) є степеневий одночлен. Природно виникає питання: чи є фізичні величини, для яких це не так, тобто їх розмірність наприклад в класі LTM, виражається у вигляді M sin L або lg T / e^M ? Насправді таких величин немає і розмірність будь-якої фізичної величини завжди є степеневим одночленом.

Говорять, що набір величин а₁ , а₂ ,…, а_к мають незалежні розмірності, якщо розмірність жодної з цих величин не можна представити у вигляді добутку ступенів розмірностей решти величин. Наприклад, розмірності щільності [ρ] = ML ^-3, прискорення [w] = LT ^-2 і сили [F] = MLT ^-2 незалежні; розмірності довжини [l] = L швидкості [v] = LT ^-1 і прискорення [w] = LT ^-2 залежні, оскільки між размерностями цих останніх величин має місце співвідношення [l] • [w] = [ v ² ].

Приклад 1.

Кожному фізикові доводилося застосовувати методи аналізу розмірностей до простих задач, зокрема в області механіки.

Почнемо з дуже показової задачі про простий математичний маятник.

Наша мета — знайти без детального рішення задачі деякі співвідношення між різними вимірюваними величинами, які представляють для нас інтерес. Звичайний метод полягає в наступному. Перш за все виписується таблиця величин, від яких, ймовірно, залежить відповідь, далі складаються формули розмірності цих величин і, нарешті, накладається умова, щоб ці величини входили у функціональні зв'язки, не залежні від одиниць, в яких величини зміряні.

Спробуємо цим методом знайти залежність періоду коливання простого маятника змінних, які визначають його властивості. Очевидно, час коливання може залежати від довжини маятника, його маси, прискорення сили тяжіння і амплітуди коливань. Випишемо розмірності цих величин, застосовуючи основну систему одиниць – СІ. Таблиця величин в даному випадку має такий вигляд:

Назва величини Символ Формула

розмірності

Час коливання t T

Довжина маятника l L

Маса маятника m M

Прискорення сили тяжіння g LT ^-2

Кутова величина коливання θ без розмірності

Ми повинні виразити t як функцію l, m, g и T так, щоб функціональне співвідношення залишалося незмінним при будь-якій зміні розміру основних одиниць. Хай це співвідношення має вигляд:

t = f (l, m, g, θ)

Формули розмірностей показують, яким чином основні одиниці визначають чисельне значення змінних. Чисельна величина періоду коливання залежить тільки від вибраної одиниці часу і не міняється при зміні одиниць маси або довжини. Отже, величини, які стоять под знаком f у правій частині рівняння, повинні бути асоційовані так, щоб вся комбінація залишалася незмінної при зміні одиниць маси і довжини. Зокрема, не повинна відбутися зміна при зміні одиниці тільки одної маси. Але розмір одиниці маси впливає тільки на величину m. Тому, якщо взагалі m входить в аргумент функції, то чисельне значення функції буде іншим при зміні основної одиниці маси, причому ця зміна не може компенсуватися відповідною зміною значень інших кількостей, оскільки останні не залежать від зміни розміру одиниці маси. Отже маса взагалі не може входити у функціональне співвідношення, інакше кажучи, наша функція приймає вигляд:

t = f (l, g, θ).

Величини l і g разом повинні входити у функцію так, щоб числове значення аргументу не мінялося при зміні одиниці довжини і постійному t, тобто зміна числової величини l, здійснюване зміною розміру одиниці довжини повинно в точності компенсуватися зміною значення g, що відбувається при такій зміні одиниць. Формула розмірності показує, що для виконання цього необхідно розділити l на g тобто:

.

Далі, зміна основних одиниць не може вплинути на числову величину кутової амплітуди, оскільки вона не має розмірності і отже, θ може входити в невідому функцію будь-яким способом.

Але очевидно, що l / g повинно бути представлено у функції так, щоб вся комбінація мала розмірність Т, оскільки таку розмірність має t, яке стоїть в лівій частині. Звідси ясно, що l / g повинно знаходитися під знаком квадратного кореня, тобто

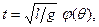
де φ(θ) – невідома функція.

Далі по міркуваннях симетрії (явище не залежить від правого або лівого початкового відхилення маятника на кут θ₀) виходить, що

φ(θ₀) = φ (- θ₀ ), тобто функція φ парна. При малих θ функцію φ можна розкласти в ряд

φ(θ) = C₁ + C₂ θ + C₃ θ ² + … = C₁ + C₃ θ ³ + …

Тут прийнято C₂ = 0 через парність функції φ. Для малих коливань члени з ступенями θ ² і вище можна опустити, і тоді для періоду малих коливань получим формулу (φ (θ) = C₁)

.

Таким чином, для малих коливань маятника за допомогою аналізу размерностей і приведених вище додаткових міркувань формула для періоду коливань визначається з точністю до постійного множника. Далі з простого досвіду з використанням годинника або математичного рішення цієї задачі можна отримати значення константи C₁ = 2π. Звичайно, з досвіду отримуємо не 2π, але близьке до нього значення. Отримана формула

.

справедлива для маятників будь-якої довжини l і в будь-якому полі сили тяжіння (на будь-якій планеті).

Приведемо доведення теореми Піфагора. Розглянемо прямокутний трикутник з катетами а і b і гіпотенузою c:

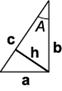
Гострий кут напроти сторони а позначимо A. З міркувань розмірності площа трикутника S пропорційна квадрату однієї із сторін, скажімо, гіпотенузи:

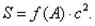
Висота h, опущена з прямого кута на гіпотенузу, розбиває трикутник на два йому подібних, причому їх гіпотенузи рівні а і b відповідно. Гострий кут кожного з цих трикутників рівний A, тому їх площі можуть бути виражені як

Підставляючи ці формули в очевидну рівність S₁ + S₂ = S і скорочуючи на загальний множник f(A), приходимо до шуканої теореми:

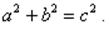
3 Математичні моделі

3.1 Загальна характеристика математичної моделі

У загальному випадку під математичною моделлю об'єкту (системи) розуміється будь-який математичний опис, який відображає з необхідною точністю поведінку реального об'єкту (системи) в реальних умовах. Математична модель відображає записану на мові математики сукупність знань, уявлень і гіпотез дослідника про модельований об'єкт. Оскільки ці знання ніколи не бувають абсалютными, то модель лише приблизно враховує поведінку реального об'єкту.

Математичне моделювання - це засіб вивчення реального об'єкту, процесу або системи шляхом їх заміни математичною моделлю, зручнішою для експериментального дослідження за допомогою ЕОМ.

Математична модель є наближеним представленням реальних об'єктів, процесів або систем, вираженим в математичних термінах і таким, що зберігає істотні риси оригіналу. Математичні моделі в кількісній формі, за допомогою логіко-математичних конструкцій, описують основні властивості об'єкту, процесу або системи, його параметри, внутрішні і зовнішні зв'язки.

У загальному випадку математична модель реального об'єкту, процесу або системи представляється у вигляді системи функціоналів

Ф_i ( X,Y,Z, N, A ,t)=0,

де X - вектор вхідних змінних, X =[x₁,x₂,x₃,..., x_N, t],

Y - вектор вихідних змінних, Y =[y₁,y₂,y₃,..., y_N, t],

Z - вектор стану, Z =[z₁,z₂,z₃,..., z_N, t],

N - вектор зовнішніх дій, N =[n₁,n₂,n₃,..., n_N, t],

A – вектор внутрішніх параметрів, А =[a₁ , a₂ , a₃, …, a_P ],

t - координата часу.

Приклад: Візьмемо деяку просту систему регулювання, структурна схема якої представлена на рис.3.1.

Математичною моделлю системи є диференціальне рівняння:

k₁k₂(x-y) або + k₁k₂y= k₁k₂x

х

k₁

Σ

y

Рис. 3.1 Система регулювання

Характеристики системи: ; Z(t) = [ z₁(t), z₂(t)]; z₁(t) = y(t); z₂ (t)= ; N(t) = 0; A =[k₁, k₂ ].

Функціонування системи полягає в зміні характеристик стану в часі. В деяких випадках характеристики стану можуть визначатися у вигляді явних функцій від параметрів системи, вхідних сигналів, початкових умов і часу. У інших випадках модель є системою рівнянь щодо характеристик станів системи і початкових сигналів. При цьому параметри входять в коефіцієнти рівнянь, а вхідні сигнали – в їх праві частини.

Побудова математичної моделі полягає у визначенні зв'язків між тими або іншими процесами і явищами, створенні математичного апарату, що дозволяє виразити кількісно і якісно зв'язок між тими або іншими процесами і явищами, між фізичними величинами, що цікавлять фахівця, і чинниками, що впливають на кінцевий результат. Зазвичай їх виявляється настільки багато, що ввести в модель всю їх сукупність не вдається. При побудові математичної моделі перед дослідженням виникає завдання виявити і виключити з розгляду чинники, що неістотно впливають на кінцевий результат (математична модель зазвичай включає значно менше число чинників, чим в реальній дійсності). На основі даних експерименту висуваються гіпотези про зв'язок між величинами, що виражають кінцевий результат, і чинниками, введеними в математичну модель. Такий зв'язок часто виражається системами диференціальних рівнянь в приватних похідних (наприклад, в задачах механіки твердого тіла, рідини і газу, теорії фільтрації, теплопровідності, теорії електростатичного і електродинамічного полів).

Форма і принципи представлення математичної моделі залежить від багатьох чинників.

Математичне моделювання, окрім дослідження об'єкту, процесу або системи і складання їх математичного опису, також включає:

· побудова алгоритму, що моделює поведінку об'єкту, процесу або системи;

· перевірка адекватності моделі і об'єкту, процесу або системи на основі обчислювального і натурного експерименту;

· корегування моделі;

· використання моделі.

Побудова математичної моделі зазвичай починається з побудови і аналізу простої, найбільш грубої математичної моделі даного об'єкту, процесу або системи. Надалі, у разі потреби, модель уточнюється, виконується її відповідність об'єкту повнішою.

Візьмемо простій приклад. Потрібно визначити площу поверхні письмового столу. Зазвичай для цього вимірюють його довжину і ширину, а потім перемножують отримані числа. Така елементарна процедура фактично позначає наступне: реальний об'єкт (поверхня столу) замінюється абстрактною математичною моделлю – прямокутником. Прямокутнику приписуються розміри, отримані в результаті вимірювання довжини і ширини поверхні столу, і площа такого прямокутника приблизно береться за шукану площу столу.

Проте модель прямокутника для письмового столу – це проста, найбільш груба модель. При серйознішому підході до завдання перш, ніж скористатися для визначення площі столу моделлю прямокутника, цю модель потрібно перевірити. Перевірки можна здійснити таким чином: зміряти довжини протилежних сторін столу, а також довжини його діагоналей і порівняти їх між собою. Якщо, з необхідним ступенем точності, довжини протилежних сторін і довжини діагоналей попарно рівні між собою, то поверхню столу дійсно можна розглядати як прямокутник. Інакше модель прямокутника доведеться відкинути і замінити моделлю чотирикутника загального вигляду. При вищій вимозі до точності може виникнути необхідність піти в уточненні моделі ще далі, наприклад, врахувати закруглення кутів столу.

Найпростіше будується модель, коли добре відомі закони, що визначають поведінку і властивості об'єкту, процесу або системи, і є великий практичний досвід їх застосування. Складніша ситуація виникає тоді, коли наші знання про об'єкт, що вивчається, процес або систему недостатні. В цьому випадку при побудові математичної моделі доводиться робити додаткові припущення, які носять характер гіпотез, така модель називається гіпотетичною. Виводи, отримані в результаті дослідження такої гіпотетичної моделі, носять умовний характер. Для перевірки виводів необхідно зіставити результати дослідження моделі на ЕОМ з результатами натурного експерименту. Таким чином, питання застосовності деякої математичної моделі до вивчення даного об'єкту, процесу або системи не є математичним питанням і не може бути вирішений математичними методами.

Основним критерієм істинності є експеримент, практика в найширшому сенсі цього слова.

Побудова математичної моделі в прикладних завданнях – один з найбільш складних і відповідальних етапів роботи. Досвід показує, що у багатьох випадках правильно вибрати модель – означає вирішити проблему більш, ніж наполовину. Трудність даного етапу полягає в тому, що він вимагає з'єднання математичних і спеціальних знань. Тому дуже важливо, щоб при вирішенні прикладних завдань математики володіли спеціальними знаннями про об'єкт, а їх партнери, фахівці, – певною математичною культурою, досвідом дослідження в своїй області, знанням ЕОМ і програмування.

Дата добавления: 2014-12-07