Приклад 2. 6 страница

Вбудовані в комп'ютери апаратні генератори випадкових чисел останнім ча­сом часто використовуються в системах захисту інформації. Прикладом застосу­вання таких генераторів для забезпечення конфіденційності, цілісності та досто­вірності електронної інформації, яка зберігається в комп'ютері або передається по мережі, є пристрій для шифрування даних РаdLоск, інтегрований у деякі моделі процесорів, розроблених компанією Іntel. Пристрій має інтерфейс прикладного рівня, що дає змогу розробникам програмного забезпечення отримувати випадкові числа без використання програмних драйверів. Такий спосіб отримання високо­якісних випадкових послідовностей простіший та ефективніший, ніж викори­стання апаратно-програмної RNG (Random Number Generator) архітектури і суто програмних генераторів, що особливо важливо під час побудови захищених і крип­тографічних програм.

Табличний метод. У 1955 році корпорація «Ренд» опублікувала таблиці випадко­вих чисел, які мали мільйон значень. Для заповнення цих таблиць застосовувались апаратні методи. Дані цих таблиць можна використовувати під час моделювання систем за допомогою методу статистичних випробувань. У сучасних комп'ютерах ці таблиці можна зберігати на зовнішніх носіях або навіть в основній пам'яті. Го­ловним недоліком табличного методу є те, що під час його використання витрача­ються значні об'єми основної пам'яті комп'ютера.

Найбільш розповсюдженими на практиці є програмні генератори, які дають змогу отримувати послідовності випадкових чисел за рекурентними формулами. Якщо бути абсолютно точним, то числа, які виробляють програмні генератори, насправді є псевдовипадковими («псевдо» у перекладі з грецької — нібито). Так їх назива­ють тому, що алгоритми їх отримання завжди є детермінованими.

Загалом же програмні генератори повинні задовольняти таким вимогам:

♦ генерувати статистично незалежні випадкові числа, рівномірно розподілені в інтервалі [0, 1];

♦ мати можливість відтворювати задані послідовності випадкових чисел;

♦ затрати ресурсів процесора на роботу генератора повинні бути мінімальними;

♦ легко створювати незалежні послідовності випадкових чисел (потоки).

Слід звернути увагу на те, що більшість програмних генераторів виробляють випадкові числа, рівномірно розподілені в інтервалі [0, 1]. Необхідність моделю­вання таких чисел обумовлена тим, що на їх основі можна отримати випадкові числа практично будь-яких розподілів. Потрібно також мати на увазі, що випадкові числа, які виробляють програмні генератори, є квазірівномірно розподіленими («квазі» у перекладі з латинської — майже). Причина в тому, що вони створюються комп'ю­тером, кількість двійкових розрядів якого обмежена, і за його допомогою можна зобразити тільки дискретні (а не неперервні) значення з діапазону від 0 до 1.

Якість роботи генераторів визначається статистичними властивостями послідов­ностей випадкових чисел, які він виробляє, - незалежністю і випадковістю. Влас­тивості послідовностей перевіряються за статистичними критеріями, детально описаними нижче.

Здатність відтворювання послідовності випадкових чисел полягає в тому, що за однакових початкових умов і параметрів генератор повинен відтворювати одні й ті ж послідовності псевдовипадкових чисел. Ідентичні послідовності випадкових чисел рекомендується використовувати у випадку, коли потрібно порівняти аль­тернативні варіанти систем, що моделюються, і налагодити програми. Однак мож­ливість відтворення не завжди бажана під час моделювання систем і в комп'ю­терних іграх (як це було в перших версіях відомої гри «Тетріс», коли кожна гра починалась з тієї ж послідовності фігур). Для усунення такого недоліку початкові значення величин, необхідних для запуску програмного генератора, рекомендує­ться брати з таймера комп'ютера.

Під час дослідження складних систем виникає необхідність у моделюванні послідовностей випадкових чисел великої довжини. Для їх створення потрібні швидкодіючі алгоритми генерування з мінімальними вимогами до ресурсів ком­п'ютера. Інколи дослідники з невеликим досвідом роботи використовують під час моделювання складних систем один і той же генератор, звертаючись до нього з різ­них місць програми. Однак це часто призводить до того, що процес моделювання швидко вироджується у зв'язку з виходом псевдовипадкової послідовності за ме­жі аперіодичності. Тому для моделювання різних випадкових факторів бажано мати окремі послідовності (набори значень), які відтворювались би одним і тим же генератором, але за різних значень параметрів.

У більшості генераторів псевдовипадкових чисел х_г використовується реку­рентна процедура x_i+1 = f(х_i). Найпростішим та найдавнішим серед таких генера­торів є генератор фон Неймана та Метрополіса, робота якого базувалась на мето­ді середин квадратів. Пояснімо суть цього методу.

Зобразимо умовно довільне чотирирозрядне десяткове число як х х х х. Підне­семо це число до квадрату і в отриманому результаті відкинемо по дві цифри злі­ва і справа:

Чотири цифри, які залишились, і є новим випадковим числом. Якщо результа­том множення є число з кількістю цифр менше восьми, зліва дописуються додат­кові нулі. Реалізувати програмно цей генератор дуже просто, але він має ряд вад:

♦ якщо початкове число парне, то може відбутися виродження послідовно­сті, тобто починаючи з деякого значення всі наступні дорівнюватимуть нулю (спробуйте взяти як початкове число 4500);

♦ числа, які виробляє генератор, є сильно корельованими.

6.2.2. Лінійні конгруентні генератори

Зважаючи на ці вади, на практиці використовують більш складні програмні гене­ратори. У більшості сучасних програмних генераторів використовується властивість конгруентності, яка полягає в тому, що два цілих числа А і В є конгруентними за модулем т, якщо їх різниця (А - В) є числом, яке ділиться на т без остачі (тобто є кратним m). Записується це так:

Наприклад, щоб знайти число, конгруентне з числом 134 за модулем 10, необ­хідно знайти цілочислову остачу від ділення 134 на 10, яка дорівнює 4.

Наведемо кілька прикладів обчислення конгруентних значень для різних т:

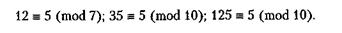
Серед методів генерування випадкових чисел найбільш поширеним є ліній­ний мультиплікативний конгруентний метод:

(6.1)

Однією із вад лінійних конгруентних генераторів є те, що де і = 1, 2,...; а, с і т — цілі константи. Щоб отримати нове число, необхідно взяти псевдовипадкове число x_i (або задати вихідне х₀), помножити його на коефіцієнт а, додати константу с і взяти модуль отриманого числа за т, тобто розділити на т, і отримати остачу. Ця остача і буде наступним псевдовипадковим числом х_і+1. У разі правильного підбору параметрів цей генератор повертає випадкові числа від 0 до т - 1.

Отримані за формулою (6.1) значення х_і+1 належать до діапазону 0 < х_і+1 < т - 1 і мають рівномірний дискретний розподіл. Для того щоб отримати випадкове значення r _і+1 з інтервалу [0, 1], необхідно число x_i+1 розділити на т. У цьому разі всі значення т, с, а, x₀ повинні бути додатними й задовольняти умовам: 0 < т; а < т; с < т; х₀< т. Отримана за формулою (6.1) послідовність називається ліній­ною конгруентною послідовністю.

Однією із вад лінійних конгруентних генераторів є те, що отримані випадкові числа х_i+1 суттєво залежать від значень т, с, а, х₀ і обчислюються за однією й тією ж формулою (6.1), тобто не є абсолютно випадковими. Але незважаючи на те що алгоритм їх отримання є детермінованим, за умови відповідного вибору констант т, с, а послідовність чисел х_і+1 на основі яких отримують значення r_і+1, повністю задовольнятиме більшості статистичних критеріїв.

Ще одна вада цих генераторів стосується того, що випадкові числа r_i+1, отрима­ні за допомогою генератора, можуть приймати тільки дробово-раціональні значен­ня - 0; І/m; 2/m;...; (m-1)/m. Більше того, числа r_і+1 можуть приймати лише деякі з указаних значень залежно від вибраних параметрів т, с, а і х₀, а також від того, як реалізується операція ділення чисел з плаваючою комою на число т у комп'ютері, тобто залежно від типу комп'ютера і системи програмування. Наприклад, якщо т = 10, х₀ = а = с = 7, то отримаємо послідовність 7; 6; 9; 0; 7; 6; 9; 0,..., яка не є випадко­вою. Це свідчить про важливість правильного вибору значень констант т, с, а і х₀ Правильно підібрані значення іноді називають магічними числами.

Наведений приклад ілюструє й те, що конгруентна послідовність завжди є ци­клічною, тобто вона починає повторюватися через певну кількість випадкових чи­сел. Кількість значень, після яких випадкові числа починають повторюватися, на­зивається повним періодом генератора і є основним його параметром. Значення повного періоду залежать від розрядності комп'ютера, а також від значень т,с,а і х₀. Існує теорема, яка визначає умови існування повного періоду генератора, а саме:

♦ числа с і т повинні бути взаємно простими, тобто мати взаємний дільник 1;

♦ значення b = а - 1 має бути кратним q для кожного простого q, бути діль­ником т;

♦ значення b має бути кратним 4, якщо т кратне 4.

Достатність цих умов уперше було доведено Халлом (Нull) і Добеллом (Dobell).

Якщо с > 0, то генератор називається мішаним, а якщо с = 0 — мультиплікативним.

Розглянемо, як потрібно вибирати параметри лінійного конгруентного генера­тора, щоб отримати послідовність з повним періодом. Для отримання такої послі­довності необхідно вибирати значення т = 2^g -1, де g — довжина розрядної сітки комп'ютера. Для 32- розрядного комп'ютера т — найбільше ціле число, яке може бути відтворене в ньому, дане число дорівнює 2³¹ - 1 = 2147483647 (один розряд відводиться під знак числа). У цьому разі ділення х_i+1/т виконувати не обов'яз­ково. Якщо в результаті роботи генератора буде отримане число х_і+1, яке більше ніж те, що може бути відтворене в комп'ютері, виникне переповнення розрядної сітки. Це призведе до втрати крайніх лівих двійкових знаків цілого числа, які пе­ревищили допустимий розмір. Однак розряди, що залишились, саме і є значення­ми x_i+1 (mod 2^g). Таким чином, під час генерування замість операції ділення мож­на скористатись переповненням розрядної сітки.

Стосовно константи с теорема стверджує, що для отримання послідовності з повним періодом генератора значення с повинне бути непарним, і, крім того, c - 1 має ділитися на 4. Для такого генератора початкове значення х₀ може бути до­вільним і лежати в діапазоні від 0 до т - 1. Якщо с = 0, то отримуємо мультиплікативний конгруентний метод, який передбачає використання таких рекурент­них виразів:

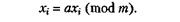(6.2)

Цей метод більш швидкодіючий, ніж попередній, але він не дає послідовності з повним періодом. Дійсно, з виразу (6.2) видно, що значення х_і+1 = 0 може з'яви­тись тільки в тому випадку, якщо послідовність вироджується в нуль. Таким чином, якщо с = 0, потрібно, щоб x_i і т були взаємно простими числами з т і знаходились між 0 і т.

Що стосується вибору а, то у випадку, коли т = 2^g, де g > 4, є єдина вимога стосовно значення а:

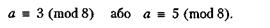
У цьому випадку четверта частина всіх можливих значень множників дає дов­жину періоду, що дорівнює m/4, яка й буде максимальним періодом генератора.

Існують й інші конгруентні методи генерування випадкових чисел, серед яких слід відзначити адитивний.

Найпростіший генератор, послідовність якого х_і+1 залежить більше ніж від од­ного з попередніх значень, — це генератор, що використовує числа Фібоначчі:

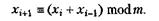
Цей генератор широко використовувався в 50-ті роки XX століття, але, як пока­зали подальші дослідження, статистичні властивості його досить низькі. Більш складні методи генерування випадкових чисел можна знайти в праці.

Розглянуті методи генерування випадкових чисел не стосують­ся дослідників, які використовують мови або пакети моделювання. Ці засоби містять вбудовані генератори випадкових чисел, якість яких залежить від розроб­ників цих програмних засобів. На жаль, є ще багато пакетів моделювання, в яких застосовуються генератори досить низької якості. Що стосується мов про­грамування загального призначення, то засоби генерування випадкових чисел, вбудовані в них, взагалі не задовольняють будь-яким статистичним критеріям. Тому їх не слід використовувати під час проведення відповідальних досліджень.

6.3 Моделювання випадкових подій та дискретних величин

У разі дослідження складних систем методом статистичних випробувань необхідно мати можливість отримувати за допомогою комп'ютера вибіркові значення випад­кових величин, які мають різні закони розподілу. Випадкові величини зазвичай моделюють за допомогою перетворення одного або кількох незалежних значень випадкової величини R, рівномірно розподіленої в інтервалі [0, 1], що познача­ються як r_i, і =1, 2, 3,... (r_i є [0,1]). Значення r_i, генерують, як звичайно, за допомо­гою програмних генераторів випадкових чисел.

6.3.1. Незалежні випадкові події

Припустимо, що ймовірність настання деякої елементарної випадкової події А в од­ному випробуванні дорівнює Р(A) = р. Вважається, що умови проведення кожно­го вигробування однакові і його можна повторити нескінченну кількість разів. Якщо r_i, - це значення рівномірно розподіленої в інтервалі [0, 1] величини, то можна стверджувати, що за умови r_i ≤ р (рис. 6.1) настане подія А, а якщо r_i > р, то подія A не відбудеться.

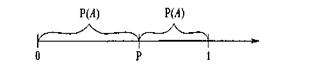
Рис. 6.1. Моделювання настання випадкових подій

Дійсно, якщо f(r) - функція щільності рівномірно розподіленої випадкової величини r, то

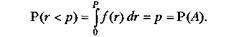
Ця модель добре описує такі події, як обслуговування вимоги в пристрої СМО, що може бути вільним або зайнятим, успішну або ні спробу виконання деякого завдання, влучення або ні в ціль, розгалуження потоків інформації у двох і більше напрямках. У деяких мовах для моделювання випадкової події використовується спеціальний блок (наприклад, у мові СРSS — блок TRANSFER, який працює в стати­стичному режимі).

6.3.2. Група несумісних подій

Нехай є група несумісних подій А₁, А₂,..., А_k настання яких необхідно дослідити.

Відомі ймовірності настання цих подій р₁ = Р (A₁), р₂ = Р(А₂), p₃ = Р(Aз), …,

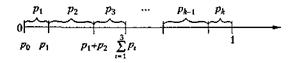
p_k = P (A_k). Якщо події несумісні, то ∑ p_i = 1. Припустимо, що р₀ = 0. На відріз­ку [0, 1] числової осі відкладемо значення цих імовірностей (рис. 6.2).

Рис. 6.2. Моделювання групи несумісних подій

Якщо отримане від генератора випадкових чисел значення r_i, потрапляє в інтервал від ∑ p_{к ,} к = 0,1,2,….(і-1) до ∑ p_{к ,} к = 0,1,2,… і, вважаємо, що відбулася подія А_i. Таку процедуру називають визначенням результату випробування за жеребом. Вона грунтується на формулі

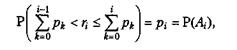
де р₀ = 0.

Ця модель часто використовується в теорії прийняття рішень і добре відтворює процеси вибору однієї з багатьох альтернатив у комп'ютерних іграх, розгалужен­ня потоків інформації у вузлах мережі в кількох напрямках, вибір одного з бага­тьох пристроїв для обслуговування в СМО і т. ін.

6.3.3. Умовна подія

Умовна подія А - це подія, яка відбувається з імовірністю Р(А/В) тільки за умо­ви, що настала подія В (рис. 6.3). У цьому разі має бути задана ймовірність Р(В) настання події В. Моделювання настання умовної події А провадиться таким чи­ном. Спочатку випадкове число r_i отримане від генератора випадкових чисел, використовується для моделювання настання події В. Подія В настає в тому випад­ку, якщо справджується нерівність r₁ ≤ Р(В). Настання події А моделюється за допомогою числа r₂. Для цього перевіряється умова r₂ ≤ Р(А), за виконання якої приймається рішення, що подія А відбулася. Якщо ж подія В не відбулася, то настання події А моделювати не потрібно. Таким чином, мож­на скоротити загальну кількість випробувань.

Рис. 6.3. Моделювання настання умовної події

6.4 Моделювання безперервних випадкових величин

Існує кілька методів моделювання значень безперервних випадкових величин з до­вільним законом розподілу на основі випадкових чисел, рівномірно розподілених у інтервалі [0, 1]: метод оберненої функції, метод відсіювання, наближені мето­ди тощо.

6.4.1. Метод оберненої функції

Розглянемо метод моделювання випадкової величини, яка має функцію щіль­ності ймовірностей f(x) і монотонно зростаючу функцію розподілу F(х) (рис. 6.4). Суть методу така. За допомогою генератора випадкових чисел генеруємо зна­чення випадкової величини r_{i ,} якому відповідає точка на осі ординат. Значення випадкової величини х_i з функцією розподілу F(х) можемо одержати з рівняння F(x_i) = r_i.

Дійсно, якщо на осі ординат відкласти значення r_i випадкової величини, розпо­діленої рівномірно в інтервалі [0, 1], і на осі абсцис знайти значення х_i випадкової величини (рис. 6.4), при якому F(х_i) = r_i, то випадкова величина X = F^-1 (r) буде мати функцію розподілу F(х). За визначенням функція розподілу F(х) випадко­вої величини X дорівнює ймовірності Р(Х < х):

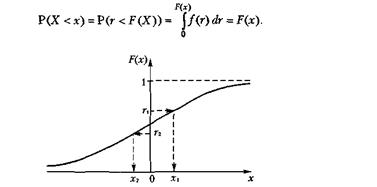
Рис. 6.4. Використання методу оберненої функції для генерування неперервної випадкової величини

Таким чином, послідовність випадкових чисел r₁, r₂, r₃,... перетворюється на послідовність x₁, х₂, x₃,..., яка має задану функцію щільності розподілу f(х). Звід­си випливaє загальний алгоритм моделювання випадкових неперервних величин, що мають задану функцію розподілу ймовірностей:

♦ генерується випадкове число r_i є [0, 1];

♦ обчислюється випадкове число х_i, яке є розв'язком рівняння

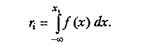
Приклади застосування методу наведені нижче.

6.4.2. Рівномірний розподіл

У загальному випадку випадкова величина X є рівномірно розподіленою на від­різку [а, b], якщо її щільність розподілу ймовірностей має вигляд

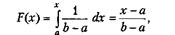
Функцію розподілу ймовірностей можна знайти як

тобто

Графіки функцій щільності f(x) та ймовірності F(х) зображено на рис. 6.5.

Рис. 6. 5. Функції щільності (а) і розподілу (б) рівномірно розподіленої випадкової' величини

Математичне сподівання та дисперсія випадкової величини X визначаються як

Для моделювання випадкової рівномірно розподіленої на відрізку [а, b] вели­чини можна скористатись методом оберненої функції. Обчислимо функцію роз­поділу випадкової величини та прирівняємо її до значення r_i:

Звідси знаходимо значення випадкової величини з функцією розподілу f(х):

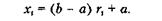
Цю формулу також можна отримати, якщо виконати лінійне перетворення ін­тервалу [0,1] у відрізок [а, b]. Для цього потрібно змінити масштаб функції рівно­мірного розподілу, помноживши її на (b - а), а потім змістити її на величину а.

6.4.3. Експоненціальний розподіл

Експоненціальний закон розподілу набув широкого використання в теорії надій­ності

Для її моделювання скористаємося методом оберненої функції. Маємо

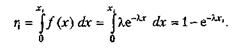
З попереднього виразу знаходимо значення х_i

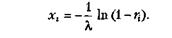
Можна показати, що випадкові величини (1 - r_i) мають такий самий розподіл, що і величини r_i,. Тоді, замінивши 1 - r_i, на r_i отримаємо

Випадкові величини з експоненціальним розподілом широко застосовуються в задачах моделювання та аналізу СМО, наприклад під час моделювання проце­сів виходу з ладу та ремонту обладнання, які виникають у складних системах, у разі визначення інтервалів часу між послідовними викликами абонентів у теле­фонній мережі або замовлень від незалежних клієнтів у будь-якій мережі обслу­говування (швидка допомога, служби ремонту, виклик таксі і т. ін.)

6.5 Моделювання випадкових процесів

Випадковий процес — це процес (тобто зміна в часі стану деякої системи чи об'єк­та), який розвивається під впливом якихось випадкових чинників і для якого зада­но ймовірнісні характеристики його протікання. До числа таких процесів можна віднести багато виробничих процесів, які супроводжуються випадковими флук­туаціями, а також процесів, з якими можна зустрітись у природничих науках, економіці, соціології тощо.

Моделювання будь-якого процесу, в тому числі і випадкового, полягає у від­творенні значень (величин) реалізації цього процесу. Випадковий стаціонарний процес задається значеннями математичного сподівання та автоковаріаційною або автокореляційною функцією. Для його моделювання скористаємось парамет­ричними моделями авторегресії, які широко застосовуються для аналізу часових рядів.

Авторегресійний процес к-го порядку з постійними коефіцієнтами визнача­ється рівнянням регресії

Значення процесу у будь-який момент часу t визначається через попе­редні значення та випадкове збурення e_t. На практиці звичайно використовують авторегресійні моделі процесів першого і другого порядку (процес Маркова і Юла-Уокера), автокореляційна функція яких є згасаючою (рис. 6.6).

Рис. 6.6. Автокореляційна функція стаціонарного процесу

Параметри процесу a₁, a₂, …, a_k визначаються через коефіцієнти автокореляції. Так, для процесу Юла

де ρ₁, ρ₂ — значення автокореляційної функції при зсувах 1 та 2.

Під час побудови рівняння авторегресії висуваються дві гіпотези. Перша — про стаціонарність процесу, друга — про те, що збудження е_t є випадковим проце­сом у широкому розумінні слова з нормальною функцією розподілу, нульовим математичним сподіванням і дисперсією σ². На рис. 6.7, а зображено графік ви­падкового процесу і нормальний розподіл збурення е_t (рис 6.7, б).

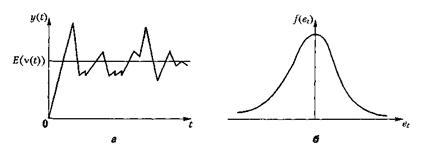
Рис. 6.7 Графіки випадкового процесу (а) і нормального розподілу збурення (б)

Процес у_t називається марківським, якщо для будь-яких моментів часу

t₁ <t₂<t₃<... <t_n, умовна ймовірність значення y_t залежатиме від у_t-1 і не залежатиме від того, в якому стані процес знаходився в попередні моменти часу. Під час моделювання марківського стаціонарного процесу з параметрами М [у_t], ρ₁, σ² діють таким чином. За початковий член ряду можна взяти будь-яке значення ви­падкового процесу (тому що будь-яка частина стаціонарного процесу є повноцін­ним представником усього процесу і має ті ж імовірнісні характеристики), на­приклад у_t-1 = 0 або y_t-1 = М [ у_t]. За допомогою рівняння регресії розраховуємо значення у_t+1 при заданих а₀ = М [ y_t ] і a₁ = ρ₁ без урахування збурення е_t і моделюємо значення нормально розподіленої випадкової величини з математичним сподіванням, що дорівнює нулю, і дисперсією σ². Отримане значення додаємо до у_t-1 і таким чи­ном отримуємо нове значення реалізації випадкового процесу. Повторюємо про­цедуру для обчислення інших значень за рівнянням регресії, задаючи як початкове значення у_t тобто моделюємо у_t+1,..., у_t+k. Така методика дає змогу моделювати випадкові стаціонарні процеси з будь-якими автокореляційними та багатомірними функціями розподілів.

7 Прийняття рішень за результатами моделювання.

Заключний етап експериментів з імітаційними моделями — це прийняття рі­шень щодо визначення оптимальних параметрів системи або удосконалення її структури, тому результати моделювання важливо подавати у зручному для ана­лізу і зрозумілому для замовника чи аналітика вигляді. Вибір методів прийняття рішень за результатами імітаційного моделювання суттєво залежить від мети до­сліджень. Це можуть бути як складні методи оптимізації, так і методи простого перебору чи вибору одного із кількох варіантів.

7.1 Відображення результатів моделювання

Імітаційне моделювання завжди використовується для прийняття рішень щодо модельованої системи, але перш ніж представляти результати моделювання ана­літику, їх потрібно перетворити таким чином, щоб вони мали наочний та інфор­мативний вигляд. Більшість програмних засобів імітаційного моделювання відо­бражають результати моделювання у формі стандартного звіту, в якому зібрані статистичні дані, що стосуються характеристик системи, наприклад завантаже­ності ресурсів, довжини черг, часу перебування вимог у чергах і пристроях, а та­кож гістограми розподілів вихідних величин та ін. Крім стандартних статистич­них даних користувач може включити у звіт необхідні йому дані й надрукувати їх у потрібному для нього вигляді.

Дата добавления: 2014-12-07