Правило Лопиталя

Дифференциал функции

Производная сложной функции

Если переменная у — функция от переменной и, т. е. y = f (и), а переменная и = 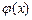— функция от переменной х, то говорят, что задана сложная функция у = .

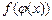Теорема. Если функции y = f (и), и = 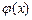дифференцируемы, то производная сложной функции существует и может быть вычислена по формуле .

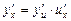Таблица производных

1. (uⁿ) ' = n · u^{n – 1} · u', (n 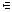R).

2. .

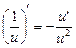3. .

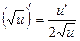4. .

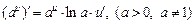5. (e^u) ' = e^u · u'.

6. .

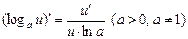7. (ln u) ' = .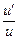

8. (sin u) ' = cos u · u'.

9. (cos u) ' = –sin u · u'.

10. (tg u) ' = .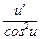

11. (ctg u) ' = .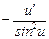

12. (arcsin u) ' = .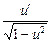

13. (arccos u) ' = .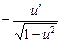

14. (arctg u) ' = .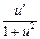

15. (arcctg u) ' = – .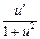

Дифференциалом функции y = f (х) в точке х ₀ называется глав-
ная линейная относительно 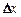часть приращения функции в этой точке х ₀, т. е. dy = A · .

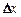Число А равно производной функции y = f (х) в точке х ₀, т. е.

А = f' ( x ₀).

Дифференциал dy функции в произвольной точке х равен произведению f' (x) на дифференциал dх переменной х, т. е.

dy = f' ( x ) dx.

Теорема. Пусть функции f ₁(x) и f ₂(x) определены и дифференцируемы в некоторой окрестности точки х ₀, за исключением, быть может, самой точки х ₀. Кроме того, пусть также =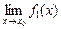
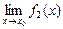= = 0 или 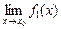= 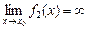, причем 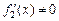в указанной окрестности точки х ₀.

Тогда, если существует предел отношения 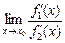(конечный или бесконечный), существует и предел 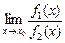, причем справедлива формула = .

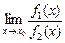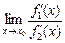Замечание 1. При необходимости правило Лопиталя может быть применено два и более раз.

Замечание 2. Теорема остается верной и в случае, когда ().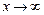

Пример. 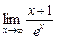= = = = 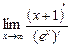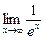0.

Схема исследования функции

При исследовании функций и построении графиков рекомендуется использовать нижеприведенную схему.

1. Указать область определения функции D (y).

2. Исследовать функцию на четность, нечетность.

Функция y = f (x) с симметричной относительно начала координат областью определения D (y) называется четной, если для всех х 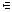D (y) выполняется равенство f (– x) = f (x), и нечетной, если f (– x) = –f (x). График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.

3. Провести исследование функции на периодичность.

Если функция периодическая, то дальнейшее исследование можно проводить на интервале, длина которого равна периоду.

4. Исследовать поведение функции на границе области опре-
деления, найти односторонние пределы в точках разрыва. Найти асимптоты.

Прямая 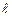называется асимптотой графика функции y = f (x), если расстояние от точки М графика функции до прямой 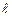стремится к нулю при неограниченном удалении этой точки по графику функции от начала координат. Различают вертикальные, наклонные и горизонтальные асимптоты.

Пусть х ₀ — точка разрыва функции. Прямая х = х ₀ называется вертикальной асимптотой графика функции y = f (x), если хотя бы один из односторонних ее пределов в точке х ₀ равен 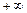(или ).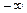

Если существуют и конечны 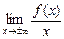= k, 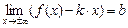, то прямая у = k · x + b называется наклонной асимптотой графика функции y = f (x).

Горизонтальная асимптота — это частный случай наклонной
при k = 0.

5. Найти производную y'.

6. Найти критические точки функции, т. е. те значения аргумента х, которые принадлежат D (y) и в которых производная y' равна нулю или ее не существует.

7. Найти интервалы монотонности и точки локальных экстремумов.

Теорема 1. Если дифференцируемая функция y = f (x), х 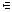(a, b) возрастает (убывает) на интервале (a, b), то 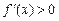(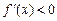) для любого х 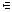(a, b).

Теорема 2. Если функция y = f (x), х 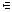(a, b) имеет положительную (отрицательную) производную в каждой точке интервала (a, b), то эта функция возрастает (убывает) на интервале (a, b).

Точка х ₀, принадлежащая D (y), называется точкой локального минимума (максимума) функции y = f (x), если найдется такая 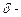окрест-
ность (х ₀ – 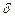; х ₀ + 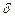) 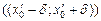точки х ₀ (х' ₀), что для всех
х 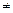х ₀ (х 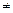х' ₀) из этой окрестности (рис. 12) выполняется неравенство

.

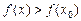
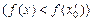Точки локальных минимума и максимума называются точками локального экстремума, а значения функции в этих точках называются локальными экстремумами функции.

Теорема 3. Пусть функция y = f (x) непрерывна в критической точке х ₀ и в некоторой 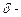окрестности имеет конечную производную, кроме, быть может, самой точки х ₀. Если при переходе через точку х ₀ производная f' (x) меняет свой знак с плюса на минус, то х ₀ является точкой локального максимума, если же f' (x) при переходе через х ₀ меняет знак с минуса на плюс, то она является точкой локального минимума.

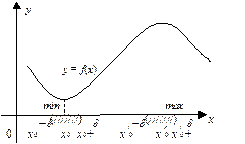
Рис. 12

8. Найти вторую производную 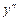, т. е. производную от первой производной .

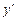9. Определить интервалы выпуклости, вогнутости графика функции, точки перегиба.

График функции y = f (x) имеет на интервале (a, b) выпуклость (вогнутость), если он расположен ниже (выше) любой касательной, проведенной к нему в любой точке из (a, b) (рис. 13).

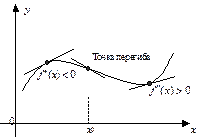
Рис. 13

Точка графика функции из D (y), в которой выпуклость сменяется вогнутостью (или наоборот), называется точкой перегиба.

Теорема. Если во всех точках интервала (a, b) функция y = f (x) имеет отрицательную (положительную) вторую производную 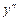, то график этой функции на интервале (a, b) является выпуклым (вогнутым). Если вторая производная 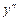при переходе через точку х ₀, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х ₀ — точка перегиба.

10. Найти точки пересечения графика с осями координат, интервалы знакопостоянства фукции (промежутки, на которых f (x) > 0 или f (x) < 0), контрольные точки.

11. Построить график функции с учетом проведенного исследования.

Дата добавления: 2014-12-08