Равномерный и нормальный законы распределения непрерывных случайных величин

Числовые характеристики непрерывной случайной величины

1. Математическое ожидание

Математическое ожидание непрерывной случайной величины Х:

.

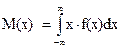(5.11)

f(х) – плотность вероятности распределения случайной величины Х.

1. Дисперсия

Дисперсия непрерывной случайной величины Х:

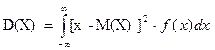	.	(5.12)
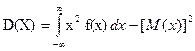	.	(5.13)

1. Среднее квадратическое отклонение определяется формулой (5.2).

На практике приходится при решении задач сталкиваться с различными распределениями непрерывных случайных величин. Плотность распределения f(x) непрерывной случайной величины называют законом распределения.

Следует рассмотреть некоторые важные для практики распределения случайных величин и соответствующие им числовые характеристики.

1. Равномерный закон распределения вероятностей

Непрерывная случайная величина X называется распределенной равномерно на отрезке [a,b], если её плотность распределения вероятностей постоянна на данном отрезке:

.

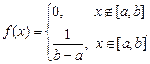(5.14)

Функция распределения в этом случае согласно (5.7), примет вид:

.

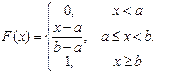(5.15)

Числовые характеристики случайной величины X равномерно распределенной на интервале [a,b]:

1. Математическое ожидание по формуле (5.11):

.

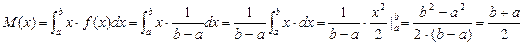2. Дисперсия по формуле (5.13):

.

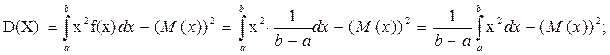
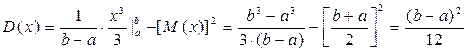3. Среднее квадратическое отклонение – s(Х) по формуле (5.2):

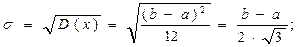
Пример 4.

Найти дисперсию и среднее квадратическое отклонение случайной величины X, равномерно распределенной на интервале (2;6).

Решение.

Математическое ожидание:

.

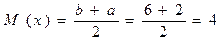Дисперсия:

.

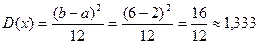Среднее квадратическое отклонение:

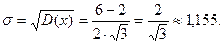
Это распределение реализуется, например, в экспериментах, в которых наудачу ставится точка на интервале [a,b], при этом случайная величина X – абсцисса поставленной точки.

Вероятность попадания равномерно распределенной непрерывной случайной величины Х на интервале [a,b], определяется по формуле (5.9а).

Примером равномерно распределенной непрерывной случайной величины Х является ошибка при округлении отсчета до ближайшего целого деления шкалы измерительного прибора, проградуированной в некоторых единицах.

Пример 5.

Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего деления. Найти вероятность того, что ошибка отсчета: а) превысит значение 0,04; б) меньше 0,04.

Решение.

Ошибку округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними делениями. Плотность равномерного распределения по формуле (5.14) равна:

,

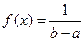где (b – a) – длина интервала, в котором заключены возможные значения Х.

Вне этого интервала f (x) = 0. В рассматриваемой задаче длина интервала, в котором заключены возможные значения Х, равна 0,2. Поэтому плотность распределения вероятностей равна:

.

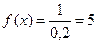Тогда ошибка отсчета превысит значение 0,04, если она будет заключена в интервале (0,04; 0,2). По формуле (5.9а) вычисляется вероятность того, что при отсчете будет сделана ошибка превышающая значение 0,04:

.

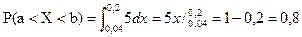Ошибка отсчета меньше 0,04 будет заключена в интервале (0; 0,04) с вероятностью:

.

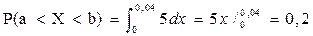На рис. 5.3 представлен график функции р(х) случайной величины, равномерно распределенной на промежутке [a;b].

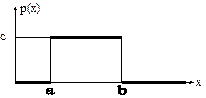
Рис. 5.3. Плотность распределения вероятностей случайной величины, равномерно распределённой на отрезке [a;b]

1. Нормальный закон распределения вероятностей

Непрерывная случайная величина x имеет нормальльное распределение с параметрами: m,s > 0, если плотность распределения вероятностей имеет вид:

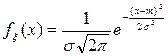
(5.16)

где: m – математическое ожидание, s– среднеквадратическое отклонение.

Нормальное распределение называют еще гауссовским по имени немецкого математика Гаусса [1777-1855]. Тот факт, что случайная величина имеет нормальное распределение с параметрами: m, 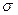, обозначают так: N (m,s), где: m=a=M[X];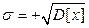

Достаточно часто в формулах математическое ожидание обозначают через а. Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:

.

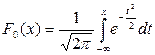(5.17)

График плотности нормального распределения, который называют нормальной кривой или кривой Гаусса, изображен на рис.5.4.

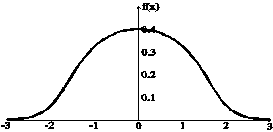
Рис. 5.4. Плотность нормального распределения

Определение числовых характеристик случайной величины по её плотности рассматривается на примере.

Пример 6.

Непрерывная случайная величина задана плотностью распределения: .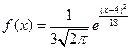

Определить вид распределения, найти математическое ожидание M(X) и дисперсию D(X).

Решение.

Сравнивая заданную плотность распределения с (5.16) можно сделать вывод, что задан нормальный закон распределения с m =4. Следовательно, математическое ожидание M(X)=4, дисперсия D(X)=9.

Среднее квадратическое отклонение s=3.

Функция Лапласа, имеющая вид:

,

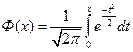(5.17а)

связана с функцией нормального распределения (5.17), cоотношением:

F₀(x) = Ф(х) + 0,5.

Функции Лапласа нечётная.

Ф(-x)=-Ф(x).

Значения функции Лапласа Ф(х) табулированы и берутся из таблицы по значению х (см. Приложение 1).

Нормальное распределение непрерывной случайной величины играет важную роль в теории вероятностей и при описании реальности, имеет очень широкое распространение в случайных явлениях природы. На практике очень часто встречаются случайные величины, образующиеся именно в результате суммирования многих случайных слагаемых. В частности, анализ ошибок измерения показывает, что они являются суммой разного рода ошибок. Практика показывает, что распределение вероятностей ошибок измерения близко к нормальному закону.

С помощью функции Лапласа можно решать задачи вычисления вероятности попадания в заданный интервал и заданного отклонения нормальной случайной величины.

Дата добавления: 2014-12-27