Проверка нормальности распределения

Соответствие экспериментального распределения нормальному проверяется следующими способами:

1. По числам Вестергарда при нормальном распределении в пределах:

х ± 0.3 σ находится 25 % всех единиц наблюдения;

х ± 0.7 σ находится 50 % всех единиц наблюдения;

х ± l,l σ находится 75 % всех единиц наблюдения;

х ± 3,0 σ находится 99 % всех единиц наблюдения.

2. По соотношению средней арифметической и структурных средних:

- при нормальном распределении, которое обладает симметричностью:

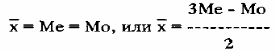
- правило "двух третей" Юла:

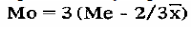
а) если распределение симметрично: Me = Mo;

б) если распределение обладает правосторонней асимметрией: Me > Mo;

в) если распределение имеет левостороннюю асимметрией Me < Mo

3. По коэффициенту асимметрии (skewness):

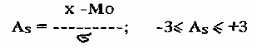
а) если распределение симметрично: A s = 0

б) при правосторонней асимметрии: A s > 0

в) при левосторонней асимметрии: A s < 0

4. Если Ме занимает срединное положение между 25-м и 75-м процентилем, то распределение близко к нормальному.

Графическое изображение симметричного и асимметричного распределений:

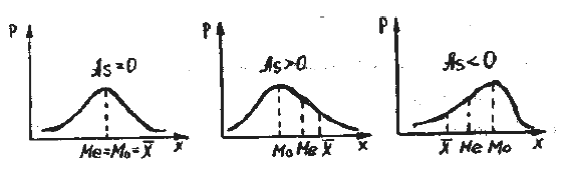
Так как значительная часть статистических методов (параметрическая статистика) основана на предположении, что распределение близко к нормальному, то, если экспериментальные данные не ложатся на кривую нормального распределения, их пытаются преобразовать таким образом, чтобы полученная кривая соответствовала нормальному распределению. Наиболее часто используются следующие способы "нормализацующего преобразования" (transformation to normality) данных:

􀂃 гармоническое преобразование: 1 /х;

􀂃 извлечение квадратного корня: i x

􀂃 логарифмирование {дает наиболее точное приближение}: log xi

Успешность преобразования данных оценивают по коэффициенту асимметрии: чем ближе

он к 0, тем ближе экспериментальное распределение к нормальному.

Исключение "выскакивающих" вариант.__

Иногда в небольших совокупностях встречаются варианты резко отличающиеся по своему значению от других, так называемая «выскакивающая» варианта (outlying case). Если данное отличие обусловлено случайными колебаниями изучаемой величины, то такие варианты оставляют в совокупности и включают в общее число наблюдений. Если отличие обусловлено ошибками в исследовании или ее причину точно нельзя установить, то "выскакивающие" варианты необходимо исключить из исследования. Методика исключения вариант:

- рассчитываются средняя величина и стандартное отклонение без учета "выскакивающих" вариант;

- анализируется соотношение:

- если Хвыск - х, > σ * f, то "выскакивающая" варианта исключается из исследования;

- если ХВЫСК - х < σ * f то "выскакивающая" варианта должна быть оставлена в общем числе наблюдений.

При этом f - коэффицент Романовского, который определяется по специальной таблице с учетом числа наблюдений и вероятностью исключения варианты.

Задание для самостоятельной работы по средним величинам и

мерам рассеяния:

1. Сформируйте вариационный ряд из предложенных данных.

2. Вычислите среднюю величину, стандартное отклонение, моду, медиану, коэффициент вариации (оцените его).

3. Можно ли считать, что предложенный для анализа признак имеет нормальное распределение?

Задача – эталон

Приведены результаты измерения частоты пульса у некурящих студентов-медиков в возрасте 20 лет:

68,58,65,55,70,62,60,65,70,58,62,58,62,60,60,65,62,55,62,58,60,70,62,65,60,68,65,62,68, 65,60,62,60,68,65,60,62,60,65,62,68

Построим вариационный ряд:

Графическое изображение распределения результатов измерения частоты пульса у студентов-медиков

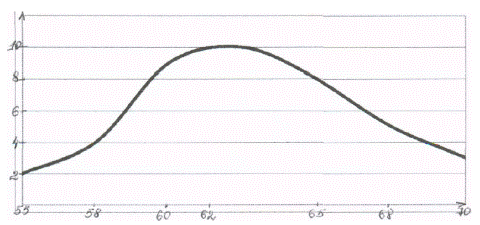
Средняя величина –средняя частота пульса у некурящих студентов-медиков

X= 2x55 + 4x58 + 9x60 + 10x62+ 8x65+ 5x68 + 3x70 / 41 -2572 / 41 = 62,73 ударов в минуту

М0 = 62 удара в минуту

Ме = 62 удара в минуту

Стандартное отклонение 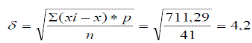уд.в минуту

Коэффициент вариации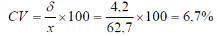

Проверка нормальности распределения

Коэффициент асимметрии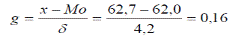

Вывод: Так как коэффициент асимметрии близок к 0, можно предположить нормальное

распределения. Тогда центральная тенденция оценивается по средней величине, х=62.7

уд.в минуту (частота пульса у некурящих студентов-медиков), а разброс характеризует

стандартное отклонение δ = 4,2 уд. в минуту. Так как коэффициент вариации СV < 10%

(СV=6,7), то изучаемую совокупность можно считать однородной.

Контрольные вопросы:

1. Приведите примеры использования в здравоохранении абсолютных чисел для анализа явлений и процессов.

2. Почему при анализе результатов исследования возникает потребность в обобщении полученных данных и каковы основные виды этого обобщения?

3. Назовите виды относительных величин и приведите примеры их использования в анализе общественного здоровья.

4. Назовите виды средних величин, условия их использования и приведите примеры их практического применения.

5. Что такое вид распределения случайной величины и какие виды распределения знаете (примеры)?

6. Проведите сравнительный анализ параметрической и непараметрической статистики.

7. Для чего необходимо формирование вариационного ряда и каковы его правила?

8. Покажите на примерах виды вариационных рядов.

9. Расскажите об основных направлениях анализа вариационного ряда.

10. Какие характеристики относятся к показателям центральной тенденции ряда и каково их практическое применение?

11. Что такое «меры рассеяния» и какие показатели к ним относятся?

12. Опишите достоинства и недостатки критериев разнообразия вариационного ряда.

13. В чем заключается правило «трех сигм» на конкретных примерах здравоохранения?

14. Как проверить нормальность распределения?

15. В чем заключается правило исключения «выскакивающих» вариант?

Дата добавления: 2014-12-23