Если округлить результат до двух знаков, то

Решение тренировочных заданий.

Задание I.

Представим суммарную погрешность 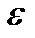в виде суммы трех слагаемых.

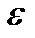=0,01=0,009+0,0005+0,0005.

Выберем h из условия

.

Так как 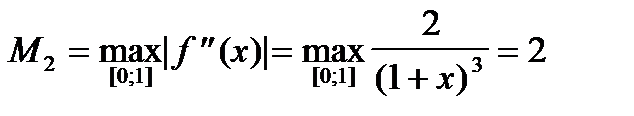и (b-a)=1, то 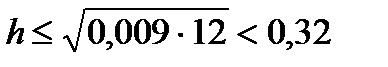и, следовательно, 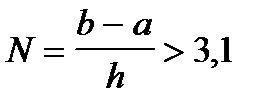, т.е. N=4, h=0,25, .

Составим таблицу значений функции 1/1+x с тремя знаками после запятой, так как .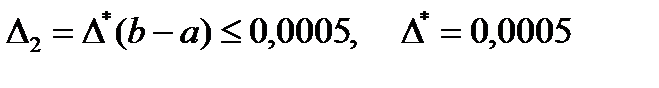

	0,125	0,375	0,625	0,875
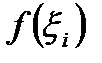
	0,889	0,727	0,615	0,533

Используя формулу, получаем

.

Так как в данном случае погрешность округления равна 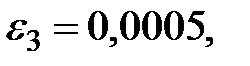, то получим

.

Задание II.

Применяя алгоритм решения задачи 1, находим:

.

Составим таблицу значений функции 1/(1+x) с тремя знаками после запятой

.

	0,00	0,25	0,50	0,75	1,00
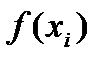
	1,000	0,800	0,667	0,571	0,500

= .

Суммарная погрешность равна

.

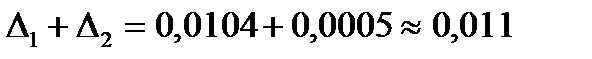и

.

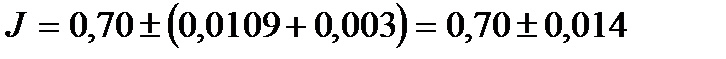Используя формулы (24) и (25) и результаты примера 1, получим

;

;

< ;

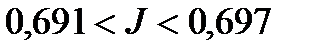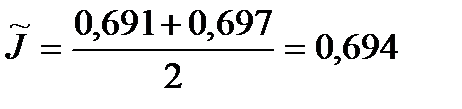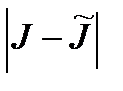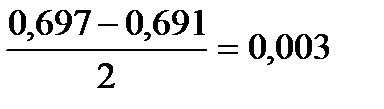Задание III.

Вычислить 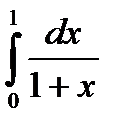по формуле трапеций, полагая N=4; оценить полную погрешность результата. Учитывая результаты примера 1, найти по формуле (24) и оценку (25).

Применяя алгоритм решения задачи II, представим суммарную погрешность 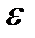в виде суммы трех слагаемых

Выберем 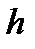из условия

Так как 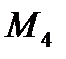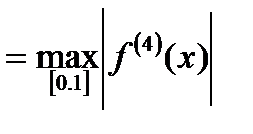= то

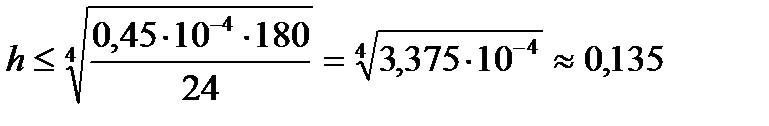и, следовательно,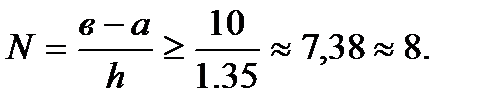

Таким образом, 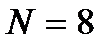, 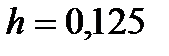и

Составим таблицу значений функций 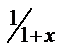с пятью знаками после запятой

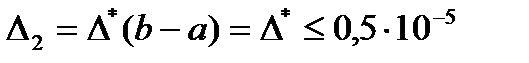
	0,000	0,125	0,250	0,375	0,500	0,625	0,750	0,875	1,000
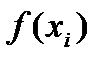
	1,000	0,88889	0,800	0,72727	0,66667	0,61538	0,57143	0,53333	0,500

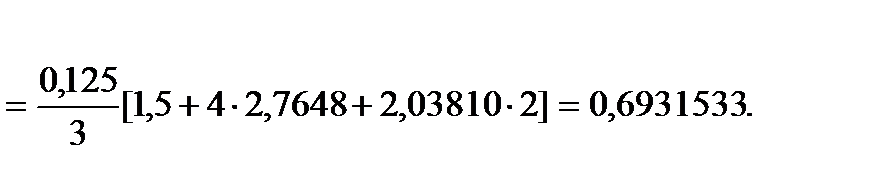
Используя формулу, получаем:

Округляя полученный результат, получим

Глава 8. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Обыкновенные дифференциальные уравнения встречаются очень часто в различных приложениях. При этом в большинстве случаев приходится решать уравнения, общее решение которых не может быть получено в явном виде.

Под получением решения дифференциального уравнения в явном виде обычно понимается получение решения с помощью конечного числа «элементарных» операций: сложения, вычитания, умножения, деления, возведения в степень, логарифмирования, вычисления синуса, косинуса и др.

Еще до появления ЭВМ понятие «элементарной» операции и «элементарной» функции существенно расширилось. Решение некоторых частных задач, в частности дифференциальных уравнений, настолько часто встречались в приложениях, что пришлось составить таблицы их значений, например, таблицы решений дифференциального уравнения Бесселя:

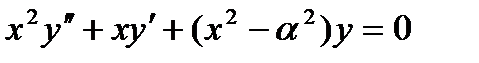, называемых функциями Бесселя, интегрального синуса и т.д.

Эти функции называют специальными функциями. При наличии таких таблиц исчезает принципиальная разница между вычислением функции sinx,lnx… и специальных функций. В том и другом случае можно вычислять значение этих функций при помощи таблиц. Таким образом, в класс дифференциальных уравнений, решение которых может быть получено в явном виде, вошли уравнения, решение которых может быть получено в явном виде. Существенное расширение класса реально решаемых дифференциальных уравнений произошло с созданием приближенных методов решения дифференциального уравнения и реализацией их на ЭВМ.

Некоторые приближенные методы решения дифференциальных уравнений встречаются уже при изучении общей теории обыкновенных дифференциальных уравнений. Так, например, при доказательстве существования решения дифференциального уравнения

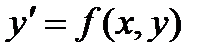(1)

с начальным условием (2)

используют метод последовательных приближений Пикара. В методе Пикара точное решение задачи (1), (2) получается как предел последовательности функций

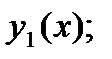
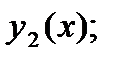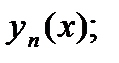… …, (3)

где

… … … … …

(4)

Метод последовательных приближений Пикара сходится, если выполнены следующие условия:

1) функция f(x,y) непрерывна в области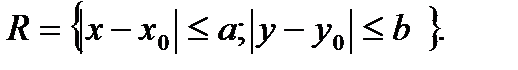

2) функция f(x,y) удовлетворяет R условию Липщица по y:

,

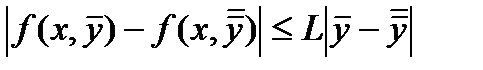где

L – постоянная, не зависящая от 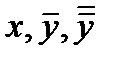, а точки и 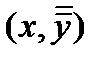- произвольные точки области R.

При выполнении условий 1.,2. последовательность равномерно сходится к функции y(x) на отрезке , где h=min(a,b/M), 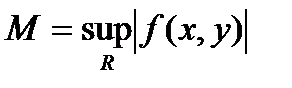и функция y(x) удовлетворяет дифференциальному уравнению (1) и начальному условию (2).

Оценка погрешности приближенного решения 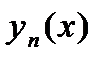на отрезке дается неравенством:

. (5)

Пример 1. Найти три последовательных приближения решения уравнения

(6)

с начальным условием y(0)=0.

Решение. Учитывая начальное условие, заменим уравнение (6) интегральным:

В качестве начального приближения возьмем .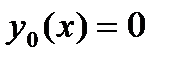

Первое приближение находим по формуле:

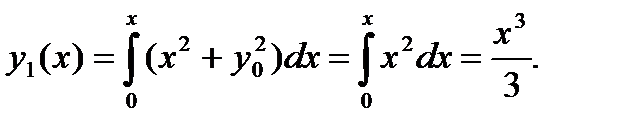
Аналогично получаем второе и третье приближения

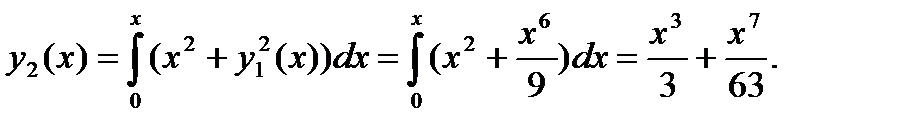
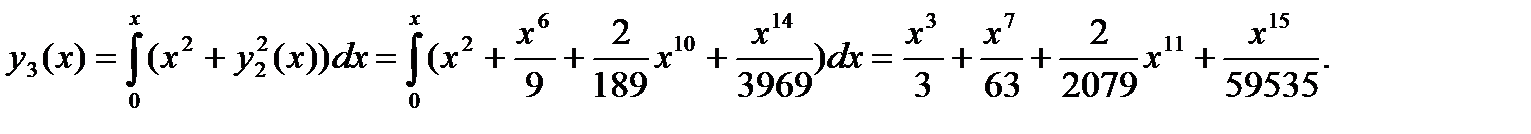
Оценим погрешность третьего приближения по формуле (5). Так как функция 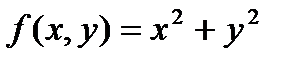определена и непрерывна во всей плоскости, то в качестве а и в можно взять любые числа. Пусть а=1, в=0,5. Тогда

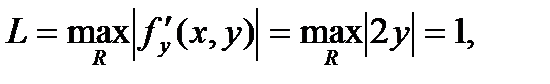
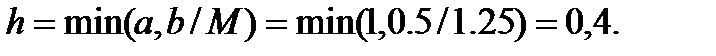
Таким образом, на отрезке получим:

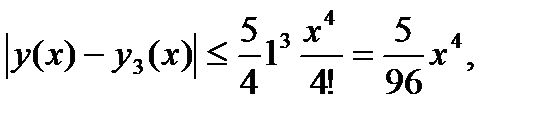
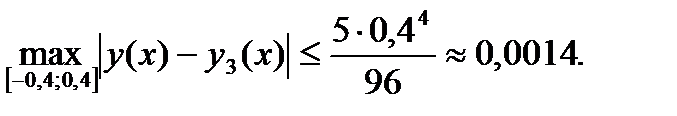
В общей теории обыкновенных дифференциальных уравнений изучается вопрос о возможности представления решения уравнения в виде некоторого ряда.

Пусть требуется найти решение задачи (1), (2).

Предположим, что в рассматриваемой области функция f(x,y) имеет непрерывные частные производные до некоторого порядка n. Тогда искомое решение будет иметь непрерывные производные до порядка n+1, и для решения y(x) справедливо разложение в ряд Тейлора:

(7)

Обозначим . При достаточно малом h мы можем отбросить член и приближенно считать:

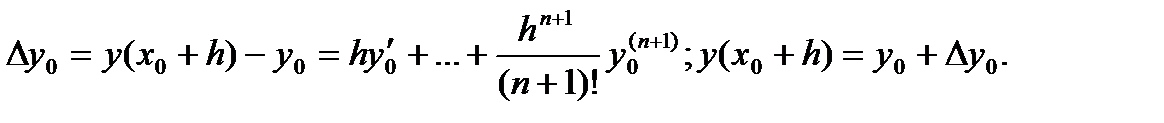(8)

Дифференцируя уравнение по x и подставляя начальное условие, получим выражение для производных, выходящих в (7):

(9)

Пример 2. Найти первые 4 члена разложения в ряд Тейлора решение y=y(x) уравнения (6) с начальным условием y(0)=1.

Решение. Решение уравнения ищем в виде ряда

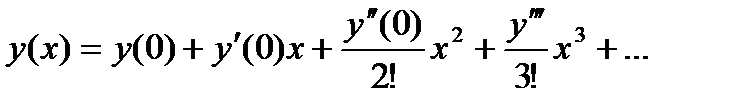
Из начального условия и уравнения (6) имеем

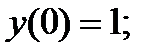
Дифференцируем теперь последовательно по X уравнение (6)

Подставляя начальное условие, находим:

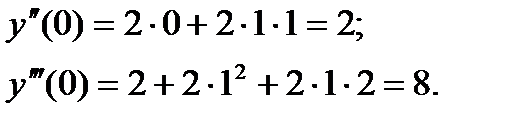
Таким образом, искомое приближенное решение запишется в виде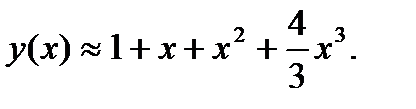

Приближенные методы решения дифференциальных уравнений можно разделить на две большие группы. Одна из них дает приближенное решение в виде аналитического выражения; другая – в виде таблицы. Будем называть первую группу аналитическими методами, вторую – численными. Рассмотренные выше метод последовательных приближений и метод представления решения в виде ряда относятся к аналитическим методам.

Перейдем к изучению численных методов, позволяющих получить таблицу значений решения дифференциального уравнения.

Дата добавления: 2014-12-25