Дотична площина і нормаль до поверхні

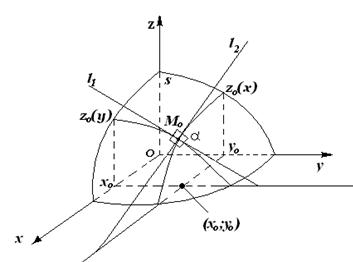Розглянемо одне геометричне застосування частинних похідних функції двох змінних. Нехай функція 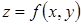диференційовна в точці деякої області. Перетнемо поверхню 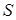, що зображає функцію 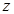, площинами 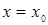і 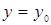(див. рис. 4). Площина 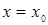перетинає поверхню 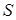по деякій лінії 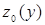, рівняння якої виходить підстановкою у вираз початкової функції 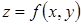замість 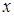числа 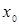. Точка 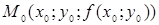належить кривій. Через диференційовність функції 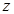в точці 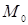функція 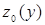також диференціюється в точці 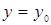. Тому, в цій точці площини 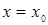до кривої 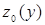може бути проведена дотична пряма .

Рис.4

Проводячи аналогічні міркування для перетину 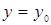, побудуємо дотичну пряму 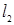до кривої 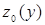в точці 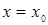. Прямі і 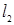визначають площину, яка називається дотичною площиною до поверхні 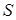в точці .

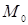Складемо її рівняння. Оскільки площина проходить через точку 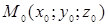, то її рівняння може бути записано у вигляді

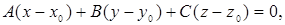
яке можна переписати так:

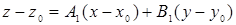(3.1)

(розділивши рівняння на 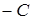і позначивши ).

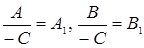Знайдемо 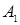і : Рівняння дотичних і 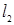мають вигляд

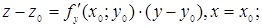
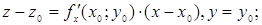
відповідно.

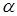Дотична лежить в площині , отже, координати всіх точок задовольняють рівняння (3.1). Цей факт можна записати у вигляді системи

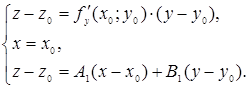
Розв’язуючи цю систему відносно , отримаємо, що 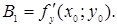Проводячи аналогічні міркування для дотичної 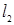, легко встановити, що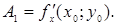

Підставивши значення 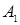і в рівняння (3.1), одержуємо шукане рівняння дотичної площини:

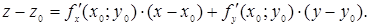(3.2)

Пряма, що проходить через точку 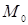і перпендикулярна дотичній площини, побудованої в цій точці поверхні, називається її нормаллю.

Використовуючи умову перпендикулярності прямої і площини (див. з. 87), легко отримати канонічні рівняння нормалі:

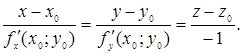(3.3)

Якщо поверхня 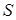задана рівнянням 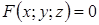, то рівняння (3.2) і (3.3), з урахуванням того, що частинні похідні можуть бути знайдені як похідні неявної функції:

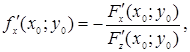
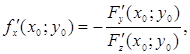
(див. формули (2.12)), приймуть відповідно вигляд

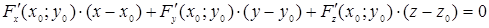і

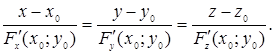
Зауваження. Формули дотичної площини і нормалі до поверхні отримані для звичайних, тобто не особливих, точок поверхні. Точка 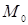поверхні називається особливою, якщо в цій точці всі частинні похідні рівні нулю або хоча б одна з них не існує. Такі точки ми не розглядаємо.

Приклад 1. Написати рівняння дотичної площини і нормалі до параболоїда обертання 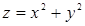в точці .

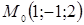m Тут, , ,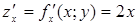

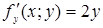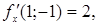
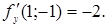
Користуючись формулами (3.2) і (3.3) одержуємо рівняння дотичної площини:

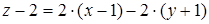або і рівняння нормалі:

l

Дата добавления: 2014-12-26