
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рівняння та нерівності, що містять під знаком абсолютної величини
|
|
|
|
Завдання для самостійної роботи
5.6. Розв’язати нерівності:
а) 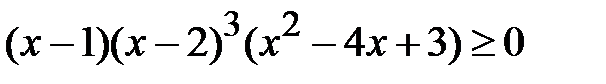 ; b)
; b) 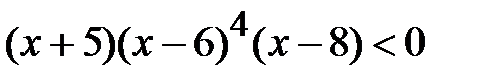 ; c)
; c) 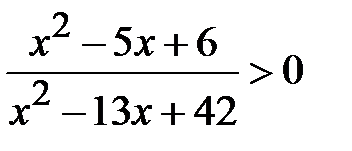 ;
;
d) 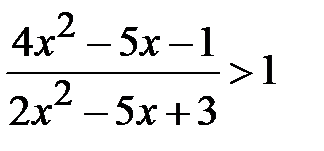 ; e)
; e) 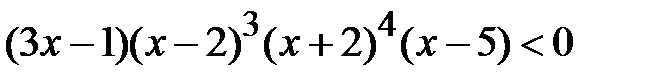 ; f)
; f) 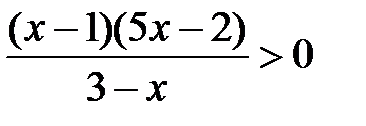 ;
;
g) 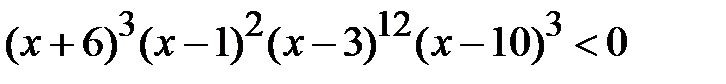 ; h)
; h) 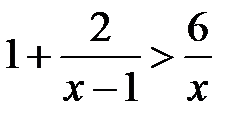 ;
;
i) 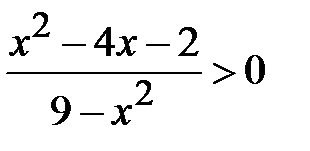 ; j)
; j) 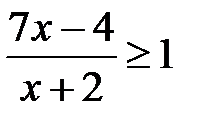 ; k)
; k) 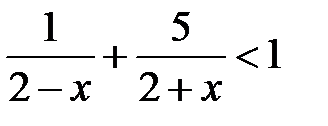 ; l)
; l) 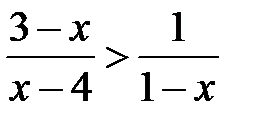 .
.
Нагадаємо означення модуля або абсолютної величини числа: модулем 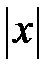 називається само число
називається само число 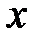 , якщо
, якщо 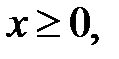 і
і 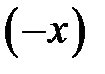 , якщо
, якщо 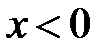 :
:
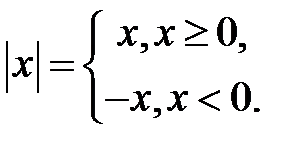
Наприклад, якщо 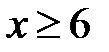 , то
, то 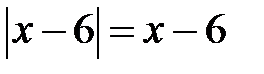 . А у випадку
. А у випадку 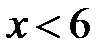 значення модуля таке:
значення модуля таке: 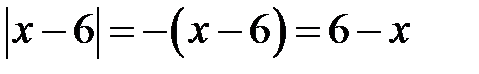 .
.
Геометричний зміст модуля: 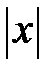 - це відстань від точки
- це відстань від точки 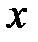 до точки 0 на числовій прямій. Отже, для
до точки 0 на числовій прямій. Отже, для 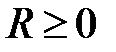 маємо:
маємо:
а) 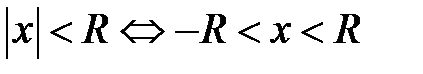 (рис. 5.5); б)
(рис. 5.5); б) 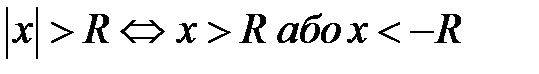 (рис. 5.6);
(рис. 5.6);
в) 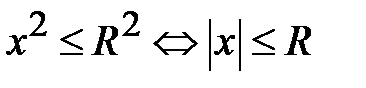 .
.

Рис. 5. 5 Рис. 5. 6 Рис. 5. 7
Корисно запам’ятати також, що 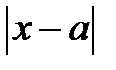 є відстанню на числовій прямій від точки
є відстанню на числовій прямій від точки 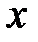 до точки
до точки 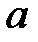 (рис. 5.7).
(рис. 5.7).
Наприклад, на числовій прямій множина точок, що задовольняє умову 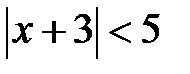 , є інтервал із центром у точці
, є інтервал із центром у точці 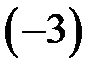 і радіусом
і радіусом 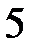 , тобто інтервал від точки
, тобто інтервал від точки 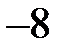 до точки
до точки 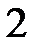 .
.
Приклад 5.12. Розв’язати рівняння 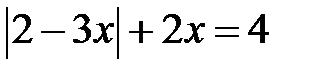 .
.
Розв’язання. Точка 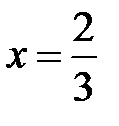 розбиває числову вісь на два проміжки, а саме, якщо
розбиває числову вісь на два проміжки, а саме, якщо 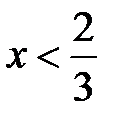 , то вираз під знаком модуля додатний, тому модуль збігається із самим виразом, і маємо систему
, то вираз під знаком модуля додатний, тому модуль збігається із самим виразом, і маємо систему 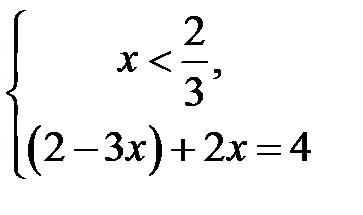 або
або 
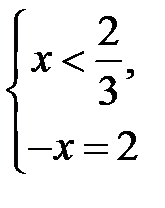 та її розв’язок
та її розв’язок 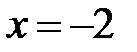 . У протилежному випадку після розкриття знака модуля
. У протилежному випадку після розкриття знака модуля 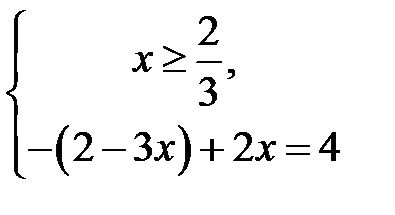 отримаємо
отримаємо 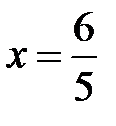 . Відповідь:
. Відповідь: 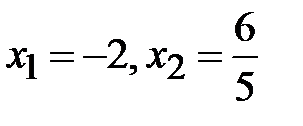 .
.
Приклад 5.13. Розв’язати рівняння 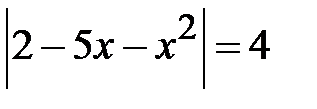 .
.
Розв’язання. Для розв’язання цього рівняння краще безпосередньо проаналізувати означення модуля. Модуль числа дорівнює 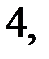 якщо це число
якщо це число  або
або 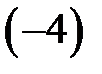 . Наше рівняння можна замінити на два окремих рівняння, які часто записують у вигляді сукупності
. Наше рівняння можна замінити на два окремих рівняння, які часто записують у вигляді сукупності 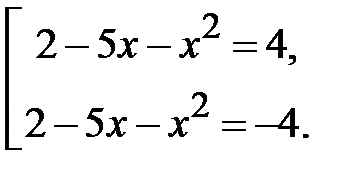 Кожне рівняння розглянемо окремо і отримаємо
Кожне рівняння розглянемо окремо і отримаємо 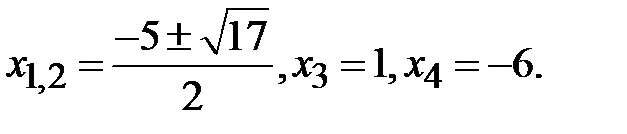
Приклад 5.14. Розв’язати рівняння 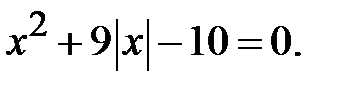
Розв’язання. Перший спосіб - використання заміни змінної, а саме: позначимо 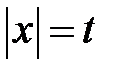 і підкреслимо, що
і підкреслимо, що 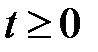 . Розв’язками отриманого квадратного рівняння
. Розв’язками отриманого квадратного рівняння 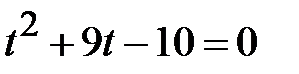 є числа
є числа 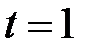 і
і 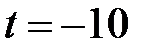 , друге із яких нас не влаштовує. Рівняння
, друге із яких нас не влаштовує. Рівняння 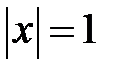 має два корені:
має два корені: 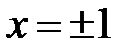 .
.
Рівняння можна було розв’язати інакше, а саме розглянути окремо два випадки: 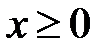 і
і  . Відповідно маємо
. Відповідно маємо 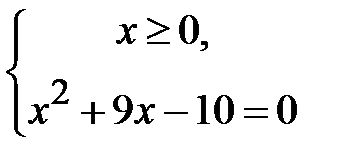 і
і 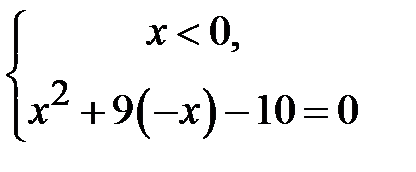 . Першу систему задовольняє число
. Першу систему задовольняє число 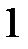 , а другу –
, а другу – 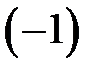 .
.
|
|
|
Приклад 5.15. Розв’язати нерівність 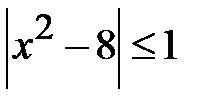 .
.
Розв’язання. Нерівність одразу замінимо на 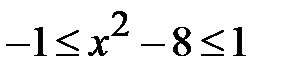 або
або 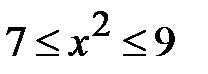 . Відповідь:
. Відповідь: 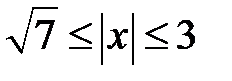 або
або 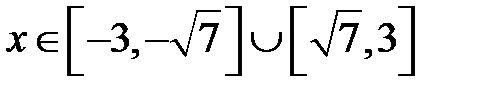 .
.
Приклад 5. 16. Розв’язати нерівність 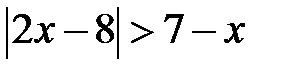 .
.
Розв’язання. Щоб позбавитися знака модуля, розглянемо окремо два випадки: 1) 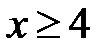 , 2)
, 2) 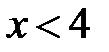 , які приводять до двох окремих систем:
, які приводять до двох окремих систем:
1) 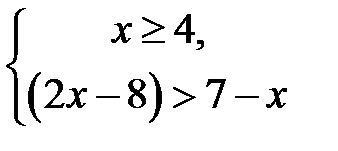 і 2)
і 2) 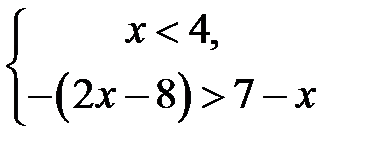 . Перша має розв’язок
. Перша має розв’язок 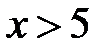 , а друга - розв’язок
, а друга - розв’язок 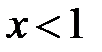 . Тому
. Тому 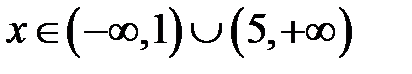 .
.
Зауваження. Розглянуті приклади здаються занадто простими, але у подальшому вони можуть змінювати своє “обличчя” та виникати у досить серйозному вигляді, а тоді має неабияке значення вміння розв’язувати їх швидко та правильно
(див. завдання 5.10)
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 476; Нарушение авторских прав?; Мы поможем в написании вашей работы!