
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 6. Контрольная работа №1. Прием части-1 БДЗ. 3 страница
|
|
|
|
Решение:
Общие формулы: уравнение 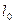 , содержащей точки
, содержащей точки 
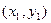 ,
, 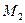
 , записывают в виде:
, записывают в виде: 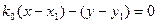 , где
, где 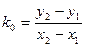 .
.
 Замечание: представлена только основная формула, другие уже использовались в решённых примерах, и будут раскрываться по мере необходимости!
Замечание: представлена только основная формула, другие уже использовались в решённых примерах, и будут раскрываться по мере необходимости!
1). Найдём уравнение прямой 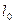 . Вычислим
. Вычислим 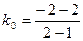 =–4, и запишем уравнение
=–4, и запишем уравнение  :
: 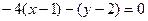 , или в виде
, или в виде  .
.
2). Используя условие 
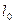 , можем записать
, можем записать 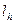 :
: 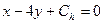 . Вычислим
. Вычислим 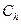 из условия:
из условия:  , то есть:
, то есть: 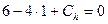 , откуда
, откуда 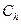 =–2. Окончательно
=–2. Окончательно 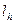 :
: 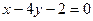 .
.
3). Вычислим 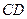 =
= 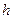 как расстояние от точки
как расстояние от точки  до прямой линии
до прямой линии 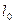 . Нормируем уравнение
. Нормируем уравнение 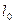 и вычисляем:
и вычисляем: 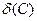 =
= 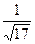 ·
· 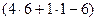 =
= 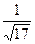 ·19→
·19→ 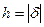 =
= 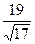 .
.
4). Вычислим угол 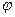 . Если обозначить угловой коэффициент вектора
. Если обозначить угловой коэффициент вектора 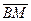 как
как 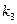 , то, используя величину
, то, используя величину 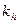 =
= 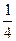 , можем записать:
, можем записать: 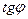 =
= 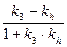 . Вычислим координаты точки
. Вычислим координаты точки  , учитывая, что
, учитывая, что  – медиана:
– медиана:  =
= 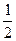
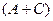 =
= 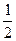 (7,3), тогда
(7,3), тогда 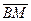 =
= 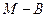 =
= 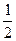 (3,7). Теперь можем записать:
(3,7). Теперь можем записать: 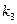 =
= 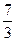 и вычислить
и вычислить 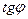 =
= 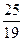 . Используя формулу тригонометрии:
. Используя формулу тригонометрии: 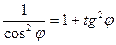 , вычислим
, вычислим 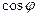 =
= 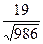 .
.
5). Нахождение уравнений  и
и  можно было бы решать традиционно: имея угловые коэффициенты векторов
можно было бы решать традиционно: имея угловые коэффициенты векторов 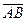 и
и 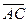 , найти угловые коэффициенты названных прямых и получить нужные уравнения.
, найти угловые коэффициенты названных прямых и получить нужные уравнения.
Мы не станем применять этот способ: он более трудоёмкий. К тому же ответ, используемый задачником, будет получить весьма трудно!
Воспользуемся тем, что биссектриса угла есть геометрическое место точек, равноудалённых от сторон угла!
Найдём уравнение прямой 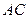 =
= 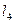 . Вычислим
. Вычислим 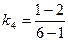 =–
=– 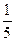 , и запишем
, и запишем 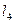 :
: 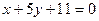 . Легко нормируя уравнения для прямых линий
. Легко нормируя уравнения для прямых линий 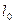 и
и 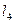 , можем записать:
, можем записать:
 :
: 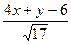 =–
=– 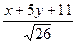 , учтено, что угол
, учтено, что угол 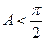 , (5)
, (5)
 :
: 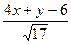 =
= 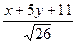 , учтено, что угол
, учтено, что угол 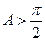 . (6)
. (6)
Замечание: обоснование формул (5) и (6), а также особенности их применения показано в Пособии по аналитической геометрии и в Пособии БДЗ!
Используя записи (5) и (6), достаточно просто получаем записи, используемые в ответах Задачника  :
: 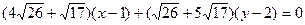 ,
,
 :
: 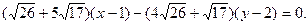
Ответ: уравнения  :
: 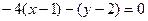 ,
, 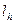 :
: 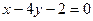 , высота треугольника
, высота треугольника  =
= 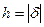 =
= 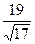 , для угла
, для угла 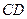 ^
^ 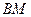 имеем
имеем 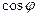 =
= 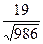 , уравнения биссектрис:
, уравнения биссектрис:  :
: 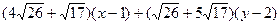 =0,
=0,
|
|
|
 :
: 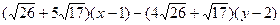 =0.
=0.
Пример 5 – 173: Составить уравнения сторон треугольника, зная одну его вершину  (2, 6), а также уравнения высоты
(2, 6), а также уравнения высоты 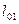 :
: 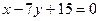 и биссектрисы
и биссектрисы 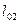 :
:  , проведенных из одной вершины.
, проведенных из одной вершины.
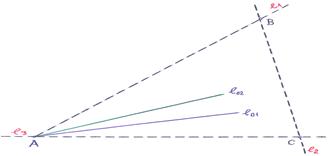 Решение:
Решение:
1). Имея уравнения медианы 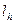 и высоты
и высоты 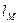 , определим координаты точки
, определим координаты точки  =
= 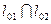 из системы уравнений:
из системы уравнений: 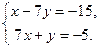 Решение системы:
Решение системы:  = (–1, 2).
= (–1, 2).
2). Уравнение прямой 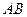 (обозначим
(обозначим  ) определим по свойству принадлежности
) определим по свойству принадлежности 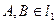 . Так как
. Так как 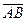 =
= 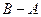 =(3,4), то уравнение прямой
=(3,4), то уравнение прямой  можем записать в виде выражений
можем записать в виде выражений  :
: 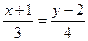 , или
, или 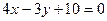 .
.
3). Уравнение стороны 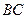 (обозначим
(обозначим  ) определим по свойству
) определим по свойству 
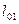 . Сразу можем записать
. Сразу можем записать  :
: 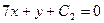 , причём
, причём 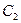 определяется условием:
определяется условием: 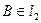 , то есть:
, то есть: 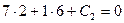 , откуда получаем:
, откуда получаем: 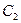 = –20. Окончательно
= –20. Окончательно  :
:  .
.
4). Для прямых  и
и 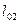 запишем их угловые коэффициенты:
запишем их угловые коэффициенты: 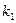 =
= 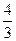 ,
, 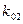 =–7, соответственно. Для прямой линии
=–7, соответственно. Для прямой линии 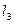 вычислим
вычислим 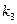 из условия, что
из условия, что 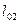 биссектриса угла
биссектриса угла  треугольника:
треугольника:
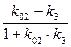 =
= 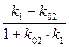 , или
, или 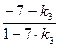 =
= 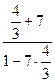 , откуда
, откуда 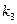 =–
=– 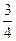 .
.
Так как 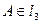 то
то 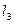 :
: 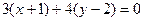 , или
, или 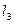 :
: 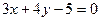 .
.
Ответ: уравнения  :
: 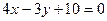 ,
,  :
:  ,
, 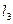 :
: 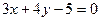 .
.
☻
Вопросы для самопроверки:
1. При помощи какого свойства векторов получают общее уравнение прямой?
2. Как записывается уравнение прямой в параметрической форме?
3. Что значит «уравнение прямой в отрезках»?
4. Как проводится «нормализация общего уравнения прямой»?
5. Что значит «угловой коэффициент» вектора, прямой?
6. Как получают уравнение прямой, проходящей через две заданные точки?
7. Что такое «отклонение» точки от заданной прямой, как его вычисляют?
8. Как определить, лежат ли заданные точки А и В в одной полуплоскости или в разных?
9. Как определить угол между заданными прямыми?
10. Как записывают условия параллельности и перпендикулярности для двух прямых?
11. Как определить внутренний угол заданного треугольника?
Задачи для самоподготовки:
Пример C4 – 1: Прямая линия задана точкой 
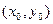 и вектором нормали
и вектором нормали 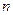 =
= 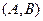 . Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи: в) точка
. Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи: в) точка  (1,1),
(1,1), 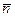 =(2,–1).
=(2,–1).
Ответ: в случае: в) общее 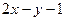 =0, нормальное
=0, нормальное 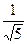 ·(
·(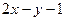 )=0,
)=0,  =
= 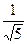 .
.
|
|
|
Пример C4 – 2: Прямая линия задана точкой 
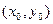 и направляющим вектором
и направляющим вектором  =
= 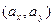 . Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи: в) точка
. Записать уравнение прямой в общем виде, привести к нормальному виду и определить расстояние от начала координат до прямой линии. Рассмотреть случаи: в) точка  (–1,1),
(–1,1),  =(2,0).
=(2,0).
Ответ: в случае: в) уравнения: общее 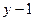 =0, нормальное
=0, нормальное 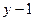 =0,
=0,  =1.
=1.
Пример C4 – 3: Задана прямая линия  и точкой
и точкой 
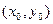 . Вычислить расстояние от точки
. Вычислить расстояние от точки  до
до  . Записать уравнение прямой
. Записать уравнение прямой  , проходящей через точку
, проходящей через точку  перпендикулярно
перпендикулярно  . Записать уравнение прямой
. Записать уравнение прямой  , проходящей через точку
, проходящей через точку  параллельно
параллельно  . Рассмотреть случаи:
. Рассмотреть случаи:
б)  :
: 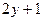 =0, точка
=0, точка  (1,0); в)
(1,0); в)  :
: 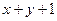 =0, точка
=0, точка  (0,–1).
(0,–1).
Ответ: в случае: б) расстояние:  =
= 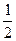 , уравнения
, уравнения  :
: 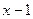 =0,
=0,  :
: 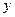 =0, или в каноническом виде
=0, или в каноническом виде  :
: 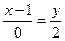 ,
,  :
: 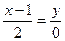 ;
;
в) расстояние:  =0, уравнения
=0, уравнения  :
: 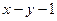 =0,
=0,  :
: 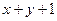 =0, или в каноническом виде
=0, или в каноническом виде  :
: 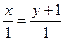 ,
,  :
: 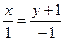 .
.
Пример C4 – 4: Треугольник  задан координатами своих вершин. Записать уравнения прямых линий:
задан координатами своих вершин. Записать уравнения прямых линий: 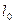 , содержащей сторону треугольника
, содержащей сторону треугольника 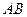 ,
, 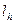 , содержащей высоту
, содержащей высоту 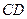 , биссектрис
, биссектрис  внутреннего и
внутреннего и 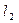 внешнего угла при вершине
внешнего угла при вершине  . Вычислить длину высоты
. Вычислить длину высоты 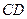 =
= 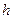 и угол
и угол 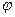 между высотой
между высотой 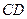 и медианой
и медианой 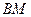 . Рассмотреть случаи: б)
. Рассмотреть случаи: б)  (2,–2),
(2,–2),  (6,1),
(6,1),  (–2,0).
(–2,0).
Ответ: уравнения 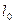 :
: 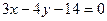 ,
, 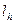 :
: 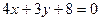 , высота треугольника
, высота треугольника 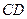 =
= 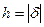 =4, для угла
=4, для угла 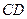 ^
^ 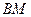 имеем
имеем 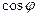 =
= 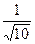 , уравнения биссектрис
, уравнения биссектрис  :
: 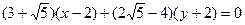 ,
,  :
: 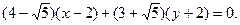 =0.
=0.
< * * * * * >
☺ ☻ ☺
Если в пространстве заданы точка 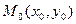 и вектор
и вектор  , перпендикулярный плоскости
, перпендикулярный плоскости  , то уравнение этой плоскости можно записать в виде:
, то уравнение этой плоскости можно записать в виде:
 :
:  = 0, (1)
= 0, (1)
уравнение (1) можно записать в виде: 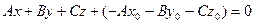 , или
, или 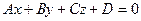 – общее уравнение плоскости.
– общее уравнение плоскости.
Если уравнение 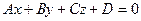 умножить на число:
умножить на число: 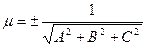 , причём выбирают знак
, причём выбирают знак 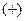 , если
, если 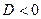 , и знак
, и знак 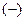 , если
, если 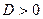 , то получают запись:
, то получают запись: 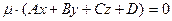 , которую называют уравнением плоскости в нормальном виде. Нормализованное уравнение удобно применять при вычислении отклонения точки
, которую называют уравнением плоскости в нормальном виде. Нормализованное уравнение удобно применять при вычислении отклонения точки 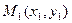 от плоскости
от плоскости  , определяемое выражением:
, определяемое выражением: 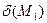 =
= 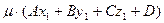 , и расстояния:
, и расстояния: 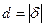 . Нормальное уравнение плоскости также записывают в виде:
. Нормальное уравнение плоскости также записывают в виде:
 :
:  . (2)
. (2)
Если в пространстве заданы три точки 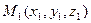 ,
, 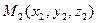 ,
, 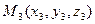 , то уравнение плоскости записывают в виде:
, то уравнение плоскости записывают в виде:
 :
: 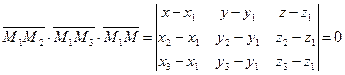 . (3)
. (3)
Выберем точки специально: 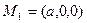 ,
, 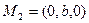 ,
, 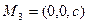 . Получим уравнение плоскости в виде:
. Получим уравнение плоскости в виде: 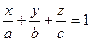 – уравнение в отрезках. (4)
– уравнение в отрезках. (4)
Если прямая линия  в пространстве задана точкой
в пространстве задана точкой 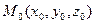 и направляющим вектором
и направляющим вектором 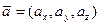 , то её уравнение записывают в виде:
, то её уравнение записывают в виде:
 :
: 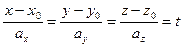 – каноническое уравнение. (5)
– каноническое уравнение. (5)
Частным случаем уравнений (5) являются уравнения для случая, когда заданы две точки: 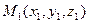 ,
, 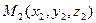 , принадлежащие
, принадлежащие  : достаточно в уравнениях (5) принять:
: достаточно в уравнениях (5) принять:  =
=  и
и 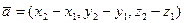 :
:
|
|
|
 :
: 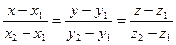 или
или 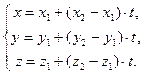 (6)
(6)
Используя уравнения (5), легко получить специальную запись уравнений, широко применяемых в механике:
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 480; Нарушение авторских прав?; Мы поможем в написании вашей работы!