
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 6. Контрольная работа №1. Прием части-1 БДЗ. 4 страница
 :
: 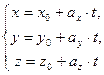 – параметрическая форма уравнений прямой линии. (7)
– параметрическая форма уравнений прямой линии. (7)
При решении многих задач полезно определение прямой в пространстве как линии пересечения двух плоскостей
 :
: 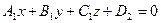 и
и  :
:  .
.
В этом случае уравнение прямой линии  может быть представлено в виде системы уравнений:
может быть представлено в виде системы уравнений:  (8)
(8)
Конечно, система (8) определяет прямую линию лишь в случае, если плоскости пересекаются. Признак пересечения достаточно просто наблюдается: векторы нормалей плоскостей 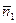 =
= 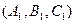 и
и 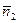 =
= 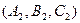 не параллельны!
не параллельны!
Плоскости 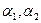 , имеющие общую точку
, имеющие общую точку 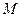 , пересекаются по прямой линии, проходящей через эту точку. Учитывая свойства прямой, можно продолжить: плоскости
, пересекаются по прямой линии, проходящей через эту точку. Учитывая свойства прямой, можно продолжить: плоскости 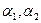 в этом случае имеют бесчисленное множество общих точек. Пусть имеем плоскости:
в этом случае имеют бесчисленное множество общих точек. Пусть имеем плоскости:
Удобно использовать формулы: 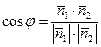 – для вычисления угла между плоскостями
– для вычисления угла между плоскостями  и
и  ;
; 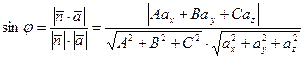 – для вычисления угла между плоскостью
– для вычисления угла между плоскостью  и прямой линией
и прямой линией  .
.
Для нахождения точки пересечения прямой линии с плоскостью применяют общее уравнение плоскости и уравнение прямой линии в виде (7). Тогда:
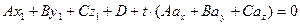 . (9)
. (9)
Вычисляя из (9) значение параметра 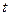 , затем используя уравнения (7), легко получают координаты точки пересечения.
, затем используя уравнения (7), легко получают координаты точки пересечения.
Замечание: представленные формулы 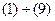 помогут достаточно быстро вспомнить результаты из теории аналитической геометрии, применяемые в рассматриваемом Занятии!
помогут достаточно быстро вспомнить результаты из теории аналитической геометрии, применяемые в рассматриваемом Занятии!
••• ≡ •••
Пример 1 – 182: Составить уравнение плоскости, которая проходит через точку  параллельно векторам
параллельно векторам  и
и 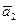 , в случае: а)
, в случае: а)  (1,1,1),
(1,1,1),  =(0,1,2),
=(0,1,2), 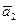 =(–1,0,1); б)
=(–1,0,1); б)  (0,1,2),
(0,1,2),  =(2,0,1),
=(2,0,1), 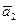 =(1,1,0).
=(1,1,0).
Решение:
Замечание: задачу можно решить не одним способом; для сравнения к случаям а) и б) применим разные способы решения!
Для случая а):
1). Вычисляем вектор нормали плоскости  , используя векторное произведение векторов
, используя векторное произведение векторов  и
и 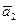 :
: 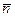 =
= 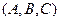 =
= 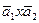 =
= 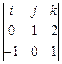 =(1,–2,1).
=(1,–2,1).
2). Запишем общее уравнение плоскости, используя точку  и вектор нормали
и вектор нормали 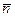 :
:
 :
: 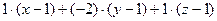 = 0, или
= 0, или  :
: 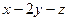 =0.
=0.
Для случая б):
1). Для произвольной точки 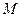 искомой плоскости
искомой плоскости  , построим (используя известное правило) вектор
, построим (используя известное правило) вектор  =
=  =
= 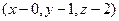 .
.
2). Воспользуемся условием компланарности трёх векторов  ,
,  , и
, и 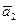 :
: 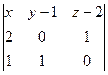 =0, откуда получаем уравнение плоскости
=0, откуда получаем уравнение плоскости  :
: 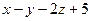 =0.
=0.
Ответ: в случае: а)  :
: 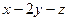 =0; б)
=0; б)  :
: 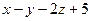 =0.
=0.
Пример 2 – 185: Заданы две плоскости  :
:  =0 и
=0 и  :
:  =0. Определить их взаимное расположение: пересекаются, параллельны или совпадают. Найти расстояние между плоскостями и косинус угла между ними.
=0. Определить их взаимное расположение: пересекаются, параллельны или совпадают. Найти расстояние между плоскостями и косинус угла между ними.
Решение:
1). Для плоскостей  и
и  запишем векторы нормалей:
запишем векторы нормалей: 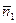 =(–1,2,–1),
=(–1,2,–1), 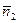 =(0,1,3). Из записи нормалей следует, что плоскости пересекаются. Это значит, что расстояние между плоскостями равно 0.
=(0,1,3). Из записи нормалей следует, что плоскости пересекаются. Это значит, что расстояние между плоскостями равно 0.
2). Вычислим: 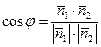 =
= 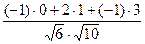 =
=  , где
, где 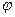 – угол между плоскостями
– угол между плоскостями  и
и  . Учитывая, что угол между плоскостями острый, в ответ запишем значение:
. Учитывая, что угол между плоскостями острый, в ответ запишем значение: 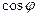 =
= 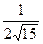 .
.
Ответ: плоскости пересекаются, причём: 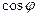 =
= 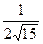 .
.
Пример 3 – 192: Заданы две плоскости. Написать уравнение плоскостей 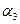 и
и 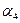 , делящих пополам двугранные углы. Рассмотреть случаи:
, делящих пополам двугранные углы. Рассмотреть случаи:
а)  :
: 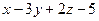 =0 и
=0 и  :
: 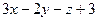 =0;
=0;
б)  :
:  =0 и
=0 и  :
:  =0.
=0.
Решение:
Для случая а):
1). Для плоскостей  и
и  запишем векторы нормалей:
запишем векторы нормалей: 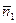 =(1,–3,2),
=(1,–3,2), 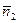 =(3,–2,–1). Нетрудно заметить, что
=(3,–2,–1). Нетрудно заметить, что  =
=  =
= 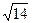 . Из этого следует, что для искомых плоскостей векторы нормалей можно записать в виде:
. Из этого следует, что для искомых плоскостей векторы нормалей можно записать в виде: 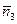 =
= 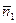 +
+ 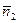 =(4,–5,1) и
=(4,–5,1) и 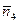 =
= 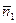 –
– 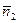 =(–2,–1,3).
=(–2,–1,3).
2). Выделим одну из точек (по усмотрению автора решения!), принадлежащих линии пересечения плоскостей  и
и  :
: 
 . Запишем общее уравнение плоскости:
. Запишем общее уравнение плоскости:
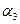 :
: 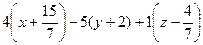 = 0, или
= 0, или 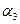 :
:  =0.
=0.
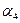 :
: 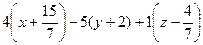 = 0, или
= 0, или 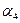 :
: 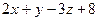 =0.
=0.
Для случая б):
1). Для плоскостей  и
и  запишем векторы нормалей:
запишем векторы нормалей: 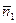 =(2,–1,5),
=(2,–1,5), 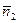 =(1,–5,2). Нетрудно заметить, что
=(1,–5,2). Нетрудно заметить, что  =
=  =
= 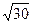 . Из этого следует, что для искомых плоскостей векторы нормалей можно записать в виде:
. Из этого следует, что для искомых плоскостей векторы нормалей можно записать в виде: 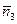 =
= 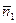 +
+ 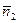 =(3,–6,7) и
=(3,–6,7) и 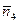 =
= 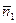 –
– 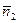 =(1,4,3).
=(1,4,3).
2). Выделим одну из точек (по усмотрению автора решения!), принадлежащих линии пересечения плоскостей  и
и  :
:  (–1,0,1). Запишем общее уравнение плоскости:
(–1,0,1). Запишем общее уравнение плоскости:
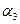 :
: 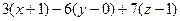 = 0, или
= 0, или 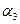 :
: 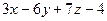 =0.
=0.
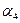 :
: 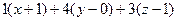 = 0, или
= 0, или 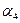 :
: 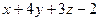 =0.
=0.
Ответ: а) 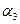 :
:  =0,
=0, 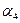 :
: 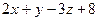 =0; б)
=0; б) 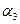 :
: 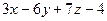 =0,
=0, 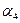 :
: 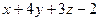 =0.
=0.
Пример 4 – 194: Определить, лежат ли точки  (2,–1,1) и
(2,–1,1) и  (1,2,–3) в одном, в смежных или вертикальных углах, образованных при пересечении двух плоскостей. Рассмотреть случаи: а)
(1,2,–3) в одном, в смежных или вертикальных углах, образованных при пересечении двух плоскостей. Рассмотреть случаи: а)  :
: 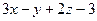 =0 и
=0 и  :
: 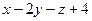 =0.
=0.
Решение:
0). Учитывая, что в рассматриваемой задаче не требуется измерение отклонений при помощи единичного вектора, а достаточно знать только знаки отклонений точек  и
и  от плоскостей
от плоскостей  и
и  , будем использовать непосредственно общие уравнения заданных плоскостей. Подставляя координаты точек
, будем использовать непосредственно общие уравнения заданных плоскостей. Подставляя координаты точек  и
и  в уравнения плоскостей
в уравнения плоскостей  и
и  , получим величины:
, получим величины:  ,
, 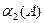 затем
затем  ,
, 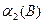 . Сопоставление знаков этих величин позволит определять взаимное расположение точек
. Сопоставление знаков этих величин позволит определять взаимное расположение точек  ,
,  относительно плоскостей
относительно плоскостей  и
и  .
.
 1). Вычислим для варианта а): для точки
1). Вычислим для варианта а): для точки  :
:  =3×2–(–1)+2×3–3>0 и
=3×2–(–1)+2×3–3>0 и  =2–2×(–1)–3+4>0 ® это значит, что точка
=2–2×(–1)–3+4>0 ® это значит, что точка  располагается над плоскостью
располагается над плоскостью  и над плоскостью
и над плоскостью  ; для точки
; для точки  :
:  =3×1–2+2×(–3)–3<0 и
=3×1–2+2×(–3)–3<0 и  =1–2×2–(–3)+4>0. Это значит, что точка
=1–2×2–(–3)+4>0. Это значит, что точка  располагается под плоскостью
располагается под плоскостью  и над плоскостью
и над плоскостью  . Следует: точки
. Следует: точки  ,
,  расположены в смежных углах над плоскостью
расположены в смежных углах над плоскостью  . На рисунке показано положение точек
. На рисунке показано положение точек  ,
,  относительно плоскостей
относительно плоскостей  и
и  , соответствующее полученному решению.
, соответствующее полученному решению.
Замечание: исключение операции нормализации общих уравнений плоскостей  и
и  существенно снижает трудоёмкость решения примера.
существенно снижает трудоёмкость решения примера.
Ответ: в случае а) точки  ,
,  расположены в смежных углах (над плоскостью
расположены в смежных углах (над плоскостью  ).
).
Пример 5 – 196: Составить уравнение плоскости, которая проходит через точку  (1,1,–1) перпендикулярно плоскостям
(1,1,–1) перпендикулярно плоскостям  :
: 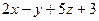 =0 и
=0 и  :
:  =0.
=0.
Решение:
Замечание: задачу можно решить не одним способом; лучше свести к уже использованному решению!
1). Для плоскостей  и
и  запишем векторы нормалей:
запишем векторы нормалей: 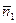 =(2,–1,5),
=(2,–1,5), 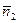 =(1,3,–1).
=(1,3,–1).
2). Примем: 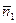 =
=  и
и 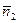 =
= 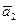 . В таком случае мы имеем Пример 1-182: через точку
. В таком случае мы имеем Пример 1-182: через точку  провести плоскость
провести плоскость  параллельно заданным векторам!
параллельно заданным векторам!
3). Вычислим вектор нормали плоскости  , используя векторное произведение векторов
, используя векторное произведение векторов  и
и 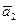 :
: 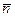 =
= 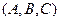 =
= 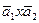 =
= 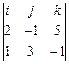 =(2,–1,–1).
=(2,–1,–1).
4). Запишем общее уравнение плоскости, используя точку  и вектор нормали
и вектор нормали 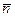 :
:
 :
:  = 0, или
= 0, или  :
:  =0.
=0.
Ответ: уравнение плоскости:  :
:  =0.
=0.
Пример 6 – 198: Составить каноническое уравнение прямой, проходящей через точку 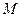 (2,0,–3) параллельно: 1) вектору
(2,0,–3) параллельно: 1) вектору 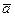 =(2,–2,5); 2) прямой:
=(2,–2,5); 2) прямой: 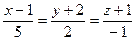 ; 3) оси
; 3) оси 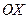 ; 4) оси
; 4) оси 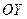 ; 5) оси
; 5) оси 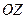 .
.
Решение:
Общее: Каноническое уравнение прямой  :
: 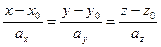 , где
, где 
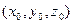 – точка, принадлежащая прямой,
– точка, принадлежащая прямой, 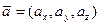 – направляющий вектор прямой. В нашем случае общая точка
– направляющий вектор прямой. В нашем случае общая точка  (2,0,–3) для всех случаев фиксирована. Поэтому
(2,0,–3) для всех случаев фиксирована. Поэтому  :
: 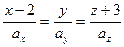 .
.
1). Направляющий вектор задан явно. Имеем  :
: 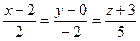 .
.
2). Направляющий вектор задан параллельной прямой. Имеем  :
: 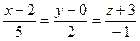 .
.
3). Направляющий вектор неявно задан как единичный вектор оси 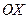 :
: 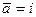 =(1,0,0). Имеем
=(1,0,0). Имеем  :
: 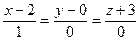 .
.
4). Направляющий вектор неявно задан как единичный вектор оси 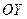 :
: 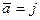 =(0,1,0). Имеем
=(0,1,0). Имеем  :
:  .
.
5). Направляющий вектор неявно задан как единичный вектор оси 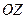 :
: 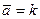 =(0,0,1). Имеем
=(0,0,1). Имеем  :
: 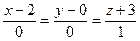 .
.
По всем заданным вариантам получены окончательные результаты: записываем ответ.
Ответ: 1). 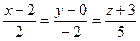 ; 2).
; 2). 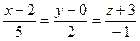 ; 3)
; 3) 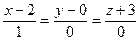 ;
;
4).  ; 5)
; 5) 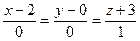 .
.
•◄ Дополнительно ►•
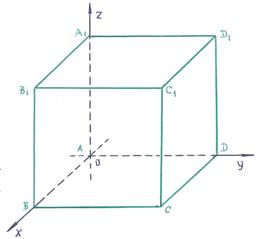
Пример 7 – 218 Куб 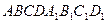 задан своими вершинами:
задан своими вершинами:  =(0,0,0),
=(0,0,0),  =(1,0,0),
=(1,0,0),  =(1,1,0),
=(1,1,0), 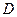 =(0,1,0),
=(0,1,0), 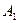 =(0,0,1),
=(0,0,1), 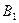 =(1,0,1),
=(1,0,1),  =(1,1,1),
=(1,1,1), 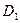 =(0,1,1). Выполнить следующие действия: а) написать уравнения прямых линий
=(0,1,1). Выполнить следующие действия: а) написать уравнения прямых линий 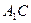 и
и 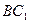 ;
;
б) вычислить расстояние между прямыми линиями 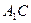 и
и 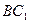 ;
;
 в) написать уравнение общего перпендикуляра между прямыми линиями
в) написать уравнение общего перпендикуляра между прямыми линиями 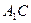 и
и 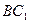 .
.
Решение:
Общее: хотя в геометрии чертёж обычно предназначен только для иллюстрации рассуждений, в рассматриваемом примере с помощью чертежа все задания можем легко выполнить, глядя на чертёж!
|
|
Дата добавления: 2014-12-26; Просмотров: 478; Нарушение авторских прав?; Мы поможем в написании вашей работы!