
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи и упражнения по функциям алгебры логики 1 страница
|
|
|
|
Теорема о полной в Рk системе функций
Cистема функций { max (x 1, x 2), min (x 1, x 2), 0, 1,..., k –1, J 0(x), J 1(x),..., Jk -1(x)} является полной в Рk и любая функция f (x 1,..., xn) Î Pk выражается формулой над этой системой следующим образом:
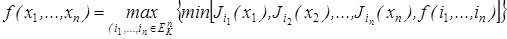 .
.
Эта формула есть своеобразный аналог СДНФ.
Доказательство. Покажем справедливость этой формулы на любом произвольном наборе (a 1,..., an). Слева имеем f (a 1,..., an). Справа имеем 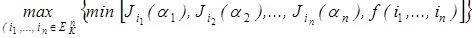 .
.
Если для какого-нибудь j из {1, 2,..., n } ij ¹ aj, то 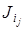 (aj) = 0 и min [ J
(aj) = 0 и min [ J  (a 1),
(a 1), 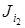 (a 2), …,
(a 2), …, 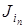 (an), f (i 1,.., in)] = 0. Рассмотрим набор (i 1,..., in), где i 1 = a 1, i 2 = a 2,..., in = an, тогда J
(an), f (i 1,.., in)] = 0. Рассмотрим набор (i 1,..., in), где i 1 = a 1, i 2 = a 2,..., in = an, тогда J 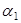 (a 1) = k –1, J
(a 1) = k –1, J 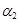 (a 2) = k –1,.., J
(a 2) = k –1,.., J 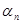 (an) = k –1 и min [ J
(an) = k –1 и min [ J  (a 1),..., J
(a 1),..., J 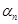 (an) f (a 1, …, an).] = min [(k –1),..., (k –1), f (a 1, …, an).] = f (a 1, …, an), но тогда
(an) f (a 1, …, an).] = min [(k –1),..., (k –1), f (a 1, …, an).] = f (a 1, …, an), но тогда 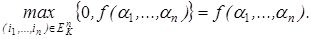 Так как набор (a 1,..., an) произвольный и равенство на нем справедливо, то формула верна. В этой формуле использованы функции Ji (x), (i = 0,..., k –1), min (x 1 x 2), max (x 1 x 2) и константы 0,..., k –1, так как функция f (i 1,..., in) есть число из {0, 1,..., k –1}.
Так как набор (a 1,..., an) произвольный и равенство на нем справедливо, то формула верна. В этой формуле использованы функции Ji (x), (i = 0,..., k –1), min (x 1 x 2), max (x 1 x 2) и константы 0,..., k –1, так как функция f (i 1,..., in) есть число из {0, 1,..., k –1}.
При оперировании с функциями алгебры логики бывают полезны следующие эквивалентности (большинство из них называют обычно основными эквивалентностями алгебры логики). Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей:
1.  – коммутативность связки *, где символ * является общим обозначением для связок &, Ú, Å, ~, |, ¯.
– коммутативность связки *, где символ * является общим обозначением для связок &, Ú, Å, ~, |, ¯.
2.  – ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
– ассоциативность связки *, где *– общее обозначение для связок &,Ú,Å,~.
3. Дистрибутивность
а) 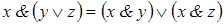 – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
б) 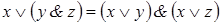 – дистрибутивность дизъюнкции относительно конъюнкции;
– дистрибутивность дизъюнкции относительно конъюнкции;
в) 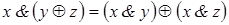 – дистрибутивность конъюнкции относительно сложения по mod 2.
– дистрибутивность конъюнкции относительно сложения по mod 2.
4. а)  ; б)
; б)  суть правила де Моргана;
суть правила де Моргана;
5. а)  ; б)
; б)  суть правила поглощения;
суть правила поглощения;
6. а) 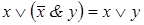 ; б)
; б)  ;
;
7. а) 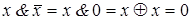 ; б)
; б)  ;
;
в) 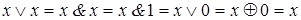 ; г)
; г) 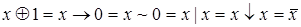 ; д)
; д)  ;
;
8. а)  ;
;
б)  ; в)
; в) 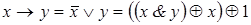 ;
;
9. а) 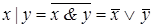 ; б)
; б) 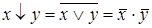 .
.
|
|
|
1. Построить таблицы соответствующих функций, выяснить, эквивалентны ли формулы 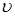 и
и  :
:
1) 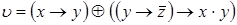 ,
, 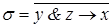 ;
;
2) 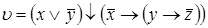 ,
, 
3) 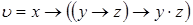 ,
,  ;
;
4)  ,
, 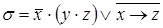 ;
;
5) 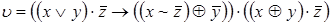 ,
, 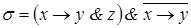 ;
;
6) 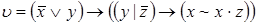 ,
, 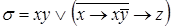 ;
;
7) 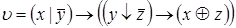 ,
,  ;
;
8) 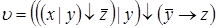 ,
, 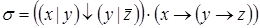 ;
;
9) 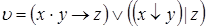 ,
, 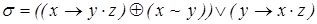 ;
;
10) 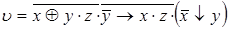 ,
, 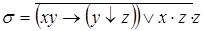 .
.
Ответы: 2), 6), 9), 10) – эквивалентны; 3), 7) – не эквивалентны.
2. Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей:
1) 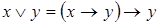 ;
;
2) 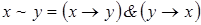 ;
;
3) 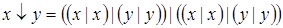 ;
;
4) 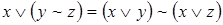 ;
;
5) 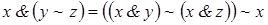 ;
;
6) 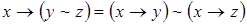 ;
;
7) 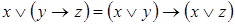 ;
;
8) 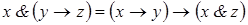 ;
;
9) 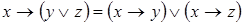 ;
;
10) 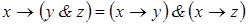 ;
;
11) 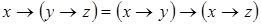 .
.
3. Используя приведенные выше основные эквивалентности и соотношения докажите эквивалентность формул V и U:
1)  ,
, 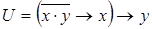 ;
;
2)  ,
,  ;
;
3) 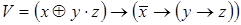 ,
,  ;
;
4) 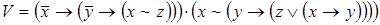 ,
,  ;
;
5) 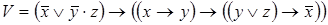 ,
,  ;
;
6) 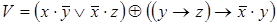 ,
,  ;
;
7) 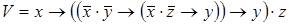 ,
, 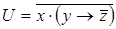 ;
;
8) 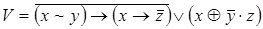 ,
, 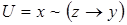 ;
;
9)  ,
, 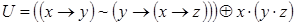 ;
;
10)  ,
,  .
.
Ответы:
4) 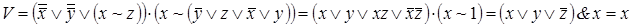
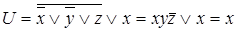 ;
;
9) 

4. Используя непосредственно определение двойственности булевых функций, а также основные эквивалентности и соотношения, выясните, является ли функция g двойственной к функции f:
1) 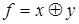 ,
, 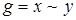 ;
;
2) 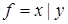 ,
,  ;
;
3)  ,
, 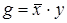 ;
;
4) 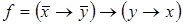 ,
, 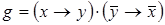 ;
;
5) 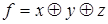 ,
,  ;
;
6) 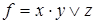 ,
, 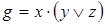 ;
;
7)  ,
, 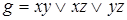 ;
;
8)  ,
, 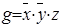 ;
;
9) 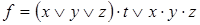 ,
, 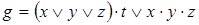 ;
;
10) 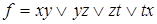 ,
, 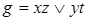 ;
;
11) 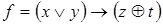 ,
, 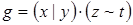 ;
;
12) 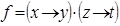 ,
, 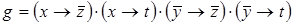 .
.
Ответы: 4)  ,
,  . Значит, g не двойственна к f. 6) – не является; 8),9),11) – является.
. Значит, g не двойственна к f. 6) – не является; 8),9),11) – является.
5. Используя принцип двойственности, постройте формулу, реализующую функцию, двойственную к функции f, и убедитесь в том, что полученная формула эквивалентна формуле V:
1)  ,
,  ;
;
2) 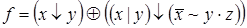 ,
, 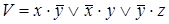 ;
;
3) 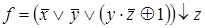 ,
, 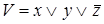 ;
;
4) 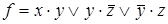 ,
, 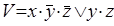 ;
;
5)  ,
,  ;
;
6) 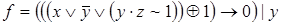 ,
, 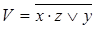 ;
;
7) 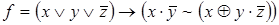 ,
, 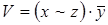 ;
;
8)  ,
, 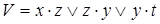 ;
;
9) 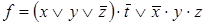 ,
, 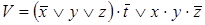 ;
;
10) 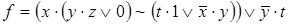 ,
, 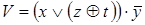 .
.
Ответы:
1) 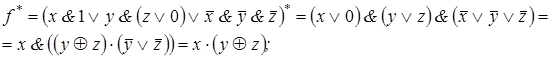
2) 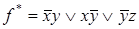 ; 5)
; 5) 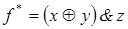 ; 10)
; 10) 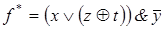 .
.
6. Указать все фиктивные переменные у функции f:
1) 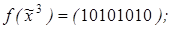
2) 
3) 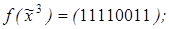
4) 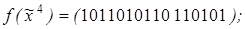
5) 
6) 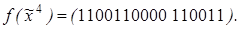
Ответы:1)две фиктивные переменные; 3)одна фиктивная переменная; 5)фиктивные переменные x 1 и x 3.
7. Показать, что x 1 – фиктивная переменная у функции f (реализовав для этой цели функцию f формулой, не содержащей явно переменную x 1):
1) 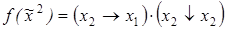 ;
;
2) 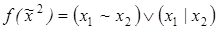 ;
;
3) 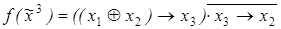 ;
;
4) 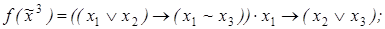 5)
5) 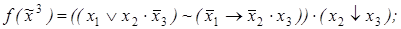 6)
6) 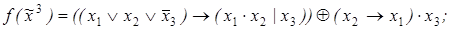 7)
7) 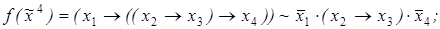
8) 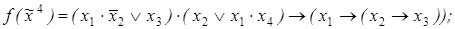 9)
9)  10)
10) 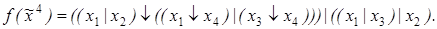
Ответы: 4),8),10) 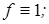 9)
9) 
8. Выяснить, можно ли из функции f, отождествляя и переименовывая в ней переменные, получить функцию g:
1)  ,
, 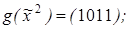
2) 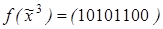 ,
, 
3)  ,
, 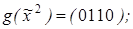
4) 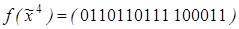 ,
, 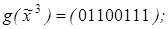
5) 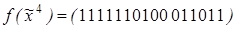 ,
, 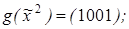
6)  ,
, 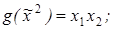
7)  ,
, 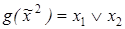 ;
;
8)  ,
, 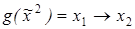 ;
;
9)  ,
, 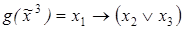 ;
;
10) 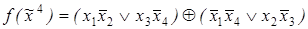 ,
, 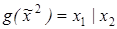 .
.
Ответы: 1),2),5),7),8),9),10)можно. 3),4),6)нельзя.
9. Представить в СДНФ следующие функции:
1) 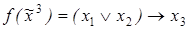 ;
;
2) 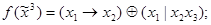
3) 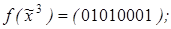
4) 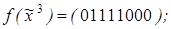
5) 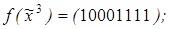
6) 
7) 
8) 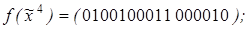
9) 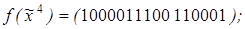
10) 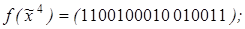
Ответы: 2) 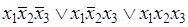 ; 4)
; 4) 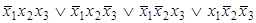 , 7)
, 7) 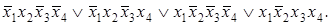
10. Представить в СКНФ следующие функции:
1) 
2) 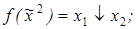
3) 
4) 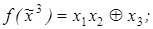
5) 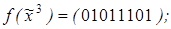
6) 
7) 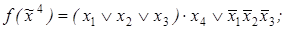
8) 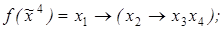
9) 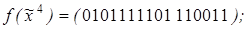
10) 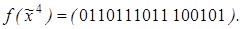
Ответы: 1) 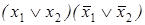 ; 2)
; 2) 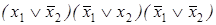 ; 6)
; 6)  ; 8)
; 8) 
11. С помощью эквивалентных преобразований построить ДНФ функции
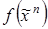 :
:
1) 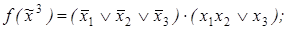
|
|
|
2) 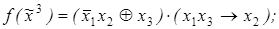
3) 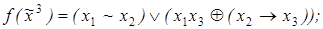
4) 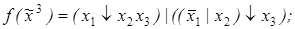
5) 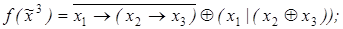
6) 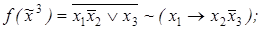
7) 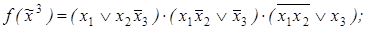
8) 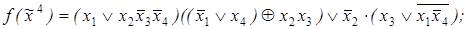
9) 
10) 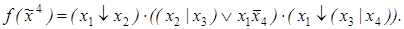
Ответы:
4) 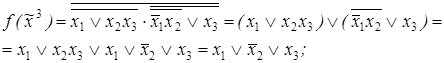
10) 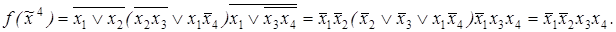
12. Используя эквивалентные преобразования, построить КНФ функции
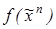 :
:
1) 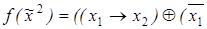
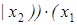


2)  ;
;
3) 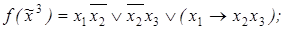


4) 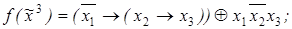
5) 
6) 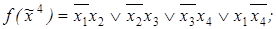
7) 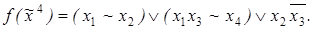
Ответы:
1) 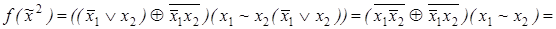

3) 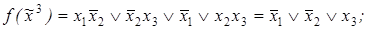
6) 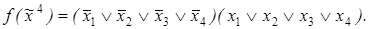
13. Применяя преобразования вида 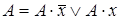 и
и 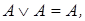 построить из заданной ДНФ функции
построить из заданной ДНФ функции 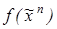 ее совершенную ДНФ:
ее совершенную ДНФ:
1) 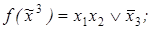
2) 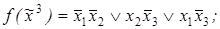
3) 
4) 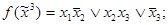
5) 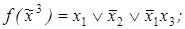
6) 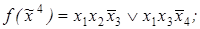
7) 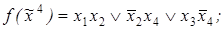
8) 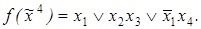
Ответы:
2) 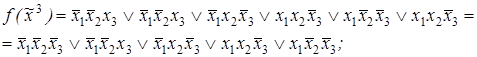
5) 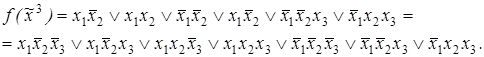
14. С помощью преобразований вида 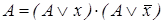 и
и  построить из данной КНФ функции
построить из данной КНФ функции 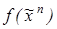 ее совершенную КНФ:
ее совершенную КНФ:
1) 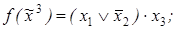
2) 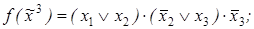
3) 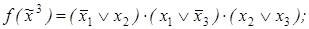
4) 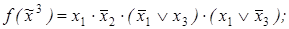
5) 
6) 
7) 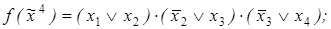
8) 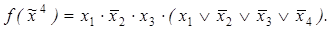
Ответы:
1) 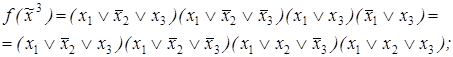
5) 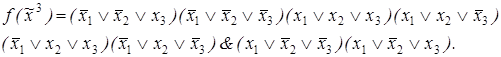
15. Используя дистрибутивный закон 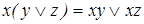 и эквивалентности
и эквивалентности 
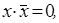

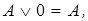 и
и  перейти от заданной КНФ функции
перейти от заданной КНФ функции 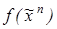 к ДНФ:
к ДНФ:
1) 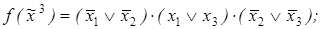
2) 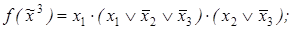
3) 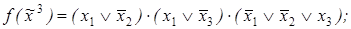
4) 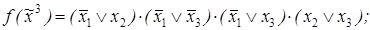
5) 
6) 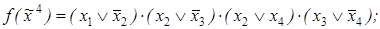
7) 
Ответы:
3) 
6) 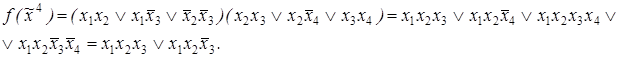
16. Используя дистрибутивный закон 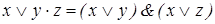 и эквивалентности
и эквивалентности 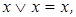
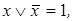
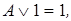
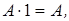 и
и 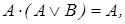 перейти от заданной ДНФ функции
перейти от заданной ДНФ функции 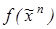 к ее КНФ:
к ее КНФ:
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1659; Нарушение авторских прав?; Мы поможем в написании вашей работы!