Объём пустот, отнесенный к единице объема или массы тела, называют пористостью

Понятие ПЭО предпочтительно определить через понятие пористости, которое является базовым свойством пористой матрицы. Пористость в известном смысле эквивалентно плотности. С целью наглядности, ПЭО можно определить через понятие объёмной плотности скелета (масса скелета в единице объёма пористой среды).

Пусть - математическая точка внутри области занятой пористой средой. Рассмотрим объём (скажем, имеющий форму сферы), с размерами, много больше размеров отдельной поры или зерна, для которого - центроид. Для этого объёма мы можем определить отношение:

,

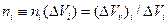где 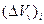- объём пустотного пространства в пределах .

Постепенно сжимая величину , получим последовательность значений объёма вокруг точки в качестве центроида: .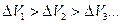

Для больших значений отношение 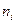может постепенно изменяться по мере того, как будет снижаться, особенно, когда рассматриваемая область – неоднородна (см. рис.1.3). Ниже определённой величины , зависящей от удалённости точки от границы неоднородности, эти изменения или флуктуации будут ослабевать. Останутся только слабые флуктуации, обусловленные случайным распределением размеров пор в окрестности .

Однако, ниже некоторой величины 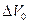, наблюдаются большие флуктуации 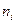. Это возникает вследствие того, что величина достигает характерных размеров отдельных пор. И в завершении, по мере того как 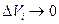, сжимаясь в математическую точку , 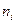становится либо единицей, либо нулём, в зависимости от того в скелете или в пустотном пространстве находится точка .

Что такое объёмная, поверхностная и линейная пористости.

Объёмная пористость пористой среды определяется как предел соотношения 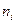по мере того как :

,

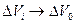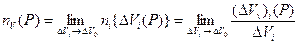где 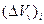- объём пустотного пространства в пределах .

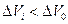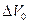Для значений , необходимо рассмотрение реального распределения пор и твердых частиц. В этом диапазоне значение пористости в точке неоднозначно. Объём называется представительным элементарным объёмом (ПЭО) или физической (материальной) точкой пористой среды в математической точке . Из определения ПЭО следует, что его величина такова, что добавление или удаление некоторого количества пор не оказывает существенного влияния на величину 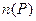. При континуальном подходе полагается, что 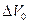и 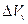достаточно гладки в окрестности .

Тогда:

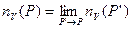
Таким образом, введя понятие пористости и определив ПЭО, мы заменили реальную среду – фиктивным континуумом, в котором мы можем приписать значения определённых свойств некой математической точке.

Аналогично объёмной пористости, можно определить поверхностную и линейную пористости.

Поверхностная пористость пористой среды определяется аналогично объёмной (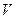 заменяется на S) как предел:

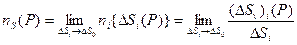
Линейная пористость пористой среды определяется аналогично объёмной и поверхностной (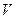 и S заменяется на L) как предел:

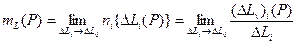
Можно показать, что объёмная, поверхностная и линейная пористости для представительного элементарного объёма совпадают.

При континуальном подходе материя, представляющая собой ансамбль молекул в вакууме заменяется континуумом флюида во всём пространстве. Как результат, мы получаем фиктивную сглаженную среду, называемую флюидом, для каждой точки, которого исследуемые параметры определены как функции координат.

Центральным понятием континуального подхода является понятие «частица». Частица – это ансамбль многих молекул заключенных в малый объём. Размер этого объёма много больше длины свободного пробега молекулы. Однако он должен быть достаточно мал по сравнению с рассматриваемой областью моделирования флюида.

Усредняя свойства флюида и потока по молекулам заключенным в частице и относя полученные значения к центру частицы, получим описание свойств флюида и потока в пределах моделируемой области.

Здесь возникает такое важное понятие как представительность параметра, отражающего свойство флюида. В качестве примера рассмотрим определение плотности флюида.

Плотность есть отношение массы 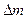вещества к объёму 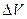, занятому им. Если мы рассматриваем математическую точку и хотим приписать ей величину плотности 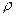, так что это значение должно представлять плотность объёма флюида, для которого эта точка есть срединная точка выбранного центроида, необходимо определить величину объёма.

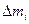Рассмотрим точку во флюиде и, пусть означает массу флюида в достаточно большом объёме , для которого точка является центроидом. Средняя плотность флюида в объёме есть:

Очевидно, если объём слишком велик, скажем, соизмерим с размерами всей моделируемой области, бессмысленно приписывать величину точке , то есть представлять отношение 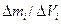для флюида в окрестности точки . Это особенно важно в случае, когда флюид неоднороден. Для того, чтобы определить как мал должен быть объём , для того, чтобы величина плотности была представительна в окрестности точки , мы должны постепенно снижать величину объёма , окружающего точку и, определять для последовательности уменьшающихся объёмов : 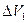> > 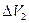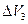…. Результаты подобного подхода представлены на рис. 1.2.

Если мы стартуем с достаточно большого объёма , изменения в величине будут наблюдаться, если флюид неоднороден. Флуктуации вокруг уменьшаются по мере того, как становится меньше.

По мере того, как сжимается к точке , имеет место диапазон значений , на котором величина практически не изменяется с изменением .

Однако, по мере того, как объём становится меньше и количество молекул в нём также становится меньше, дальнейшее снижение ниже определённого значения 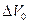где число молекул в настолько мал, что любое дальнейшее снижение заметно влияет на отношение 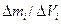. Это происходит, когда характерная длина размера становится порядка величины свободного пробега молекул флюида 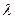. При 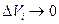наблюдаются большие флуктуации в величине 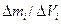. Для этих размеров бессмысленно использовать выше ведённое определение в качестве определения плотности флюида в точке . Таким образом, в качестве определения плотности в некоторой точке можно принять следующее:

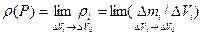
Характерный объём 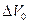называется физической или материальной точкой флюида в математической точке . Объём 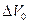может быть идентифицирован с объёмом частицы в точке .

По описанной процедуре, материя, представляющая собой ансамбль молекул в вакууме заменяется континуумом флюида во всём пространстве.

Таким образом, мы получаем фиктивную сглаженную среду, называемую флюидом, вместо ансамбля молекул, для каждой точки, которой функция координат 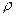определена. Для любых двух близких точек и :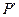

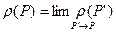
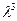
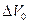
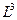
Объём

Рис. 1.2. Определение плотности флюида.

В неоднородном флюиде интересно определить характерную длину :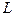

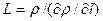
или длину, скажем, в направлении трёх координат:

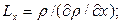
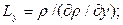
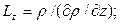
которые характеризуют макроскопические изменения в плотности 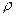в области течения, то есть показывают, насколько быстры эти изменения в величине 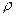. Объём 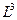(или 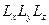) может быть использован в качестве верхнего предела для диапазона изменения , для которого независим от величины . Необходимо отметить, что:

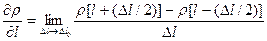
где 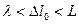, есть характерная длина флюида в точке , с 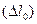порядка .

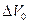Очевидно, когда флюид – газ при очень низком давлении, 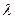, также как и 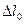, 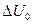могут быть очень большими.

Здесь необходимо ввести безразмерное число 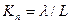, называемое числом Кнудсена. Когда 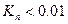, поток флюида может рассматриваться как континуум, для которого применимо макроскопическое рассмотрение, описанное выше (то есть в форме дифференциальных соотношений). Когда 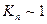мы имеем режим проскальзывания (двухфазный поток со скольжением фаз), и, наконец, если 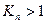мы наблюдаем кнудсеновское течение (свободное молекулярное течение).

При континуальном подходе аналогично вводимому понятию о характерном размере, вводится понятие о характерном времени 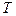. Рассматривая каждую точку на рис. 1.2. как среднее нескольких наблюдаемых за интервал времени 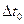, охватывающий рассматриваемый момент времени. Для того, чтобы определить 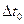, мы должны рассуждать аналогично предыдущему. Интервал времени не должен быть слишком велик, иначе мы потеряем информацию о временном изменении 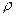, если такие изменения имеют место. То есть интервал времени должен быть меньше чем характерное время 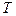, определяемое как 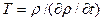. С другой стороны он не должен быть короче, чем среднее время движения молекул между столкновениями. Величина 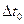может быть получена из кривой подобной изображённой на рис. 1.2., с величиной 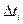в качестве абсциссы и 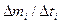в качестве ординаты (см. рис.1.3.).

Многие другие физические явления во флюидах, наблюдаемые через их макроскопические проявления, являются результатом молекулярного движения. Среди них, например, массоперенос посредством молекулярной диффузии, теплопередача, перенос количества движения, проявляющий себя в форме внутреннего трения или вязкости. В каждом из этих случаев, так как мы не можем рассматривать явления переноса на молекулярном уровне, мы усредняем перенос, осуществляемый отдельными молекулами, и переходим на более высокий уровень континуума флюида – микроскопический уровень. Для описания различных транспортных явлений на микроскопическом уровне необходимы соответствующие коэффициенты переноса (молекулярной диффузии, термодиффузии, кинематической вязкости и т.д.). Однако, иногда для понимания явлений или значений микроскопических параметров и их связи с основополагающими молекулярными свойствами, необходимо вернуться обратно к молекулярному уровню.

Итак, мы рассматриваем фильтрующийся флюид как континуум, окружённый твёрдой поверхностью пористой среды. В каждой точке этого континуума мы можем определить удельные физические, динамические и кинематические свойства частицы флюида. Но можем ли мы решить проблему течения в пористой среде на этом уровне. В принципе, мы располагаем результатами теории механики жидкости и газа, так что мы можем рассчитать детали поведения флюидов в пределах пустотного пространства. Например, мы можем, используя уравнение Навье-Стокса для течения вязкой жидкости, удовлетворяющему определённым граничным условиям, скажем занулению скорости на границе флюид – твердая стенка, рассчитать распределение скорости флюида в пустотном пространстве. Однако, это практически невозможно, исключая особенно простые случаи, такие как модель пористой среды, состоящей из прямых капилляров, корректно описать в условиях сложной геометрии твердой поверхности, которая ограничивает область течения в твёрдой пористой матрице. Кроме того, трудно определить сами граничные условия. Чтобы преодолеть эти трудности, необходимо перейти на больший масштаб осреднения – на макроскопический уровень. Это, по-прежнему, континуальный подход, но на более высоком уровне.

В рамках континуального подхода, рассмотрение понятия частица или физическая точка, неразрывно связано с определением представительного объёма. Это особенно важно при движении от микроскопического уровняк макроскопическому уровню. П редставительный объём должен быть значительно меньше размеров моделируемой области, так как подобное усреднение не сможет представить пространственное распределение параметров. С другой стороны п редставительный объём должен быть достаточно велик по сравнению с размерами отдельной поры, которую он включает в себя. Усреднение по большому ансамблю пор, отвечающее требованию континуального подхода, позволяет получать значения, адекватные реальным параметрам пористой среды.

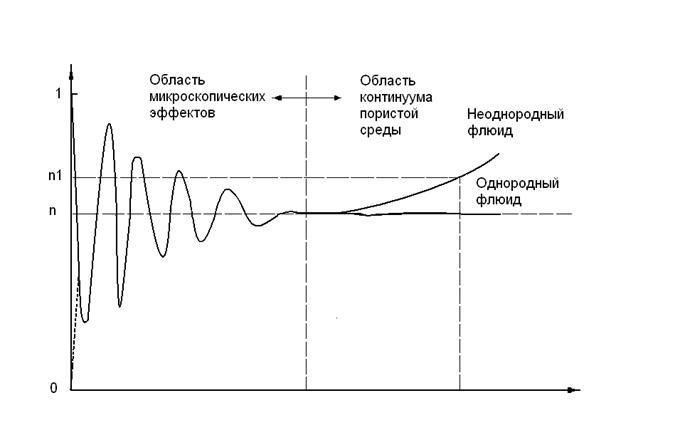
0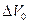

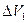
Объём

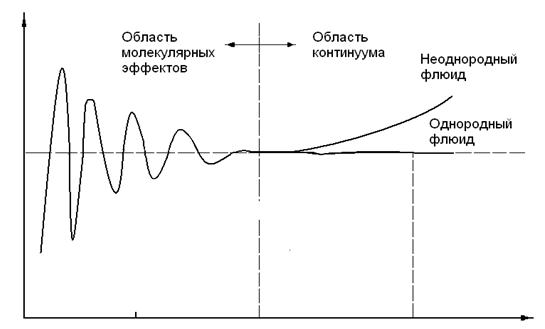
Рис. 1.3. Определение пористости и представительного элементарного объёма.

В случае неоднородных сред (например, с пористостью изменяющейся в пространстве) верхним пределом представительного объёма, должна быть характерная длина, начиная с которой имеют место изменения в величине усредненной по этому объёму пористости. Нижний предел соотносится с размерами пор и зерен (см. рис.1.3.).

Дата добавления: 2014-12-23