Назовите пять числовых характеристик рассеяния случайных переменных, и напишите формулы для вычисления генеральных характеристик и их оценок

Генеральные числовые характеристики рассеяния применяют следующие:

1. генеральный размах ∆ {x} = R {x};

2. генеральное среднее абсолютное отклонение d {x};

3. генеральная дисперсия D {x} = s² {x};

4. генеральное среднее квадратическое отклонение s {x};

5. генеральный коэффициент вариации V {x}*);

Выборочными оценками этих генеральных числовых характеристик являются:

1. выборочная оценка ∆̂ {x} = R̂ {x} размаха;

2. выборочная оценка d̂ {x} среднего абсолютного отклонения;

3. выборочные оценки дисперсии (их две);

4. выборочные оценки среднего квадратического отклонения (их три);

5. выборочная оценка V̂ {x} коэффициента вариации.

Генеральный размах R {x} случайной переменной х ∆ {x} = R {x} = x_max – x_min,

Выборочная оценка размаха вычисляется по формуле:

R̂ {x} = ∆̂ {x} = x̂_max – x̂_min, (2-28)

где x̂_max и x̂_min – выборочные оценки генеральных значений х_max и x_min. Это – приближенная оценка рассеяния. Поэтому основной характеристикой рассеяния считается дисперсия. Размах, применяется при построении интервальных рядов распределения. Он часто применяется на крупном производстве при статистическом контроле качества. использует R̂ {x} для выполнения быстрых статистических

решений

Генеральное среднее абсолютное отклонение d{x}определяется формулами: а) для дискретной случайной величины х:

, (2.29)

где k – номер варианта дискретной случайной величины х, М{x} – её математическое ожидание, p_k – вероятность появления х в k-том варианте, k – общее число дискрет;

б) для непрерывной х:

, (2.30)

где φ(х) – дифференциальная функция распределения.

Выборочную оценку 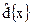среднего абсолютного отклонения для дискретных данных вычисляют по одной из двух формул:

, (2.31)

где j – номер элемента выборки (j = 1; 2; …; N); N – объём выборки; k – номер дискреты (k = 1; 2; …; К); N_к – число элементов в k-той дискрете; 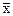- среднее арифметическое

Дисперсия считается основной числовой характеристикой рассеяния случайной переменной и второй основной числовой характеристикой случайной величины (первая - ). В общем случае дисперсию, как оператор, обозначают . Дисперсия генеральной статической совокупности есть математическое ожидание квадрата отклонений значений элементов генеральной совокупности от математического ожидания случайной величины х:

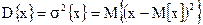. (2.32)

а) для дискретной х генеральная дисперсия определяется суммой:

, (2.33)

Употребляют две оценки дисперсии:

а) Смещенная оценка *):

(2.34)

причём (2.34) применяют для несгруппированных данных, а для сгруппированных по вариантам:

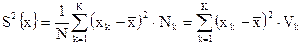, (2.34а)

обозначения здесь прежние. Но оценка является смещенной.

б) Несмещенная оценка дисперсии вычисляется по формуле:

(2.35)

Среднее квадратическое отклонение *) является парамет­ром распределения случайной величине, производит от дисперсии и вычисляется как положительный корень квадратный из дисперсии. Генеральное среднее квадратическое отклонение определяется формулой:

(2.36)

Виды выборочных оценок среднего квадратического отклонения видами оценок дисперсии:

а) Выборочная оценка среднего квадратического отклонения вычисляется по смещенной оценке дисперсии - формула (2.34):

(2.37)

б) Выборочная оценка среднего квадратического отклонения , вычисляемая по несмещенной оценке дисперсии (2.35):

(2.38)

Но так как корень квадратный из некоторой величины есть нелинейная функция то, несмотря на несмещенность оценки 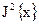, оценка является смещенной. Поэтому применяется еще одна, третья оценка среднего квадратического отклонения.

в) Несмешанная выборочная оценка среднего квадратического отклонения получается, как среднее геометрическое значение из всех возможных оценок . Для облегчения расчётов в справочниках приводится специальная таблица, позволяющая вносить поправки на систематическую ошибку (смещение), в зависимости от числа степеней свободы При этом вычисление несмещенной опенки выполняется по формуле:

(2.39)

Из табл.2.6 видно, что с ростом объема N выборки поправоч­ный коэффициент уменьшается примерно по экспоненте.

Коэффициент вариации – это достаточно широко применяемая числовая характеристика разброса случайной величины, она выражается в относительных единицах (или в процентах). Генеральный коэффициент вариации определяется выражением:

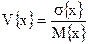
Выборочная оценка коэффициента вариации случайной величии х получается обычно через несмещенную оценку дисперсии, то есть:

(2.40)

Вместо в (2.40) применяется также , вычисляемое по формуле (2.39). Коэффициент вариации, таким образом, выражает ту доли, которую имеет генеральное среднее квадратическое откло­нение (или его оценка) по отношению к математическому ожиданию (или его оценке 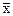). Коэффициент вариации важно учитывать при построении математических моделей сложных объектов.

20. Определите понятия начального и центрального статистических моментов, как они вычисляются?

Статистические моменты являются важными числовыми характе­ристиками распределения случайной переменной, которые позволяют легко осуществлять сравнение свойств различных одномерных слу­чайных величии, даже без построения оценок законов их распреде­ления. Статистические моменты употребляются, в основном, двух видов: а) начальные моменты, когда значения элементов случайной величины отсчитываются относительно начала координат; б) центральные моменты, когда берутся отклонения случайной величины х от центра распределения, в качестве которого принимается математическое ожидание или его оценка .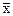

Желающим глубже ознакомиться со статистическими моментами: предлагаем литературу [1-4, 8-12, 15-21].

Здесь рассмотрим центральные статистические моменты различных порядков.

Генеральным центральным статистическим моментом u-того порядка случайной переменной x называется математи­ческое ожидание центрированной случайной переменной 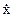, возве­денной в u-тую степень. Центрированной случайной величиной явля­ется разность, характеризующая отклонение каждого j-того элемента случайной переменной x от центра распределения. За который принимается математическое ожидание или его оценка 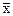, то есть:

Тогда, согласно определение:

(2.41)

Для дискретной х, имевшей k дискрет генеральной совокуп­ности, определяется суммой:

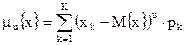(2.42)

Выборочной оценкой центрального статистического метода является величина:

(2.42а)

или

(2.42б)

Можно доказать, что центральный статистический момент первого порядка (u = 1) всегда равен нулю. Действительно, если в формуле (2.42а) положить степень скобки равной I и произвести преобразования, получается:

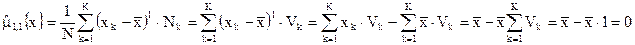
В связи с этим свойством первого центрального момента пользу­ются генеральным абсолютным центральным статистическим моментом первого порядка 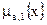, который есть не что иное, как генеральное среднее абсолютное отклонение 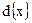(2.29) или для случая выбор­ки его оценка. (2.31).

Генеральный центральный статистический момент второго порядка (u = 2) есть генеральная дисперсия.

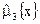Генеральный центральный статистический момент третьего порядка или его оценка характеризуют степень асимметрии кривой дифференциальной функции распределения или ее оценки . Оценку третьего центрального момента можно вычислять по формуле:

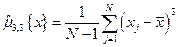
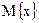Оказывается, что если кривая [или ] симметрична относительно центра распределения (или 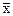), то не только первый центральный момент, но все нечетные моменты (или ) более высоких порядков (u = 3, 5, 7, …) равны нулю.

Для характеристики степени асимметричности распределения на практике пользуются выборочной оценкой коэффициента асимметрии , который является оценкой нормированного центрального момента третьего порядка (u = 3):

(2.43)

и , очевидно, суть величины безразмерные. Для случая правосторонней асимметрии ["хвост" кривой расположен вправо] коэффициент асимметрия > 0 (кривая 1 рис.2.16), а пря левосторонней асимметрии ["хвост" кривой 2 влево] - < 0. Для симметричных кривых = 0 (рис.2.17)

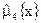Центральный статистический момент четвертого порядка и его выборочная оценка служат числовой харак­теристикой крутости (островершинности или плосковершинности) кривой дифференциальной функции распределения или её оценки . За оценку коэффициента крутости кривой принимают искусственно созданную величину, которую называют оценка коэффициента эксцесса (или просто эксцессом) дифференциальной функции распределения: :

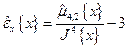(2.44)

На рис. 2.17 изображены кривые , имеющие различные коэффициента эксцесса: I) кривая I нормального закона распределения имеет ; 2) для кривой 2, более крутой, островершинной, чем кривая I ; 3) для кривой 3, более пологой, чем кривая I, . Таким образом, если кривая более островершинная (более крутая), чем кривая нормального закона Гаусса, то коэффициент эксцесса для нее положителен, в противоположном случае - коэффициент эксцесса отрицателен.

Рассмотрение числовых характеристик положения, рассеяния, асимметрии и эксцесса и приведенные примеры вычисления выборочных оценок этих числовых характеристик показывают, что по полученным оценкам можно составить достаточное для практических це­лей представление о характере кривой эмпирического ра­спределения, даже если сама кривая ни задана, по­строена по опытным данным.

21. Какие числовые характеристики применяются для внушения степени асимметрии и крутости кривой ф(х)?

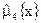Центральный статистический момент четвертого порядка и его выборочная оценка служат числовой харак­теристикой крутости (островершинности или плосковершинности) кривой дифференциальной функции распределения или её оценки . За оценку коэффициента крутости кривой принимают искусственно созданную величину, которую называют оценка коэффициента эксцесса (или просто эксцессом) дифференциальной функции распределения: :

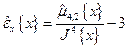(2.44)

Таким образом, если кривая более островершинная (более крутая), чем кривая нормального закона Гаусса, то коэффициент эксцесса для нее положителен, в противоположном случае - коэффициент эксцесса отрицателен.

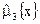Генеральный центральный статистический момент третьего порядка или его оценка характеризуют степень асимметрии кривой дифференциальной функции распределения или ее оценки . Оценку третьего центрального момента можно вычислять по формуле:

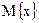Оказывается, что если кривая [или ] симметрична относительно центра распределения (или 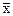), то не только первый центральный момент, но все нечетные моменты (или ) более высоких порядков (u = 3, 5, 7, …) равны нулю.

Для характеристики степени асимметричности распределения на практике пользуются выборочной оценкой коэффициента асимметрии , который является оценкой нормированного центрального момента третьего порядка (u = 3):

(2.43)

и , очевидно, суть величины безразмерные. Для случая правосторонней асимметрии ["хвост" кривой расположен вправо] коэффициент асимметрия > 0 (кривая 1 рис.2.16), а пря левосторонней асимметрии ["хвост" кривой 2 влево] - < 0. Для симметричных кривых = 0 (рис.2.17)

22.Дайте определение корреляционного момента, корреляционного коэффициента, как они вычисляются?

чтобы эффективно управлять технологическим процессом, на­до знать, как сильно и в каком направления тот или иной входной фактор воздействует на определенную выходную характеристику ка­чества продукции. Числовая характеристика, определяющая тесноту связи между случайными переменными и v, называется моментом парной корреляции и определяется по формуле (для выборки)

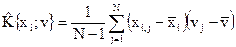(2.45)

Но на практике чаще применяется нормированный момент корреляции, называемый коэффициентом парной корреляция (оценка):

(2.46)

где - средняя величина i-го фактора в N наблюдениях (j = 1; 2; …; N; i = 1; 2; …; n);

n – число факторов;

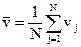- средняя величина характеристики качества в тех же N наблюдениях;

- средние квадратическое отклонения, соответственно, фактора и целевой функции v.

Геометрическая интерпретация корреляционного момента пред­ставлена на рис. 2.18. Такое изображение двумерной статистической совокупности, когда каждое одновременное наблюдение за двумя случайными переменным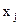и и в статистическом объекте, в котором действуют случайные помехи ε (рис.2.19), отмечается одной точ­кой в системе координат (x; v), с абсциссой 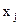и соответ­ствующей ординатой , называют полем корреляции*). На рис.2.18 занесем вертикальную пунктирную линию, соответствующую среднему арифметическому значению 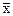и горизонтальную - на уровне .Обозначим отклонения от 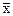и :

(2.47)

Перенесем начало координат в точку , являющуюся точкой пересечения пунктирных лини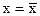й и и обозначим геометрические квадранты I, II, II, IV относительно нового начала координат . В каждом квадранте проставим знаки: если j-я точка попала в I или III квадранты, то знаки у и будут одинаковыми, но если точка попала в квадранты II и IV, то знаки и окажутся разными. А от сочетания знаков и зависит и знак их

произведения в (2.45). На примере, приведенном на рис. 2.18, большинство точек находятся в квадрантах I и III, т.е.оценке будет иметь положительный знак. Вели бы большинство точек попарно в квадранты II и IV, то оценка (2.46) имела бы отрицательный знак. Очевидно, что при симметричном расположении точек поля корреляция относительно горизонтальной линии или относительно вертикальной 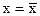оценка корреляционного момента равна нулю (идя близка к кулю), так как каждому положительному; произведению будет соответствовать такое же по абсолютной величине произведение, по с отрицательным знаком.

23. Что такое эмпирическая и теоретическая линия регрессии?

Переменная величина v называется функцией от переменной х, называемой аргументом, если при заданном значении аргумента х зависимая переменная v принимает одно единственное значение, - такая связь называется функциональной (рис. 2.21). Кроме функциональной связи существует также вероятностная. Вероятностная связь имеет два частных случая - корреляционную и дисперсионную связь. Если при изменении одной величины линейно изменяются только средние значения другой (и наоборот), а дисперсия и тип закона распределения остаются неизменными, такая связь называется корреляционной (рис. 2.18). Если не меняется только дисперсия, а среднее арифметическое постоянно, то это дисперсионная связь (рис.2.20). Уравнение, описывающее эти связи называется уравнением регрессии.

Для пояснения и раскрытия физической сущности уравнения регрессии рассмотрим некоторое поле корреляции (рис. 2.22) Разобьем весь размах точек по оси х на k разных интервалов (как это мы делали при построении интервальных рядов распределения в раздела 2.2). Подсчитаем число точек в каждом k-том интервале и отдельно для каждого k-того интервала вычислим средний отклик по точкам, попавшим в этот интервал. Отнесем середине k-того интервала по оси х, и отметим его значе­ние на графике точкой с кружком, затем все k полученных точек соединим отрезки прямых. Получаем ломаную линию, называемую экспериментальной линией регрессия. Если увеличивать общее число N опы­тов и одновременно, но не столь же быстро уменьшать ширину интер­валов . (чтобы число точек в каждом интервале не уменьша­лось, а, неограниченно возрастало), то ломаная линия будет становиться все более плавной, а при она превратится з теоретическую линию регрессии.

На рис. 2.18_, 2.22, приведенных пояснений следует вывод, что по линии регрессии невозможно предсказать точное значение отклика в одиночном опыте при фиксированном значении фактора 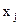, но она позволяет судить, какое в среднем будет значение отклика , если при фиксированном 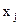независимо выполнить достаточное число 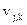опытов. Таким образом» с помощью уравнения регрессии можно выявлять основную закономерность и управлять технологическими процессами (ТП), которые подвержены случайным помехам ε. Математическую модель объекта в общем виде можно записать(рис.2 19):

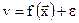, (2.48)

где - вектор факторов;

ε - случайные помехи.

С целью решения практических задач, в частности, для выделения и уточнения состава наиболее существенных факторов, влияющих на характеристики качества, а также для составления математических описаний различных технологических процессов, используют математическую модель в виде ряда Тейлора.

(2.49)

где - вектор неизвестных оценок коэффициентов;

- вектор входных переменных (факторов);

v - выходной показатель (отклик);

ε - неизвестная случайная ошибка.

Причем на предварительных этапах исследований ТП стремятся к простейшей модели, включающей только линейные члены (первого порядка), а на последующих этапах постепенно усложняют вид математической модели. Число членов разложения Тейлора (2.49) определяется свойствами объекта и требованиями заданной точности математической модели: она должна адекватно, то есть достаточно хорошо (с ошибкой не более заданной) аппроксимировать опытные точки и предсказывать функцию отклика в нужной точке факторного пространства. Способы нахождения оценок коэффициентов в разложения Тейлора (2.49) рассмотрены в [29].

Уравнение регрессии позволяет судить:

а) какие факторы реально воздействуют на процесс;

б) какие из выходных переменных следует считать наиболее существенными и какие - несущественными;

в) как сильно и в каком направлении изменяется выходной показатель качества под воздействием каждой из контролируемых входных переменных;

г) как взаимодействуют между собой входные переменные, т.е. как одновременное изменение двух или нескольких входных переменных изменяет выходные показатели процесса:

д) какое значение отклика можно ожидать в интересующей исследователя точке факторного пространства, т.е. при фиксированных значениях факторов;

е) аттестование технологических процессов и т.д.

Дата добавления: 2015-04-24