Назовите четыре числовых характеристики положения случайных переменных и напишите формулы для вычисления генеральных характеристик и их оценок

Напишите аналитическое выражение для нормального закона распределения Гаусса.

Наиболее распространённым и типичным для массовых случайных явлений природы является нормальный закон Гаусса. Известны также законы распределения Пуассона, биномиальный и другие.

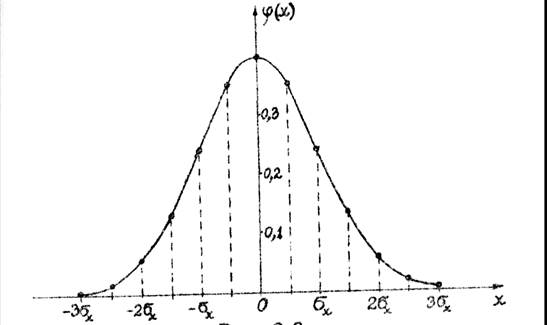
Аналитическое выражение кривой j (х) нормального закона Гаусса имеет вид:

j (х) = (1/(Ö2p×s{x}))×e^{- (x – M{x})²/(2s²{x})}, (2-19)

где М {х} – математическое ожидание, а s²{x} – генеральная дисперсия. Кривая (2-19) имеет колоколообразный вид, она симметрична относительно М {x} Нормальный закон распределения занимает среди других законов распределения особое положение. Это объясняется тем, что, во-первых, он наиболее часто встречается на практике, и, во-вторых, он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. что сумма достаточно большого числа (n ® ¥) независимых случайных величин, подчинённым каким угодно законам распределения приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем больше количество случайных величин.

1. математическое ожидание M {x};

Математическое ожидание М{x} случайной величины х (называемое также генеральным средним арифметическим) определяется формулами:

а) для дискретной случайной переменной:

_K

M {x} = S x_k×p_k, (2-20)

^k=1

где k – номер варианта (дискреты); К – общее количество возможных вариантов x_k (k = 1; 2; …; K); p_k – вероятность появления х в варианте x_k (вероятность p_k играет роль ²веса² каждого x_k);

б) для непрерывной случайной величины:

_¥

М {x} = ò x×j (x)×dx, (2-21)

^-¥

где j (х) – дифференциальная функция распределения.

Важно знать геометрическую интерпретацию математического ожидания непрерывной случайной величины: М {x} есть абсцисса центра тяжести площади под кривой j (х). Из рис.

Выборочное среднее арифметическое `х рассчитывается как отношение суммы всех N значений элементов х _j выборки к числу N элементов. Если дискретная случайная величина х имеет K неповторяющихся вариантов х_k (k = 1; 2; …; K) и известно число N_k элементов в каждом варианте х_k выборки, то таких сгруппированных данных рекомендуется формула, позволяющая убыстрить вычисления:

_{K K}

х = 1/N S x_k×N_k = S x_k×n_k (2-22)

^{k=1 k=1}

2. Генеральная медиана (или просто медиана) Ме {x} – это такое значение случайной величины х, которое обладает свойством равной вероятности того, окажется ли х больше или меньше Ме {x}. Для дискретной х медиана есть такое значение случайной величины x = =Me {x}, которое удовлетворяет условию: число N_-Me – элементов совокупности со значениями x < Me {x} равно числу N_+Me элементов со значениями x > Me {x}. Для непрерывной х медиана делит пополам площадь под кривой j (х). Иллюстрация дана на рисунке 2.11, где заштрихованная часть площадь под кривой j (х) должна быть равна незаштрихованной.

Выборочная оценка медианы х =`Ме {x} определяется в ряду элементов выборки, расположенных по возрастанию их величины. Если число элементов выборки не чётное, например, N = 2M + 1, то оценкой медианы служит (M + 1)-й элемент x_M+1 в этом ряду. Если число элементов выборки чётное, например, N = 2M, то оценка медианы лежит посредине между x_M и x_M+1 и определяется как среднее арифметическое из этих двух элементов.

3.генеральная мода Mo {x};

Генеральная мода Мо {х} – для дискретной случайной величины х – это наиболее вероятное её значение, а для непрерывной – это такое её значение, при котором плотность вероятности случайной величины х максимальна – в этой точке j (х) имеет максимум (рис. 2.11). На практике встречаются случаи полимодального (рис. 2.12) и антимодального (рис. 2.13) распределения.

Выборочная оценка моды х̑ = `Мо {x} для дискретной случайной величины – тот k-тый вариант х̑ = x_k, для которого относительная частота n_k максимальна. Но строго говоря, такой способ нахождения оценки х̑ моды справедлив лишь для такой случайной переменной, у которой дискреты х_k равномерно размещены на числовой оси. При неравномерном распределении дискрет следует оценивать моду интервальным способом по формуле:

х̑ = х_Мо + dх ×((N_k – N_k-1)/(N_k – N_k-1)+(N_k – N_k+1)), (2-24)

где х_Мо – абсцисса начала модального интервала; dх – ширина интервала ряда распределения (dх_k = const); N_k – число элементов в модальном интервале; N_k-1 – то же в домодальном и N_k+1 – то же в послемодальном интервалах.

4.Генеральная середина размаха (центр) Mc {x}.

Генеральная середина размаха (центр) М_с {х} может быть получена лишь для случайных величин, расположенных на ограниченном слева и справа интервале (x_min; x_max):

М_с {x} = x_min + ((x_max – x_min)/2) = ½ (x_max + x_min) (2-25)

Выборочная оценка х̈́ =`М_с {х} может быть получена для любой конечной выборки (N» ¥):

х̈́ = ½ (х̂_min + x̂_max). (2-26)

Различие между (2-25) и (2-26) состоит в том, что В (2-25) х_min и x_max являются генеральными крайними значениями совокупности, а в (2-26) х̂_min и x̂_max – выборочными значениями, причём, в общем случае х̂_min > х_min, а x̂_max < x_max. Примером ограниченного распределения может служить равномерное распределение (рис. 2.14).

Дата добавления: 2015-04-24