Теорема 16.1.(Больцано, Коши) Пусть функция непрерывна на отрезке и принимает на его концах значения разных знаков. Тогда существует хотя бы одна точка такая, что

Вопрос 16: ПРОМЕЖУТОЧНЫЕ ЗНАЧЕНИЯ НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ ФУНКЦИИ

Определение 16.1. Пусть функция определена на некотором множестве . Если она непрерывна в каждой точке этого множества, то говорят, что она непрерывна на множестве .Иными словами, функция непрерывна на множестве , если для любого числа и любого существует такое число 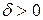, что для всех 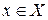, удовлетворяющих неравенству выполняется неравенство .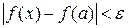

$Пусть, для определённости, 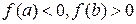. Обозначим 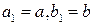и рассмотрим точку 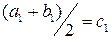. Если оказалось, что 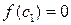, то теорема верна при . Если же , то либо 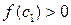и в этом случае положим 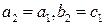, либо 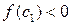и в этом случае положим 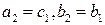. В обоих случаях получен отрезок 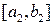, длина которого равна половине длины отрезка 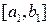и на концах которого функция принимает значения разных знаков.

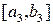Разделим этот отрезок пополам точкой . Если , то теорема верна при . Если же , то либо и в этом случае положим , либо и в этом случае положим . Снова обоих случаях получен отрезок , длина которого равна половине длины отрезка и на концах которого функция принимает значения разных знаков.

Продолжим процесс деления отрезков пополам. При этом возникают две возможности. Либо на каком- то шаге получаем, для , и 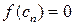. Тогда теорема справедлива. Либо для всех выполняются неравенства 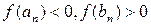. Тогда получается бесконечная система стягивающихся отрезков. Действительно, по построению каждый следующий отрезок вложен в предыдущий, а длина отрезка , равная , стремится к нулю при . Эти отрезки имеют общую точку, которую будем обозначать . Докажем, что .

Действительно, с одной стороны, , поэтому, по теореме о предельном переходе в неравенствах, , так как функция по условию непрерывна на отрезке и 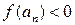. С другой стороны, 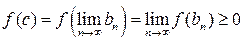, так как 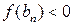. Полученные неравенства доказывают, что . #

Дата добавления: 2015-04-24