Замечание 1 к следствию 1. Это следствие ещё называют основной леммой теории неопределённого интеграла

Следствия теоремы Лагранжа

Следствие 1. (критерий постоянства функции на интервале ). Функция f(x), дифференцируемая на (a, b) (где (a, b) может быть и бесконечным интервалом) является постоянной тогда и только тогда, когда f′(х) = 0 для всех x 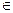(a, b).

◄То, что производная постоянной функции равна 0 уже доказано. Докажем теперь, что если производная функции, определённой на интервале, равна 0, то эта функция является постоянной.

Для этого возьмём две произвольные точки x₁, x₂ 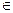(a, b), для определённости пусть x₁‹x_2. Так как всюду на (a, b) существует производная, функция f(x) непрерывна на (a, b), следовательно, и на [x₁, x₂] (a, b). По теореме Лагранжа f(x₂) – f(x₁) = f′(ξ)(x₂ – x₁) = 0, так как f′(ξ) = 0 по условию. Это означает, что значения функции y = f(x) в любых двух точках x₁, x₂ 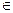(a, b) одинаковые. Но это означает, что f(x) – постоянная. ►

Замечание 2 к следствию 1. Если f′(х) = 0 для всех x 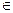X, где X – объединение нескольких интервалов, то f(x) принимает постоянное значение на каждом из интервалов, своё для каждого интервала.

Теорема 24.2 (Коши) Пусть f(x),g(x) 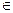C[a, b], f(x), g(x) 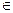D(a, b), 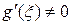для всех точек . Тогда существует точка с 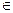(а, b) такая, что

.

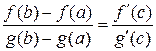◄Доказательство во многом подобно доказательству теоремы Лагранжа. Рассмотрим вспомогательную функцию

.

Во-первых, эта функция существует, так как 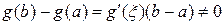по условию теоремы. Далее, она непрерывна на отрезке и дифференцируема на интервале 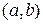, причём её производная равна 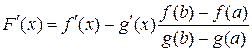. По теореме 23.2(Ролля) существует 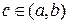такая, что , т.е. , откуда сразу следует заключение теоремы.►

Замечание. Не стоит пытаться «упростить» доказательство теоремы Коши, применяя теорему Лагранжа отдельно к числителю и к знаменателю. Дело в том, что хотя и для существует некоторая точка, обозначим её 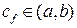, такая, что , и для существует некоторая точка, обозначим её 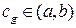, такая, что 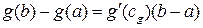, мы не можем сразу утверждать, что эти точки совпадут, т.е.что 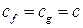. Это равенство следует как раз из приведённого выше доказательства.

Дата добавления: 2015-04-24